The two-photon absorption in ⁸⁵RbF molecules in the radio frequency range was realized for the first time by Hughes and Agraer in 1950.^[1] The method of two-photon Doppler-free spectroscopy was proposed in 1970^[2] and the experiments were carried out by Hansch et al. in 1974.^[3] Two-photon spectroscopy became a powerful tool in measuring hyperfine structure, Stark shifts, and Zeeman splitting for different atoms and molecules. With the optical frequency comb technology, the excitation of two photons offers a platform to study single-photon generation, ^[4] all optical switches, ^[5] quantum logic gates, ^[6] and high precision measurements.^{[7– 10]} The high peak intensity of an ultra-short pulse from a frequency comb laser facilitates frequency conversion via a nonlinear process, which is important for high precision spectroscopy in the wavelength region where continuous wave laser does not reach.^[11] The high resolution two-photon spectrum of Rb confined in the hollow core of a photonic crystal fiber was studied.^[12] Two-photon transition of 5S– 7S in rubidium vapor was realized by using the counter propagating femtosecond pulse.^[13] Spatial and spectral coherence control level for light– matter interaction was significantly enhanced with frequency combs.^[14] The 5P_3/2 → 5D_5/2 hyperfine transition is a promising candidate for a frequency reference at 776  nm because it is narrow and relatively immune to AC-Stark shifts.^[15]

In this paper, a high-precision spectrum of ⁸⁷Rb in a hot atomic vapor is obtained by using two-photon transitions based on an optical frequency comb. The Doppler free excitation is obtained in the region where the counter propagating beams overlap. The two-photon resonance signals with excellent signal-to-noise ratio and lower sensitivity to systematic effects are realized. The temperature and power dependences of the two-photon spectrum are studied. The measurements and predictions are in good agreement with each other.

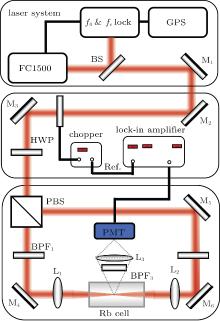
The two-photon transition experimental setup is schematically shown in Fig.  1. The self-referenced femtosecond optical frequency comb system (Menlo systems FC1500) has a repetition frequency of 250  MHz and a pulse width below 150  fs. A broadband frequency comb from 550  nm to 900  nm is generated by using a photonic crystal fiber. Its average power is about 60  mW. Both the repetition rate and the offset frequency are phase locked by controlling the cavity length and the pump power. All synthesizers and counters are calibrated with a global positioning system receiver which has a relative stability better than 5 × 10^{− 12} in 1  s.

In order to enhance the signal-to-noise ratio, the beam is modulated via a chopper (SR540) and the modulated frequency is 200  Hz. The modulated beam is split into two beams with a 50:50 polarizing beam splitting cube. The two beams are filtered by use of different narrowband interference filters to select specific transition and propagate inversely. The counterpropagating beams from the interference filters are then focused inside the ⁸⁷Rb vapor cell. The ⁸⁷Rb vapor cell is 100  mm in length and 25  mm in diameter. The temperature of the vapor cell is controlled by a cylindrical oven that surrounds the vapor cell and is measured by using a thermocouple temperature probe placed at the point in the oven close to the imaged fluorescence region. The vapor cell is placed in a μ -metal shield to reduce the effect of stray magnetic field.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Experimental setup. M: high reflective mirror; HWP: half wave plate; PBS: polarization beam splitter; L: lens; BS: beam splitter; BPF: band pass filter; PMT: photomultiplier; GPS; global positioning system.

The fluorescence is collected by using a 50-mm focal length lens. A 420-nm interference filter with a 10-nm pass band is used to reduce the noises from scattering and ambient light. The photomultiplier tube (Hamamatsu, CR131) output signal is demodulated by a lock-in amplifier (SR830) and then recorded by a computer. The offset frequency of the frequency comb is fixed and the repetition rate is scanned through the synthesizer in steps of 1  Hz per second. Each 1  Hz step the fluorescence is digitized and averaged for 1  s.

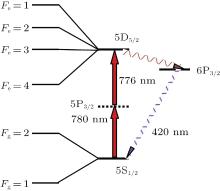
The relevant ⁸⁷Rb atom energy levels 5S_1/2 → 5P_3/2 → 5D_5/2 in this experiment are shown in Fig.  2. ⁸⁷Rb has two hyperfine ground states and several narrowly spaced hyperfine excited states. The ground state of ⁸⁷Rb is split by 6.835  GHz into F = 1 and F = 2 levels. The ⁸⁷Rb atoms of ground state (5S_1/2) are excited to high states (5D_5/2) via two-photon transition. The resonant frequencies of 5S_1/2 → 5P_3/2 transition (780  nm) and 5P_3/2 → 5D_5/2 transition (776  nm) are very nearly commensurate. This leads to the linewidth determined by the width of the 5D_5/2 state. The ⁸⁷Rb atom lifetime of 5D_5/2 state is ∼ 240  ns. The two-photon transition is detected by monitoring the fluorescence at 420  nm due to radiative cascade 5D_5/2 → 6P_3/2 → 5S_{1 /2}.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Relevant hyperfine levels of 87Rb for the 5S1/2 → 5P3/2 → 5D5/2 and 5D5/2 → 6P3/2 → 5S1/2 transitions. The 5S1/2 and 5D5/2 hyperfine structures are inverted.

The optical frequency comb mode can be expressed as f = f₀ + nf_r, where f_r is the pulse repetition rate, f₀ is the carrier envelope offset frequency, and n is an integer of the order of 10⁶. We define the z axis to be the direction of propagation of the beam and v_z is the z component of the atomic velocity. We can write the two-transition resonance condition as^{[16, 17]}

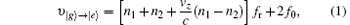
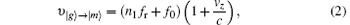
where | g〉 , | m〉 , and | e〉 represent 5S_1/2, 5P_3/2, and 5D_5/2, respectively, n₁ and n₂ are the comb modes. For a given pair of comb modes n₁ and n₂, fix f₀, f_r, and v_z, then the atoms will be effectively excited to the state | e〉 when the resonance conditions are satisfied.

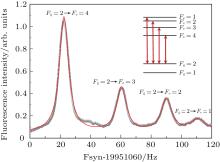
In the experiment, the 420-nm fluorescence signal is collected by using the photomultiplier tube while the repetition frequency of the optical frequency comb scans. The two-photon transition spectrum of ⁸⁷Rb for the 5S_1/2(F_g = 2) → 5D_5/2 (F_e = 4 to 1) transitions are shown in Fig.  3. The fluorescence is plotted as a function of the synthesizer frequency of the optical frequency comb, which has a specific relation with the repetition frequency, that is f_r = f_syn/4+ 245  MHz.

The ratio of intensity of the ground state of ⁸⁷Rb for F_g = 2 to that for F_g = 1 is 5:3. The ratio between intensities for different hyperfine ground state peaks is determined by the statistical weight of the F states in the 5S ground state.^[18] The 5S_1/2 → 5D_J two-photon transition satisfies the selection rule, i.e., | Δ F| ≤ 2. The temperature of the Rb vapor cell is 45  ° C. The scan rate of f_syn is 1  Hz/s, corresponding to an optical frequency scanning speed of about 0.75  MHz/s. The average power of the beam is ∼ 3  mW, whose frequency equals that of the 5S_1/2 → 5P_3/2 transition. Another beam is ∼ 0.7  mW, whose frequency equals that of the 5P_3/2 → 5D_5/2 transition. The dots represent the experimental results and the solid line refers to the Lorentzian fit. The linewidth of two-photon transition 5S_1/2 (F_g = 2) → 5D_3/2 (F_e = 4) is about 5.4  MHz, which is broader than the natural linewidth. This is caused mainly by residual Doppler broadening and transit time broadening. The remaining line-width broadening is related to residual magnetic field, power broadening, and beam misalignment.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Hyperfine two-photon transition spectrum of 87Rb for the 5S1/2(Fg = 2) → 5D5/2 (Fe = 4 to 1) transitions. The dots represent experimental results and the solid line refers to the Lorentzian fit.

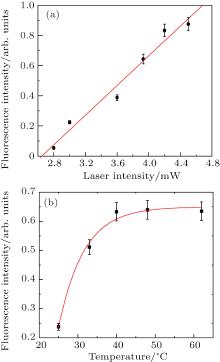
The peak fluorescence intensities of ⁸⁷Rb two-photon spectrum for the 5S_1/2(F_g = 2) → 5D_5/2 (F_e = 4) are measured with different average powers of beam, whose frequency equals that of the 5S_{1/ 2} → 5P_3/2 transition, which are shown in Fig.  4(a). The dots represent the experimental results and the solid line refers to the linear fit. 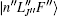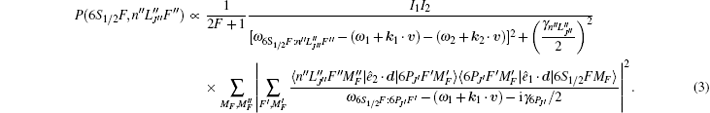The two-photon transition probability P from the 5S_1/2 ground state to a final state is given by second-order perturbation theory as follows:^[19]

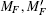
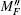
Here, I₁ and I₂ are the intensities of two counterpropagating beams; , and are the projections of the total atomic angular momenta F, F' , and F" along the axis of quantization; ω ₁ and ω ₂ are the frequencies of two counterpropagating photons; v is the velocity of the atom; k₁ and k₂ are the wave vectors for counterpropagating photons; ê ₁₍₂₎ is the unit vector along the direction of the axis of quantization for the first (second) laser beam; d is the electric dipole operator; γ _nL is the homogeneous linewidth of the state | nL_J〉 . From formula  (3), the two-photon transition probability increases with the intensity of two counterpropagating beams, which can be used to qualitatively explain the experimental results.

The temperature dependence of the ⁸⁷Rb two-photon spectrum for the 5S_1/2 (F_g = 2) → 5D_5/2 (F_e = 4) is also studied in this experiment. Figure  4(b) illustrates the peak fluorescence intensities as a function of ⁸⁷Rb vapor cell temperature. The temperature of the Rb vapor cell increases from 21  ° C to 60  ° C. The dots represent the experimental results, and the solid line refers to the exponential fit. We observe a threshold-like behavior along with the peak fluorescence intensity when the temperature of Rb vapor cell exceeds 40 ° C. This result can be explained with self-absorption of the 5P_3/2 → 5S_1/2 fluorescence suppressing an increase in signal.^[20]

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. (a) Fluorescence intensity of 87 Rb spectrum for the 5S1/2(Fg = 2) → 5D5/2 (Fe = 4) as a function of laser average power (corresponding to 5S1/2 → 5P3/2 transition). (b) Fluorescence intensity of 87Rb spectrum for the 5S1/2(Fg = 2) → 5D5/2 (Fe = 4) as a function of temperature of Rb vapor cell. The dots represent experimental results and the solid line refers to fit.

The two-photon transition 5S_1/2 → 5D_5/2 in ⁸⁷Rb is studied by using the optical frequency comb. The high-precision direct frequency comb spectrum is obtained with counterpropagating femtosecond pulses acting on hot ⁸⁷Rb vapor. This technique provides a simple and robust method of obtaining a high-precision spectrum by using a single pulse laser. In the future, a sophisticated pulse-shaping technique will be employed to eliminate the Doppler-broadened background.