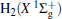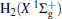†Corresponding author. E-mail: yzsong@sdnu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11304185 and 11074151), China Postdoctoral Science Foundation (Grant No. 2014M561957), the Postdoctoral Innovation Project of Shandong Province, China (Grant No. 201402013), and the Shandong Provincial Natural Science Foundation, China (Grant No. ZR2014AM022).
A globally accurate potential energy surface is reported for the electronic ground-state H2O+. The ab initio energies utilized to map the potential energy surface are calculated at the multireference configuration interaction method employing the aug-cc-pVQZ basis set and the full valence complete active space wave function as reference. In order to improve accuracy of the resulting raw ab initio energies, they are then extrapolated to the complete basis set limit and most importantly to the full configuration-interaction limit by semiempirically correcting the dynamical correlation using the double many-body expansion-scaled external correlation method. The topographical features of the current potential energy surface were examined in detail, which agree nicely with those of other theoretical work.
Due to their importance in planetary ionospheres and interstellar chemistry, ion– molecule reactions have been the subject of a vast amount of studies.[1, 2] From the experimental point of view, since it is quite simple to accelerate ions, molecular beam experiments can be carried out relatively easier on such a kind of reaction over a wide range of relative translational energies. However, it is usually difficult to explore the reaction dynamics studies theoretically on such a kind of reaction system, since the energies of ground and excited potential energy surfaces (PESs) are frequently degenerate or close, and the electronically nonadiabatic processes easily occur.[3– 5] Among a series of ion– molecule reactions, the 
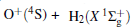
Experimentally, the rate constants for reactions in which a series of positive ions (O+ , N+ , Ar+ , 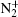
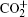
Amongst the vast quantity of theoretical work, employing the quasiclassical trajectory (QCT) approach, Gonzá lez et al.[13, 14] investigated the ion– molecule reaction of O+ (4S) with 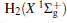
However, the PES constructed by Martí nez et al.[4] was obtained by fitting around 600 ab initio points calculated at CCSD(T) level with cc-pVQZ basis set. We are also aware that the dissociation energy of OH+ (X3∑ − ) was calculated from such PES to be 5.1268 eV, while the experimental value is 5.301 eV, showing a relatively larger difference of 0.1742 eV (∼ 4.0172 kcal· mol− 1). Compared with the most recent result (5.2816 eV) obtained by Paniagua, [5] the difference is calculated to be 0.1544 eV (∼ 3.5606 kcal· mol− 1). Thus, we are motivated to constructing more accurate global analytical PES of H2O+ (X4A″ ) by fitting more accurate ab initio energies to be calculated with multireference configuration interaction (MRCI)[22] level and larger basis set aug-cc-pVQZ[23, 24] (denoted as AVQZ). In this work, a realistic global analytical PES for H2O+ (14A″ ) is reported, which is obtained by fitting 2690 ab initio points that were calculated at MRCI[22] level of theory, using the full valence complete active space (FVCAS)[25] reference wave function and the Dunning' s basis set AVQZ. The resulting ab initio energies have been subsequently corrected, using the double many-body expansion-scaled external correlation (DMBE-SEC)[26] method to extrapolate to the one-electron complete basis set (CBS) limit.[27] The PES so obtained shows the correct behavior at all dissociation channels while providing a realistic representation of the surface features at all interatomic separations.
This paper is organized as follows. Section 2 presents the ab initio calculations employed in the present work. Section 3 describes the analytical representation of the H2O+ (X4A″ ) PES. Main topographical features of the current PES are discussed in Section 4. Finally, Section 5 summarizes the concluding remarks.
In order to map the H2O+ (X4A″ ) PES, a grid of raw 2690 ab initio energies has been calculated, which is defined by 1.2 ≤ RH2/a0 ≤ 3.8, 1.0 ≤ rO+ − H2/a0 ≤ 15.0, and 0.0 ≤ γ /deg ≤ 90 for O+ − H2 channel; while 1.5 ≤ ROH+ /a0 ≤ 4.0, 2.0 ≤ rH− OH+ /a0 ≤ 15.0, and 0.0 ≤ γ /deg ≤ 180 for H− OH+ channel. As described in Ref. [28]– [30], R, r, and γ are the atom– diatom Jacobi coordinates. By using the FVCAS[25] as reference, all ab initio calculations have been carried out at the MRCI[22] level. The AVQZ basis set of Dunning has been employed, with the calculations being performed using the Molpro[31] package. Cs point group symmetry is employed in the ab initio calculation, which holds two irreducible representations, namely, A′ andA″ . For H2O+ (X4A″ ), five A′ and oneA″ symmetry molecular orbitals (MOs) are determined as the active space, amounting to a total of 172 (110A′ + 62A″ ) configuration state functions. The molecular orbitals, which correlate with 2s, 2p atomic orbitals of the O+ ion and the 1s orbital of each H atom, are utilized to determine the valence space. Such a procedure provides a good description of bond formation/breaking which takes place in the reactive process, in which case the CCSD(T) usually fails.
Aiming at accounting for the excitations beyond singles and doubles and, most importantly, for the incompleteness of the basis set, the resulting ab initio energies have subsequently been modeled by scaling the external correlation employing the DMBE-SEC method developed by Varandas.[26] According to the DMBE-SEC scheme, the total energy can be written as the following form
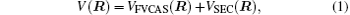
where
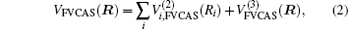
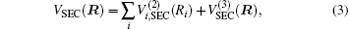
where the first terms of Eqs. (2) and (3) sum over all the diatomic components with i = AB, BC, AC, and R = {RAB, RAC, RBC} in 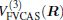

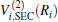
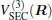
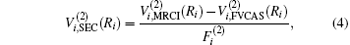
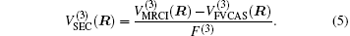
As is done in the previous work, [32– 34] the scaling factors 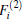
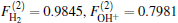
Employing the many-body expansion method proposed by Murrell and Carter, [35] the analytical functional form of H2O+ (X4A″ ) PES can be expressed as

where 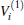

Thus, the one-body term 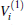
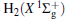
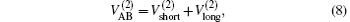
where
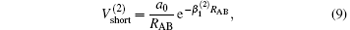
which warrants the diatomic potentials tend to infinite value when RAB→ 0. The long-range potential which tends to zero as RAB→ ∞ takes the following expression .
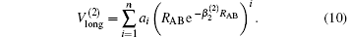
The linear parameters ai (i = 1, 2, … , n) and the nonlinear parameters β i (i = 1, 2) in Eqs. (9) and (10) are obtained by fitting the ab initio potential energies of the diatoms. All the coefficients used to model the diatomic potentials for OH+ (X3∑ − ) and 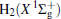
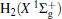
| Table 1. Fitted parameters of two-body energy term in Eq. (10). |
| Table 2. Spectroscopic constants of OH+ and H2 diatoms, with the unit of Re in a.u. (atomic unit), De in unit kcal/mol, and ω e, ω exe, α e, and β e in unit cm− 1. |
By subtracting the two-body energies from the total ab initio energies, for a given triatomic geometry, one can obtain the three-body energies, which are then fitted to the three-body term V(3) written as the M-th order polynomial[36, 37, 39, 40]
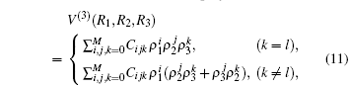
where 
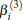
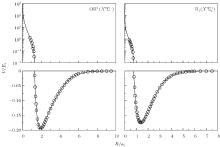 | Fig. 1. Potential energy curves of OH+ (X3∑ − ) and 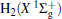 |
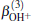
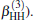
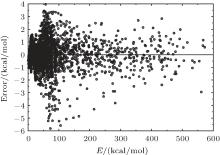
6.99% of the total ab initio energies, which implies that the fitted PES is in good quality.
Table 3 compares the attributes (geometries, energies, and vibrational frequencies) of the relevant stationary points of the current PES with other theoretical results for H2O+ (X4A″ ): C∞ v[OHH]+ , C2v[OH2]+ , and C∞ v[HOH]+ minima, and D∞ v[HOH]+ transition state. Also showing in this table are the results obtained by optimizing at MRCI/AVQZ level of theory in the present work, and at CCSD(T)/cc-pVQZ level of theory by Martí nez et al.[4] As is shown in Table 3, the C∞ v[OHH]+ minimum located at R1 = 2.2950a0 (RH2), R2 = 2.1209a0, and R3= 4.4159a0 (ROH+ ). Comparing with the result calculated from analytical PES of Martí nez et al., [4] the derivations are only 0.0573a0, 0.0336a0, and 0.0237a0, respectively. The well depth calculated from the present PES is 0.2080 Eh relative to the O+ (4S) + H(2S) + H(2S) asymptote, which is 0.006 Eh lower than the results of Martí nez et al., [4] since the present PES is obtained by fitting ab initio energies calculated with higher accuracy, namely MRCI/AVQZ. Comparing with the well depth of the other minima and transition state, the C∞ v[OHH]+ minimum has the lowest energy, which is attributed to the global minimum of H2O+ (X4A″ ). Both the well depth and geometry are in good accordance with the results obtained in the present work through optimization at MRCI/AVQZ level of theory, with the well depth differing by 0.0008 Eh and the maximal difference 0.0789a0 of geometries occurs for OH bond length. The harmonic vibrational frequencies for the C∞ v[OHH]+ minimum obtained by the present PES are 1746.27 cm− 1, 863.03 cm− 1, and 562.55 cm− 1, which are also in good agreement with the results through optimization searches at the MRCI(Q)/AVQZ level (1747.92 cm− 1, 796.11 cm− 1, and 719.09 cm− 1), and the results of analytical PES obtained by Martí nez et al.[4] (1644.09 cm− 1, 785.04 cm− 1, and 765.04 cm− 1).
| Table 3. Properties of stationary points on the fitted H2O+ (X4A″ ) PES a. |
The major topographical features of the H2O+ (X4A″ ) PES reported in the present work are displayed in Figs. 3– 7. The salient features from these contour plots are some of the most relevant stationary points for the title system. Clearly, a smooth and correct behavior can be observed over the whole configuration space. Figure 3 shows a contour plot for the C2v insertion of O+ into H2 diatom from large atom– diatom separations along T-shaped geometries. In this process, when the O+ inserts into H2 diatom, the ∠ HOH opens progressively, while the separation between O+ and the center of H– H shortens, and the bond length of H– H increases. It can be seen from this figure that there exists a local minimum (C2v[OH2]+ ) locating at x ≈ 1.5a0 and y ≈ 3.3a0 (R1 = 1.4945a0, R2 = R3 = 3.4241a0), with the well depth lying at − 0.1954 Eh which is 8.5341 kcal· mol− 1 above the C∞ v[OHH]+ minimum, and the harmonic vibrational frequencies being 1577, 562, and 1886 cm− 1, respectively. The geometry, well depth, and harmonic vibrational frequencies compare well with the results obtained by Martí nez et al.[4] Another notable feature shown in this figure is the D∞ v[HOH]+ transition state lies at R1 = 5.1406a0 and R2 = R3 = 2.7053a0, with the barrier height of − 0.1230 Eh which is 53.338 kcal· mol− 1 above C∞ v[OHH]+ minimum and 44.804 kcal· mol− 1 above the C2 v[OH2]+ minimum. Comparing with the results of Martí nez et al.:[4] the bond length differences are calculated to be 0.0816a0 and 0.0408a0, and the well depth predicted by the current PES is 3.7651 kcal· mol− 1 deeper. The harmonic vibrational frequencies are of D∞ v[HOH]+ transition state are calculated to be 1519.61 cm− 1, 2507.02i cm− 1, and 456.82 cm− 1, with the MRCI/AVQZ results being 1438.66 cm− 1, 3618.64i cm− 1, and 841.35 cm− 1. In turn, the results obtained from the analytical PES by Martí nez et al.[4] are 1204.39 cm− 1, 1759.44i cm− 1, and 675.72 cm− 1, with the CCSD(T)/cc-pvQZ results being 1416.07 cm− 1, 2759.75i cm− 1, and 860.59 cm− 1. As seen from Table 3, the results from the current PES show overall good agreement with the results of Martí nez et al.[4]
Figure 4 shows a contour plot for both OH+ stretching in H– O– H+ linear configuration. The notable features shown in Fig. 4 are the two equivalent asymmetric hydrogen-bonded minima, which are connected by a barrier lying at R2 = R3 = 2.7053a0. Figure 5 shows the contour plot for bond
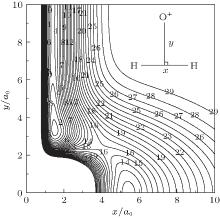 | Fig. 3. Contour plot for C2v insertion of O+ into H2 diatom. Contours equally spaced by 0.0065Eh, starting at − 0.192Eh. |
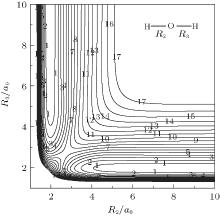 | Fig. 4. Contour plot for bond stretching in [H– O– H]+ linear configuration. Contours equally spaced by 0.004Eh, starting at − 0.1158Eh. |
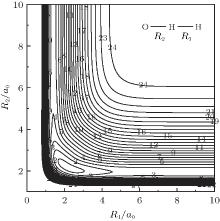 | Fig. 5. Contour plot for bond stretching in [O– H– H]+ collinear configuration. Contours equally spaced by 0.0085Eh, starting at − 0.205Eh. |
stretching of OH+ and HH in O– H– H+ collinear configuration. A minimum can be seen to locate at R1 = 2.2950a0, and R2 = 2.1209a0, which is attributed to be the C∞ v[OHH]+ minimum. Also visible in this figure is O+ can approach HH diatom via a barrierless process from large atom– diatom separations along the O– H– H+ collinear configurations, thus agreeing with findings of Martí nez et al.[4]
Figure 6 shows a contour plot for an H atom moving around an OH+ diatom with the bond length of OH+ fixed at equilibrium geometry ROH+ = 1.943a0, which lies along the X axis with the center of the bond fixed at the origin. One of the salient features is the C∞ v[OHH]+ minimum exists when H approaches OH+ collinearly, which can also be seen in Fig. 5. In turn, figure 7 shows a contour plot for O+ atom moving around a fixed HH diatom with the bond length fixed at equilibrium geometry RHH = 1.401a0, which lies along the X axis
with the center of the bond fixed at the origin. As can be seen in this figure, there exist a C2v and two equivalent C∞ v minima in the process of O+ moving around the fixed HH diatom. Also shown in Figs. 6 and 7 are the ab initio energies utilized in the fitting procedure, which cover both the short and long regions, warranting the reliable behavior of the current PES. These two contour plots clearly reveal a smooth behavior both at short and at long-range regions.
A wealth of accurate MRCI/AVQZ energies have been calculated in the present work to map the PES of H2O+ (X4A″ ). The resulting raw energies have been corrected subsequently using the DMBE-SEC method and then utilized in the fitting procedure to obtain the globally accurate PES, which is expected to be realistic over the entire configuration space. The various topographical features of the current PES have been examined in detail and compared with the previous theoretical results. The properties of several minima and transition states, including the geometries, energies, and vibrational frequencies, have been characterized on the current H2O+ (X4A″ ) PES, which agree nicely with the topographical predictions of other theoretical work. Based on such features, it is concluded that the PES here reported is globally valid while accurately fitting the ab initio points utilized for its calibration. Thus, the present H2O+ (X4A″ ) PES should be valuable for studying the kinetics and dynamics of reactions involving ground-state H2O+ , such as 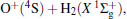
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|