†Corresponding author. E-mail: chengxt02@gmail.com
*Project supported by the National Natural Science Foundation of China (Grant No. 51376101) and the Science Fund for Creative Research Groups, China (Grant No. 51321002).
Taking the output power, thermal efficiency, and thermo-economic performance as the optimization objectives, we optimize the operation parameters of a thermodynamic system with combined endoreversible Carnot heat engines in this paper. The applicabilities of the entropy generation minimization and entransy theory to the optimizations are discussed. For the discussed cases, only the entransy loss coefficient is always agreeable to the optimization of thermal efficiency. The applicabilities of the other discussed concepts to the optimizations are conditional. Different concepts and principles are needed for different optimization objectives, and the optimization principles have their application preconditions. When the preconditions are not satisfied, the principles may be not applicable.
The optimizations of thermodynamic systems are very important for the reduction of energy utilization and cost. In different practical application cases, there are different optimization objectives, such as the coefficient of performance (COP), [1, 2] output power, [3, 4] thermal efficiency, [3, 4] thermo-economic performance, [5, 6] etc. In engineering, the operation parameters of the thermodynamic system should be optimized to maximize the corresponding optimization objectives.[7– 9] In recent decades, some theories have been developed and applied to the optimizations, such as the entropy generation minimization, [1, 2, 4, 10, 11] exergy destruction minimization, [12] finite time thermodynamics, [13] and entransy theory.[2, 4, 14]
The concepts of entropy generation and exergy destruction are widely applied to the analyses and optimizations of thermodynamic systems[1, 2, 4, 10– 12, 15, 16] because they can describe the process irreversibility and the minimizations of the irreversibility can increase the system performance. As the entropy generation can describe the exergy loss, [17] the entropy generation minimization is equivalent to the exergy destruction minimization when the environment temperature is fixed.[18] However, when the output power was the optimization objective, it was found that neither the entropy generation minimization nor the exergy destruction minimization always leads to the largest output power.[4, 15, 16] When the thermal efficiency was the objective, it was also shown that the entropy generation minimization does not always result in the largest thermal efficiency.[4] In addition, there are not many reports on the applicability of entropy generation minimization to the optimization of thermo-economic performance.
For the entransy theory, it was developed for heat transfer analyses and optimizations.[19– 28] Cheng and Liang[2, 4, 15] extended this theory to the analyses and optimizations of thermodynamic systems. Applications of the entransy theory to thermodynamic systems can be found in Refs. [2], [4], [15], [18], [29]– [32]. Under some conditions, the concepts of entransy loss and entransy loss coefficient are effective for the optimizations of output power and thermal efficiency, [2, 4, 15, 18, 29, 30, 32] respectively. However, it was also shown that larger entransy loss does not always lead to larger output power.[33] Furthermore, there is still no report on the applicability of entransy theory to the optimization of thermo-economic performance.
From the above discussion, it can be seen that the applicabilities of the entropy generation minimization, exergy destruction minimization and entransy theory to the optimizations of thermodynamic systems need further investigations. Taking the output power, thermal efficiency and thermo-economic performance as the objectives, we optimize the operation parameters of the thermodynamic system with combined endoreversible Carnot heat engines, [3] in which the heat released by the first Carnot heat engine enters the second Carnot heat engine to do work. We discuss the applicabilities of the theories to the optimizations. As the entropy generation minimization and exergy destruction minimization are equivalent, the exergy destruction minimization is not discussed in this paper.
The discussed system is shown in Fig. 1. In the system, the high and low temperatures of the working medium in the first endoreversible Carnot heat engine are T1 and T2, while those of the working medium in the second endoreversible Carnot heat engine are T3 and T4, respectively. The flow rate of heat absorbed from the high temperature heat source at temperature TH by the working medium of the first endoreversible Carnot heat engine is QH, while those released to the second endoreversible Carnot heat engine and low temperature heat source at temperature TL are Qm and QL, respectively. The output power of the first endoreversible Carnot heat engine is W1, while that of the second one is W2. The heat flow rates, QH, Qm, and QL, satisfy

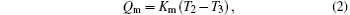
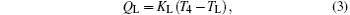
where KH is the product of the heat transfer area and corresponding heat transfer coefficient between TH and T1, Km is that of the heat transfer area and corresponding heat transfer coefficient between T2 and T3, and KL is that of the heat transfer area and corresponding heat transfer coefficient between T4 and TL.
The total output power of the system is
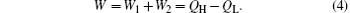
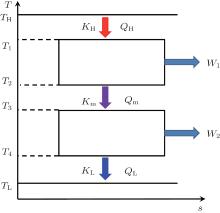 | Fig. 1. Thermodynamic system with combined endoreversible Carnot heat engines.[3] |
In the two endoreversible Carnot heat engines, we have

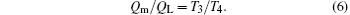
The thermal efficiency of the system is

Sometimes, the economic cost is the main objective that we should consider. The thermo-economic performance of the system can be evaluated by[6]
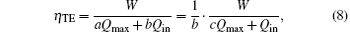
where Qmax is the maximum heat flow that the heat engine can afford, Qin is the practical heat flow rate into the system, and a and b are the coefficients, and c is the ratio of a to b. In Eq. (8), aQmax expresses the economic cost from the size and material of the heat engine, and bQin expresses that from the practical operation parameters. Then, the denominator can be treated as the economic cost, and equation (8) is the output power per unit economic cost. In Fig. 1, Qin equals QH. So, with Eq. (8), we have

In a certain case, Qmax should be a definite value. So, the thermo-economic performance has the same variation tendency as that of the thermal efficiency when QH is given. The relationship between the thermo-economic performance and thermal efficiency has been obtained.
If we analyze the system with the entropy generation minimization, the entropy generation rate of the system can be calculated by


It can be seen that smaller entropy generation rate leads to larger output power with fixed thermodynamic forces of the heat sources, 1/TL and 1/TH, and heat flow rate into the system, QH. Equation (11) indicates the relationship between the entropy generation rate and output power.
Furthermore, the entropy generation numbers[4, 34] can also be obtained as follows:
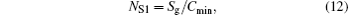
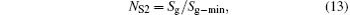
where Cmin is the minimum heat capacity flow rate in the discussed system, and Sg− min is the minimum entropy generation rate. For any thermodynamic system, both Cmin and Sg− min are definite values. Therefore, the variation tendencies of the entropy generation numbers are the same as that of the entropy generation rate.
On the other hand, if we analyze the system with the entransy theory, the entransy loss rate can be calculated by
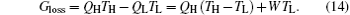
Here, the relationship between the entransy loss rate and output power is clear. The entransy loss coefficient is defined as[4, 33]
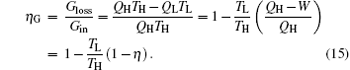
It can be seen that larger entransy loss coefficient leads to larger thermal efficiency for fixed ratio of TL to TH. With this equation, the direct relationship between the thermal efficiency and entransy loss coefficient has been set up.
For any thermodynamic system, there are different optimization objectives in engineering, such as the maximum output power, the largest thermal efficiency, the best thermo-economic performance, etc. The system in Fig. 1 will be optimized with different objectives below. The applicabilities of the entropy generation minimization and entransy theory to the optimizations will also be discussed.
For the system in Fig. 1, we can analyze some numerical cases in this section. As the variation tendencies of the entropy generation numbers are the same as that of the entropy generation rate, we only calculate the entropy generation rate below.
First, assume that TH = 450 K, TL = 300 K, c = 2, and QH = 1000 W. In the system, Qmax results in the cost from the size and material of the system when we design the system. As QH is fixed in this case, we assume that Qmax equals QH to reduce the cost of the system. Furthermore, we assume that KH, Km, and KL satisfy

and the value of K is 300 W/K. For different values of KH, Km, and KL, the output power can be obtained from Eqs. (1)– (6) and shown in Fig. 2(a). It can be seen that the maximum output power, 285.7 W, can be obtained when KH = Km = KL = 100 W/K. For the thermal efficiency and thermo-economic performance, equations (7) and (9) show that their variation tendencies are the same as that of the output power because QH is fixed and Qmax equals QH. Therefore, both the thermal efficiency and thermo-economic performance reach their maximum values when KH = Km = KL = 100 W/K.
 | Fig. 2. Variations of the output power (a), entropy generation rate (b), and entransy loss rate (c) with different values of KH, Km, and KL when QH is fixed. |
The variations of the entropy generation rate and entransy loss rate are shown in Figs. 2(b) and 2(c), respectively. The numerical results show that the entropy generation rate obtains its minimum value, 0.159 W/K, when KH = Km = KL = 100 W/K. At the same time, the entransy loss rate reaches its maximum value, 2.36× 105 W· K. As QH and TH are both fixed, the three discussed optimization objectives have the same variation tendencies, and equation (15) shows that the variation tendency of the entransy loss coefficient is the same as that of the entransy loss rate. Considering Eqs. (10)– (15), we can conclude that the minimum values of the entropy generation rate and entropy generation numbers and the maximum values of the entransy loss rate and entransy loss coefficient all lead to the maximum values of the output power, thermal efficiency, and thermo-economic performance in this case.
In this case, TH, TL, and QH are all fixed, so the heat flow rate from the high temperature heat source and the thermodynamic forces of the high and low temperature heat sources, 1/TH and 1/TL, are all given. The preconditions[35] under which the entropy generation minimization can be used to maximize the output power of the system are all satisfied. At the same time, the preconditions[35] under which the maximum entransy loss rate leads to the maximum output power are also satisfied. This is the reason why both the entropy generation minimization and the entransy loss maximization lead to the largest output power.
Furthermore, as QH is given in this special case, the maximum output power, thermal efficiency, and thermo-economic performance are obtained at the same time. This is the reason why the entropy generation minimization and entransy loss maximization also result in the maximum values of the thermal efficiency and thermo-economic performance in this case.
In the second case, QH is not fixed. We assume that TH = 450 K, TL = 300 K, T1 = 435 K, c = 2, and K = 300 W/K. For this case, the variations of the output power, thermal efficiency, and thermo-economic performance with different values of KH, Km, and KL are shown in Fig. 3. The numerical results show that the output power reaches its maximum value when Km = KL = 79 W/K, the thermo-economic performance arrives at its maximum value when Km = KL = 84 W/K, and the thermal efficiency increases with increasing Km and KL. The variations of the entropy generation rate, and entransy loss rate are shown in Figs. 4(a) and 4(b). It can be seen that neither the entropy generation minimization nor the entransy loss maximization leads to the maximum output power.
 | Fig. 3. Variations of the output power (a), thermal efficiency (b), and thermo-economic performance (c) with different values of KH, Km, and KL when T1 is fixed. |
 | Fig. 4. Variations of the entropy generation rate (a), entransy loss rate (b), and entransy loss coefficient (c) with different values of KH, Km, and KL when T1 is fixed. |
When the thermal efficiency is the optimization objective, the numerical results in Fig. 2(c) and Eq. (15) show that larger entransy loss coefficient always corresponds to larger thermal efficiency for fixed ratio of TL to TH. As both values of TL and TH are given, it is very clear that the entransy loss coefficient maximization can be used to optimize the thermal efficiency. It can also be found that smaller values of entropy generation rate, and entropy generation numbers still result in larger thermal efficiency.
When we calculate the thermo-economic performance, we assume that Qmax is the maximum QH in our calculation. In Figs. 3 and 4, the numerical results show that neither the entropy generation minimization nor the entransy loss maximization is applicable for the optimization of the thermo-economic performance.
In this case, Qmax does not always equal QH, so the differences between different optimization objectives can be found. The thermo-economic performance cannot be evaluated by the entropy generation minimization or the entransy theory any more. As QH is not given, the application preconditions[35] for the entropy generation and entransy loss maximization are not satisfied. Then, the maximum value of the entransy loss rate, the minimum values of the entropy generation rate, and entropy generation numbers do not correspond to the maximum output power in this case. Only the thermal efficiency is still agreeable to the entropy generation minimization and entransy loss coefficient maximization.
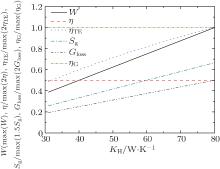
In the third case, TH = 450 K, T1 = 435 K, T2 = 400 K, T3 = 380 K, T4 = 330 K, TL = 300 K, and c = 2. When the thermo-economic performance is analyzed, we also assume that Qmax is also the maximum QH in our calculation. In this case, the values of Km and KL can be calculated for any value of KH because the working temperatures of the working mediums are given. The variations of the output power, thermal efficiency, thermo-economic performance, entropy generation rate, entransy loss rate, and entransy loss coefficient with KH can be obtained and shown in Fig. 5. The results show that the output power, thermo-economic performance, entropy generation rate, and entransy loss rate all increase with increasing KH, while the thermal efficiency and entransy loss coefficient both stay constant.
As the working temperatures of the working mediums are fixed, we can find that the thermal efficiency is also a fixed value from Eqs. (5) and (6). Therefore, equation (9) can be rewritten as
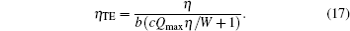
The variation tendency of the thermo-economic performance is the same as that of the output power in this case. This is the reason why both the output power and thermo-economic performance increase with increasing KH.
If the output power or thermo-economic performance is the optimization objective, it can be seen that the entransy loss maximization is still applicable for this case, while the entropy generation minimization is not. The thermal efficiency is a definite value if the working temperatures of the working mediums are fixed, and only the entransy loss coefficient can describe the thermal efficiency in this case.
In the optimization cases above, it can also be seen that we need different optimization concepts and principles for different optimization objectives. Each optimization principle has its specific application precondition.[36] When the precondition is not satisfied, the principle may be not applicable. The discussed theories have their limitations too. In the discussed cases, only the entransy loss coefficient is always applicable for the optimization of thermal efficiency. For optimizing the output power and thermo-economic performance, neither the entropy generation minimization nor the entransy theory is applicable for all cases.
Taking the output power, thermal efficiency, and thermo-economic performance as the optimization objectives, the combined endoreversible Carnot heat engines with fixed high and low temperatures of heat sources are discussed for three numerical cases. The optimal operation parameters that lead to the maximum values of the corresponding optimization objectives are obtained.
Different optimization concepts and principles are needed for different optimization objectives. Both the entropy generation minimization and entransy theory have their application preconditions. When the preconditions are satisfied, the theories are applicable for the corresponding optimizations, otherwise, the theories may be not applicable. Neither of the theories is universal, and they both have their limitations. We should pay attention to their application preconditions when we use them to optimize thermodynamic systems.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|