†Corresponding author. E-mail: mikeshujian@jxufe.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 61462033).
Three-party password-based key agreement protocols allow two users to authenticate each other via a public channel and establish a session key with the aid of a trusted server. Recently, Farash et al. [Farash M S, Attari M A 2014 “An efficient and provably secure three-party password-based authenticated key exchange protocol based on Chebyshev chaotic maps”, Nonlinear Dynamics77(7): 399–411] proposed a three-party key agreement protocol by using the extended chaotic maps. They claimed that their protocol could achieve strong security. In the present paper, we analyze Farash et al.’s protocol and point out that this protocol is vulnerable to off-line password guessing attack and suffers communication burden. To handle the issue, we propose an efficient three-party password-based key agreement protocol using extended chaotic maps, which uses neither symmetric cryptosystems nor the server’s public key. Compared with the relevant schemes, our protocol provides better performance in terms of computation and communication. Therefore, it is suitable for practical applications.
Characterized by sensitive reliance on initial conditions, unpredictability, pseudo-randomness, and ergodicity, the chaotic system can be used to design a cryptosystem. Over the past decades, the secret key system based on chaos theory has been studied widely to be applied as hash functions, [1, 2] symmetric encryption schemes, [3– 5] and stream ciphers.[6, 7]
In recent years, the chaotic map has also been used to design public encryption schemes and key agreement protocols. The key agreement protocol is one of the most important cryptography mechanisms since it allows parties to authenticate each other and establish a shared secret key for the subsequent communication. In 1976, Diffie and Hellman first proposed a key agreement protocol.[8] According to the modular exponentiation operation or scalar multiplication operation on elliptic curves, researchers have proposed many key agreement protocols for different applications.[9– 13] As the theory and application of chaos develop significantly, chaos has become a promising candidate in the field of cryptography. Therefore, it is of practical significance to design efficient and secure key agreement protocols using the chaotic maps.
According to a chaotic public key cryptosystem, Xiao et al. first proposed a key agreement protocol in 2007.[14] Unfortunately, Han demonstrated that their protocol is not secure.[15] Xiang also pointed out that Xiao et al.’ s protocol suffers the off-line password guessing attack.[16] On the basis of a chaotic map, Tseng et al. proposed a key agreement protocol that preserves user anonymity.[17] However, Niu and Wang pointed out that Tseng et al.’ s protocol cannot withstand an insider attack, and cannot provide the perfect forward security either.[18] To solve the problems, Niu and Wang proposed an improved scheme.[18] However, Yoon pointed out that Niu and Wang’ s protocol cannot resist the denial of service attack.[19] According to Tseng et al.’ s protocol, Xue and Hong presented a chaotic map-based key agreement protocol.[20] However, Tan demonstrated that Xue and Hong’ s protocol is vulnerable to the man-in-the-middle attack.[21] Based on the extended chaotic map, Lee et al. proposed an anonymous key agreement protocol.[22] Unfortunately, He et al. pointed out that Lee et al.’ s protocol cannot resist the denial of service attack.[23] In 2014, Shu proposed a secure chaotic maps-based key agreement protocol without smart cards.[24] The protocols mentioned above were designed in the client-server environment.[14– 24] For large-scale server– server or client– client environments, these protocols are inconvenient since each participant has to remember different passwords for the intended peer. The shared password will cause the key management problems. To handle this issue, many key agreement protocols in three-party settings have been developed.[25– 32] In a three-party key agreement protocol, two users can authenticate each other and establish a session key with the aid of a trusted server. In this way, each user only needs to remember a password with the server, which eliminates the key management problems.
In 2012, Lai et al. first presented a three-party key agreement protocol by using the extended chaotic map.[25] Later, Zhao et al. pointed out that Lai et al.’ s protocol cannot withstand the off-line password guessing attack.[26] To overcome the weakness, Zhao et al. also proposed an improved protocol.[26] Smart cards are required in both Lai et al.’ s and Zhao et al.’ s protocols to store secret information. However, tamper-resistant card readers are not available everywhere.[32] In such an environment, it is unpractical to design a key agreement protocol with smart cards. To handle this issue, many three-party chaotic maps-based key agreement protocols without smart cards have been developed.[27– 30] These protocols made use of the server’ s public key to achieve strong security. However, employing the server’ s public key is a burden to the users, because they have to store the public key and verify it in advance. Recently, Farash and Attari proposed a three-party chaotic maps-based key agreement protocol without smart cards, [31] which used neither symmetric cryptosystems nor the server’ s public key. They claimed that their protocol could withstand various attacks. We investigate the security of their protocol and show that it is vulnerable to the off-line password guessing attack. To solve the problem, we propose a new key agreement protocol.
The rest of this paper is organized as follows. In Section 2, the Chebyshev chaotic map is defined and some properties of it are discussed. In Section 3, the Farash et al.’ s protocol is reviewed, and its security is analyzed. We propose a new three-party key agreement in Section 4. Security analysis and performance analysis of our protocol are given in Section 5 and Section 6 respectively. Finally, some conclusions are drawn in Section 7.
In this section, we will review the Chebyshev chaotic map and some hard problems based on it.
Definition 1 Let n be an integer and x be a variable taking values over the interval [− 1, 1]. The Chebyshev polynomial map Tn : R → R is defined by the following recursive relation:
Tn(x) = 2xTn– 1(x) – Tn− 2(x), n ≥ 2, where T0(x) = 1 and T1(x) = x.
Definition 2 The Chebyshev polynomial achieves the semi-group property:

Obviously, the Chebyshev polynomial satisfies the commutative property under composition. Thus, Tr (Ts(x)) = Ts (Tr(x)).
To avoid the periodicity of the cosine function, Zhang extended the interval (− 1, 1) to (− ∞ , + ∞ ) and proved that the semi-group property still holds for the Chebyshev polynomial defined in the interval (− ∞ , + ∞ ), [33] which can be defined as follows:
Tn(x) = 2xTn– 1(x) − Tn− 2(x)mod P, where n ≥ 2, x ∈ (− ∞ , + ∞ ), and P is a large prime number.
The extended Chebyshev polynomial also satisfies the commutative property under composition.
Moreover, three problems about the extended Chebyshev polynomial are assumed to be intractable within polynomial time.
Definition 3 Discrete logarithm (DL) problem: Given three elements x ∈ (− ∞ , + ∞ ), y ∈ Zn and P that is a large prime number, the task of the discrete logarithm problem (DLP) is to find an integer r which satisfies y = Tr(x)modP.
Definition 4 Computational Diffie– Hellman (CDH) problem: P is a large prime number, given three elements x ∈ (− ∞ , + ∞ ), Tr(x)modP, Ts(x)modP, the task of the computational Diffie– Hellman problem (CDHP) is to compute Trs(x)modP without knowing values r and s.
Definition 5 Decisional Diffie– Hellman (DDH) problem: P is a large prime number, given four elements x ∈ (− ∞ , + ∞ ), Tr(x)modP, Ts(x)modP, and Tω (x)modP, the task of the decisional Diffie– Hellman problem (DDHP) is to determine whether Trs(x) and Tω (x) are equal without knowing values r, s, and ω .
In this section, we review Farash et al.’ s protocol based on an extended chaotic map. The notations used throughout the paper are summarized in Table 1.
| Table 1. Notations used in this article. |
There are three phases in the Farash et al.’ s protocol, i.e., system setup phase, registration phase, and authentication phase.
The server S selects the following parameters: (i) A large prime number P, (ii) a ∈ ZP, (iii) The hash function H() and H1(), (iv) Choose randomly an integer s ∈ [1, P+ 1] as the long-term secret key.
S publishes the parameters {P, a, H(), H1()} and keeps the secret key s.
When a user wants to be a legal user, the following steps will be executed between the user and the server through a secure channel: i) the user chooses an easy-to-remember password pwi and an identity IDi, computes PWi = Tpwi(a)modP, then sends (IDi, PWi) to the server. ii) the server computes VPWi = H(IDi, s) + PWimodP, and stores (IDi, VPWi) in its database.
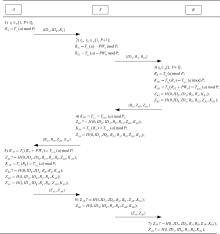
As shown in Fig. 1, the following steps will be executed when the users A and B want to authenticate each other with the aid of the server S.
1) A chooses rA ∈ [1, P + 1] and computes RA = TrA (a)modP, then sends (IDA, IDB, RA) to S.
2) Upon receiving the messages (IDA, IDB, RA), S generates two random numbers rS1, rS2 ∈ [1, P + 1], computes RS1 = Trs1(a) − PWA mod P and RS2 = Trs2(a) − PWB mod P, sends (IDA, RA, RS2) to B.
3) B generates a random number rB ∈ [1, P + 1], computes RB = TrB(a) mod P, KBA = TrB(RA) = TrB rB(a) mod P, KBS = TrB(RS2 + PWB) = TrBrS2(a) mod P, ZBA = H(0, IDB, IDA, RB, RA, KBA) and
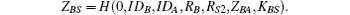
Then, B sends (RB, ZBS, ZBA) to S.
4) Upon receiving the messages (RB, ZBS, ZBA), S computes KSB = TrS2 = TrBrS2(a) mod P and checks whether ZBS and H(0, IDB, IDA, RB, RS2, ZBA, KSB) are equal. If it holds, S computes KSA = TrS1(RA) = TrS1rA(a) mod P and
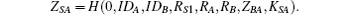
S sends (RS1, RB, ZBA, ZSA) to A.
5) A computes KAS = TrA(RS1 + PWA) = TrArS1(a) mod P and checks whether ZSA and
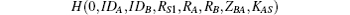
are equal. If it holds, A computes
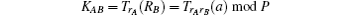
and checks whether ZBA and H(0, IDB, IDA, RB, RA, KAB) are equal. If it holds, A computes ZAB = H(1, IDA, IDB, RA, RB, KAB) and ZAS = H(1, IDA, IDB, RA, RS1, ZAB, KAS). A sends (ZAS, ZAB) to S and computes the session key
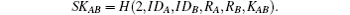
6) S checks whether ZAS and H(1, IDA, IDB, RA, RS1, ZAB, KSA) are equal. If it holds, S computes ZSB = H(1, IDA, IDB, RA, RB, ZAB, KSB) and sends (ZAB, ZSB) to B.
7) B checks whether ZSB and H(1, IDA, IDB, RA, RB, ZAB, KBS) are equal, and checks whether ZAB and H(1, IDA, IDB, RA, RB, KBA) are equal. If they both hold, A is authenticated. B computes the session key SKBA = H(2, IDA, IDB, RA, RB, KBA).
Farash et al. claimed that their protocol could resist various attacks. Unfortunately, we will demonstrate that their protocol is vulnerable to the off-line password guessing attack. Since Farash et al.’ s protocol was executed in the public network, then we could assume that the adversary Φ has total control over the communication between the server and the users in the authentication phase. Φ may eavesdrop, intercept, insert, modify, or delete any messages in the channel. Through the following steps, Φ could extract the password of the user A.
3.2a) At first, the adversary Φ masquerades as the legal user A. Φ chooses r ∈ [1, P + 1] and computes RA = Tr(a)modP, then sends (IDA, IDB, RA) to S.
3.2b) Φ intercepts the messages (RS1, RB, ZBA, ZSA) sent by S, where RS1 = Trs1(a) − PWA mod P.
3.2c) Φ guesses a password pw, and computes
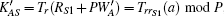
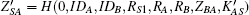
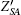
In this section, we propose a new three-party key agreement protocol by using extended chaotic maps. Our protocol consists of three phases, i.e., system setup phase, registration phase, and authentication phase.
The server S selects the following parameters:
4.1a) a large prime number P,
4.1b) x ∈ ZP,
4.1c) the hash function H(),
4.1d) choose randomly an integer s ∈ [1, P + 1] as the long-term secret key.
S publishes the parameters {P, x, H()} and keeps the secret key s.
When a user wants to be a legal user, the following steps will be executed between the user and the server through a secure channel.
Step 1 The user chooses an easy-to-remember password pwi and an identity IDi, computes PWi = Tpwi(x)modP, then forwards (IDi, PWi) to the server.
Step 2 The server computes VPWi = H(IDi, s) + PWi modP, and stores (IDi, VPWi) in its database.
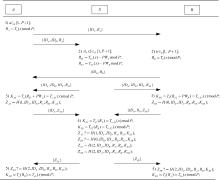
As shown in Fig. 2, the following steps will be executed when the users A and B want to authenticate each other with the aid of the server.
1) A chooses a random a ∈ [1, P + 1] and computes RA = Ta(x)mod P, then sends (IDA, RA) and (IDA, IDB, RA) to B and S respectively.
2) Upon receiving the messages (IDA, RA), B chooses a random b ∈ [1, P + 1] and computes RB = Tb(x)modP, then sends (IDB, RB) to A. Upon receiving the messages (IDA, IDB, RA), S computes PWA = VPWA– H(IDA, s) and PWB = VPWB– H(IDB, s). S generates two random numbers S1, S2 ∈ [1, P + 1], computes RS1 = TS1(x) − PWA mod P and RS2 = TS2(x) − PWB mod P, then sends (IDA, IDB, IDS, RS1) and (IDA, IDB, IDS, RS2) to A and B respectively.
3) Upon receiving the messages (IDB, RB) and (IDA, IDB, IDS, RS1), A computes KAS = Ta(RS1 + PWA) = Ta· S1(x) mod P and ZAS = H(1, IDA, IDB, RA, RS1, KAS), then sends (IDA, ZAS) to S. Upon receiving the messages (IDA, IDB, IDS, RS2), B computes KBS = Tb (RS2 + PWB) = Tb· S1(x) mod P and ZBS = H(0, IDB, IDA, RB, RS2, KBS), then sends (IDB, RB, ZBS) to S.
4) Upon receiving the messages (IDA, ZAS) and (IDB, RB, ZBS) which are sent by A and B respectively, S computes KSA = TS1(RA) = Ta· S1(x) mod P, KSB = TS2(RB) = Tb· S2(x) mod P. S checks whether ZAS and H(1, IDA, IDB, RA, RS1, KSA) are equal, and checks whether ZBS and H(0, IDB, IDA, RB, RS2, KSB) are equal. If they both hold, S computes ZSA = H(2, IDA, IDB, RA, RB, KSA) and ZSB = H(2, IDA, IDB, RA, RB, KSB), then sends (ZSA) and (ZSB) to A and B respectively.
5) Upon receiving ZSA, A checks whether ZSA and H(2, IDA, IDB, RA, RB, KAS) are equal. If it holds, A computes the session key SKAB = H(3, IDA, IDB, RA, RB, KAB), where KAB = Ta (RB) = Tab(x) mod P. Upon receiving ZSB, B checks whether ZSB and H(2, IDA, IDB, RA, RB, KBS) are equal. If it holds, B computes the session key SKBA = H(3, IDA, IDB, RA, RB, KBA), where KBA = Tb(RA) = Tba(x) mod P.
It is clear that SKAB = SKBA.
In this section, we analyze the proposed protocol in terms of security requirements and functional requirements.
In this subsection, we briefly review the security model proposed by Abdalla and Pointcheal.[34] A three-party key agreement protocol Π which consists of two types of participants, a client U, and a trusted server S. During the execution of a protocol, each of the participants may have several instances. The i-th instance of U (resp. S) is denoted by 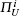
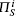
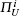


In the model, the adversary Φ is assumed to control the communication network. Φ interacts with the participants through a bounded number of queries which model the capabilities of the adversary in an actual attack. These queries are as follows.
Execute (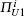

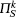
SendClient (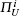
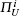
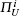
SendServer (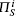


Reveal (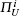
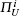
Corrupt (U): This query returns the password of the client U.
Test (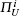
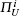
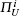
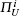
Definition 6 Two instances 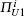

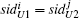
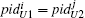
Definition 7 An instance 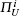
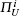
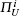
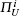
Definition 8 Let succ(Φ ) denote the event that Φ asks a single test query to some fresh 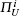
Theorem 1 Assume that hash function H is modeled as random oracles. Let D be the small password dictionary. Let Π describe the protocol defined in Fig. 2. Suppose that DDH assumption holds, then
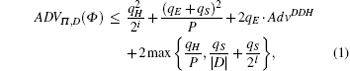
where qH, qE, and qS represent the number of hash queries, execute queries and send queries.
We define a sequence game Gi (0 ≤ i ≤ 4) starting with an actual attack game G0 and ending up with game G4 where the adversary has no advantage. We define an event Succi that Φ correctly guesses the bit b in the test session.
Game G0 : The simulation of this game is the same as the real attack in the random oracle model, we do not modify the simulation of the oracles. Thus, we have
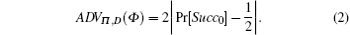
Game G1 : In this game, we simulate the hash oracle H by maintaining a hash 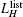

Game G2 : The simulation of this game is identical with G1 except that it will be terminated if a collision appears in the simulation of the partial transcripts (RA, RS1) or (RB, RS2) and the hash values. According to the birthday attack, the probability of collisions of the simulation of H oracle is at most 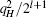
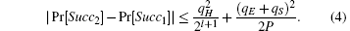
Game G3 : In this game, we change the simulation of SendClient query. At first, we randomly select partner instance 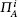
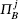
– On a query SendClient (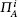
– On a query SendClient(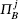
– On a query SendClient(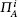
– On a query SendClient(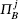
It is easy to see that this game is indistinguishable from game G2. Then we have
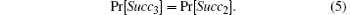
Game G4 : In this game, we once again change the simulation of SendClient query. At first, we obtain a DDH tuple (Ta(x), Tb(x), W) without knowing values a and b.
– On a query SendClient(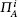
– On a query SendClient(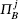
– On a query SendClient(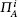
– On a query SendClient(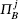
– On a query SendClient(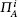
– On a query SendClient(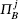
The probability that the adversary Φ picks the selected session as the test session is 1/qE. Following the above simulation, in the case of W = Tab(x), this environment for the adversary is equivalent to G3. Otherwise, this environment for the adversary is equivalent to G4. Finally, if the adversary believes that he interacted with G3, then we can determine that W = Tab(x). If the adversary believes that he interacted with G4, then we can determine that W ≠ Tab(x). Then we have
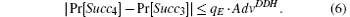
In game G4, there are three possible ways that the adversary Φ can distinguish the real session key and the random number.
Case 1: Φ makes hash query on H(3, IDA, IDB, RA, RB, W). The probability that this event occurs is qH/P.
Case 2: The corrupt(UB) query has been made, which implies that the corrupt(UA) query has not been made. Suppose that the adversary Φ tries to communicate with other participants on behalf of client A. Φ has to obtain the password of client A and compute valid message ZAS. The probability of Φ launching the on-line password guessing attack is qS/D. The probability for Φ to compute the valid message ZAS is qS/P. Therefore, the probability for this event to occur is qS/| D| + qS/2l.
Case 3: The corrupt(UA) query has been made, which implies that the corrupt(UB) query has not been made. Like Case 1, the probability for this event to occur is qS/| D| + qS/2l.
Therefore, we have
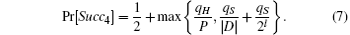
In this subsection, we will analyze the proposed protocol and show that it could withstand various known attacks.
In our protocol, the time stamps are not used to resist the replay attack. Due to the freshness of the ephemeral key and no leakage of the participants’ password, the replayed messages that the adversary Φ has intercepted some communication data before will not pass the verification. Therefore, our protocol could resist the replay attack.
If the adversary Φ wants to impersonate the user A to the server S, he has to generate the correct messages (IDA, ZAS), where ZAS = H(1, IDA, IDB, RA, RS1, KAS) and KAS = Ta(RS1 + PWA) = Ta· S1(x) mod P. However, Φ cannot generate the correct KAS without knowing the password of user A, and Φ cannot generate the correct ZAS without knowing the correct KAS. Therefore, it is impossible for Φ to impersonate the user A to the server S. Through a similar method, we could show Φ cannot impersonate the user B to the server S.
If the adversary Φ wants to impersonate the server S to the user A, he has to generate the correct message (ZSA), where ZAS = H(2, IDA, IDB, RA, RB, KSA). However, Φ cannot generate the correct KSA without knowing the password of user A, and Φ cannot generate the correct ZAS without knowing the correct KSA either. Therefore, it is impossible for Φ to impersonate the server S for the user A. Through a similar method, we could show that Φ cannot impersonate the server S to the user B.
The adversary Φ could intercept the messages (RA, RS1, ZAS, ZSA) transmitted between the user A and the server S. Φ guesses a password pA and computes 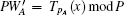
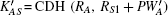
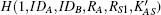

In our protocol, S checks whether ZAS and H(1, IDA, IDB, RA, RS1, KSA) are equal. If it holds, S could deduce that A has the private key pwA, and authenticate the user A simultaneously. From a similar method, S could authenticate the user B.
A checks whether ZSA and H(2, IDA, IDB, RA, RB, KAS) are equal. If it holds, A could deduce that Shas the private key pwA, and authenticate the server S simultaneously. From a similar method, user B could authenticate the server S.
Thus, our protocol achieves the mutual authentication.
Perfect forward security means the compromise that the long-term private keys of one or more entities will not affect the security of other session keys which have been established before. In our protocol, the session key SKAB = H(3, IDA, IDB, RA, RB, KAB) is related to KAB, and KAB is related to nonce a and b, which are chosen by users A and B, respectively. If an adversary wants to compute the previously established session key from RA = Ta(x) and RB = Tb(x), then he will face the CDH problem. Thus, our protocol could provide perfect forward secrecy.
In this section, we analyze the performance of a three-party key agreement protocol based on the extended chaotic map. Smart cards are not available in these protocols. We compare our protocol with Lai et al.’ s protocol and Farash et al.’ s protocol in terms of communication round and computational cost. For the convenience of evaluating the computational cost, some notations are defined as follows:
i) TC: The Chebyshev chaotic map operation,
ii) TE: The symmetric encryption or decryption operation,
iii) TH: The hash function operation.
| Table 2. Comparison with other protocols. |
According to Ref. [20], the time cost of these operations implemented in the environment (CPU: 3.2 GHz, RAM 3.0 G) satisfies the following: TC ≈ 72TE ≈ 161TH, TE ≈ 2.3TH.
To count the number of communication rounds, we adopt two notions, a step and a round which are defined in Ref. [35]. One step is the event that one party sends communicating messages to a single party once. A round is defined as a set of all independent steps that can be processed in parallel.
As can be seen in Table 2, Farash et al.’ s protocol is vulnerable to off-line password guessing attack. Lai et al.’ s protocol made use of the public key to achieve strong security, while our protocol also achieves strong security without using the server’ s public key. The total computational costs are 10TC + 8TH for the proposed protocol, 10TC + 12TH for Farash et al.’ s protocol, and 22TC + TE + 10TH for Lai et al.’ s protocol. As is well known, a symmetric encryption/decryption operation and a hash operation have the same computational cost. Compared with a hash operation, a chaotic map operation is a time-consuming operation. Therefore, the proposed protocol is more efficient than Farash et al.’ s protocol and Lai et al.’ s protocol. Furthermore, the proposed protocol needs only four communication rounds rather than six communication rounds to fulfill the authentication.
Therefore, the proposed protocol not only enjoys efficiency, but also achieves security requirements.
In this paper, we analyze Farash et al.’ s protocol, and propose an improved version with formal proof that preserves the merits of the original scheme. Without any server’ s public key and symmetric cryptosystems, the proposed protocol requires only four communication rounds to fulfill authentication. Security and performance analyses show the proposed protocol not only has better performance, but also achieves strong security. Hence, the new protocol is more efficient and practical.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|