†Corresponding author. E-mail: wangqianxue@gdut.edu.cn
*Project supported by China Postdoctoral Science Foundation (Grant No. 2014M552175), the Scientific Research Foundation for the Returned Overseas Chinese Scholars, Chinese Education Ministry, the National Natural Science Foundation of China (Grant No. 61172023), and the Specialized Research Foundation of Doctoral Subjects of Chinese Education Ministry (Grant No. 20114420110003).
In this paper, the structure of a new chaotic bitwise dynamical system (CBDS) is described. Compared to our previous research work, it uses various random bitwise operations instead of only one. The chaotic behavior of CBDS is mathematically proven according to the Devaney's definition, and its statistical properties are verified both for uniformity and by a comprehensive, reputed and stringent battery of tests called TestU01. Furthermore, a systematic methodology developing the parallel computations is proposed for FPGA platform-based realization of this CBDS. Experiments finally validate the proposed systematic methodology.
Current rapid developments of digital technologies and the Internet have led to tremendous convenience in people’ s work and life. At the same time, new issues appeared such as copyright infringement and information tampering, so that data confidentiality, integrity, and authentication are now difficult to guarantee. Therefore, the need to find new tools to reinforce trust and security through the Internet has become a major concern. Chaotic systems are often proposed to achieve security, due to their properties of sensitivity to initial conditions, topological transitivity, decaying autocorrelation function, and so on.[1, 2] Hence the chaotic system has recently emerged as a new research direction to reinforce information security of data sent through the Internet.[3– 6]
It is obvious that to consider chaos for information security requires a particularly good statistical profile for the associated system used to achieve security.[7, 8] However, until now, almost all studies of chaotic systems applied to information security consider the real domain.[9– 11] As all operations in each iteration manipulate real numbers, any Real Domain Chaotic System (RDCS) designed in a computer or a digital device will inevitably lead to dramatic finite precision effects.[12] Furthermore, continuous-time chaotic systems have to be converted to chaotic sequences, leading to rounding errors.[13] Thus each iteration of the discrete dynamical system will bring a tiny error, due to the sensitivity to initial conditions and the approximations resulting from the real numbers to finite precision binary digits conversion. The chaotic system finally experiences a long-term evolution with cumulative effects of these small errors, which often leads to dynamics degradation such as decayed distribution, low linear complexity, short cycle length, and so on.[5] This degradation directly affects the statistical properties of chaotic systems.[14, 15] The fundamental reason is that chaotic systems are strongly dependent on their initial conditions: small errors at the beginning of iterations will result in large differences between actual and theoretical chaotic orbits. Finally, test results show that most of the RDCSs cannot meet the statistical requirements of TestU01, [16] which is widely considered as the most comprehensive and stringent battery of tests.
To put it in a nutshell, finite precision affects the dynamics of RDCS. Although many experimental methods have been proposed to solve this problem, their performances cannot be accurately controlled. As these finite precision effects are inevitable, new ways to prevent dynamics degradation of chaotic systems must be investigated, and one of them is the Integer Domain Chaotic System (IDCS).
In 2010, a research team at the University of Franche-Comté , France, proposed a new IDCS designated as CI (Chaotic Iterations) system.[17] This CI system receives one or two random stream(s) as input, and it mixes them with chaotic iterations. This mixture uses only bitwise operations, thus achieving the speed requirement. Furthermore, theoretical analyses show that, these CI systems on integer domains satisfy various mathematical definitions of chaos like the Devaney’ s one. Since these systems run on finite sets of integer domains, then the finite precision problem is settled, and the transformation from real numbers to binary sequences is not necessary any more. The CI system is one of the effective solutions for the aforementioned issue that occurs in the RDCS case.
The first collaborative work between French and Chinese teams has consisted in chaotically combining two random inputs in order to construct a first CI system, called PRIM CI in Ref. [18], which has led to better statistical properties for the resultant pseudorandom number generator than each input taken alone. Then MARK CI has been introduced in Ref. [19]: a mark sequence has been applied to avoid wasteful duplication of values, and has resulted in an obvious speed improvement. The LUT (Lookup-Table) CI has then been released and studied in depth in Ref. [20]: this last version of the chaotic combination of two input entropic streams has solved flaws exhibited by the MARK CI version of these IDCSs. The second collaborative work has focused on the design and implementation of IDCS by using only one random source. First chaos generation strategy has finally been realized in Ref. [21], through a sample-hold circuit and a decoder circuit so as to convert the uniform noise signal into a random sequence.
In this paper, a new chaotic bitwise dynamical system (CBDS) is proposed, whose dynamics of chaos are still preserved in digital computers. Its obvious speed improvement makes it a good candidate when developing new approaches in some fields regarding information security like digital watermarking, because it uses multiple random bitwise operations instead of only one like in Ref. [21]. Then, its proof of chaos according to the Devaney’ s definition is presented in this paper. After having introduced the theoretical framework of this study, we will give a comparison based on the uniformity of the sequence and on statistical tests. We will then focus on the Field Programmable Gate Array (FPGA) implementation of this CBDS, with the presentation of both theoretical background and practical details. Some specific components like ring oscillator, [22] D flip– flop, iterate function circuit, DAC (digital to analog converter) have been applied to design the FPGA. The main feature of this kind of CBDS circuit is that it takes advantage of parallel computations in FPGA.
The remainder of this research work is organized as follows. The improved version of CBDS is given in Section 2, while its proof of chaos is provided in Section 3. The uniformity and statistical property of this novel version will be evaluated in Sections 4 and 5. FPGA implementation of CBDS are detailed in the next section. This article ends with a conclusion section in which the contributions are summarized (Section 7).
In this section, we first introduce the basic concept of RDCSs and IDCSs.
Let N ∈ 1, 2, ... be a positive integer, B = {0, 1} denotes the set of Boolean numbers with its usual algebraic structure, while BN is the set of binary vectors of size N.
Definition 1 Let f : ℝ → ℝ be a function, and xn and xn− 1 be two real numbers, which are represented as infinite numbers of bits in their binary decomposition:
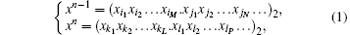
where each element is a Boolean, while xi1xi2… xiM and xj1xj2… xjN are respectively the integral and fractional parts for xn− 1. Similarly, xk1xk2… xkL and xl1xl2… xlP are respectively the integral and fractional parts for xn. The so-called iterative equation in RDCSs is defined by
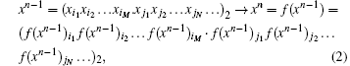
where f (xn− 1)i and f (xn− 1)j are the i-th and j-th components of f (xn− 1) for the integral and fractional parts respectively. In other words, at each iteration, all the binary components of these real numbers are iterated.
Consider now a system with a finite number of N elements (or cells) x = (xN− 1xN− 2… x0), so that each element has a Boolean state: xN− 1, xN− 2, … , x0 ∈ B. Having N Boolean values for these cells leads to the definition of a particular state of the system x = (xN− 1, xN− 2, … , x0) ∈ BN. A one-sided infinite sequence of integers bounded by N − 1 is called a strategy: ∀ n ∈ ℕ , sn ∈ {0, 1, 2, … , N − 1}.
Definition 2 (Ref. [21]) Let f : BN → BN be a function, 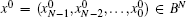
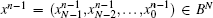
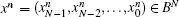
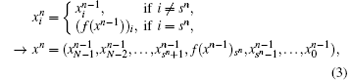
where i = 0, 1, 2, … , N − 1, n = 1, 2, … , and f (xn− 1)sn is the sn-th component of f (xn− 1). In other words, at the n-th iteration, only the sn-th element is iterated.
The major difference between CBDS and the basic IDCSs published in Ref. [21] is that wn is a subset (wn ⊂ {1, 2, … , N}) instead of a single integer (sn ∈ {1, 2, … , N}).
Definition 3 In the so-called CBDS, the iterative equation is defined as follows:
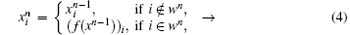
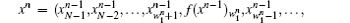
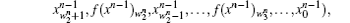
where i = 0, 1, 2, … , N − 1, n = 1, 2, … , and ∀ n, wn is a set, which can be represented by a one-sided infinite sequence of integers bounded by N − 1 as 
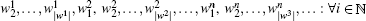
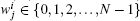
The subset wn can be expressed as an integer pn having N bits: the k-th digit in the binary decomposition of pn is 1 if and only if k belongs to wn (the other digits are set to 0). That is, the size of the set wn is the number of 1’ s in the binary decomposition of pn while the elements in the set wn are the positions of these 1’ s. The state xn of the system, for its part, is similarly represented as an integer yn having N bits. Therefore, the iterative equation is as follows:
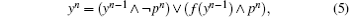
where ∧ is the logical conjunction, ∨ is the disjunction, and ¬ is the negation. This formula means that the k-th component of state yn (a binary digit) is updated by (f (yn− 1))k if and only if the k-th digit in the binary decomposition of pn is 1. Remark that in our previous research works the iterate function f has often been the vectorial negation, [21] given by
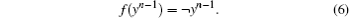
With such a choice, a more specific formula can be obtained
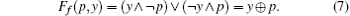
Let E = (p, y) be a couple constituted by a chaotic strategy and a binary digit, consider the phase space:
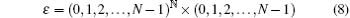
and the map defined on ε with E = (p, y) ∈ ε :
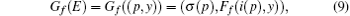
where i(p) = p1 and 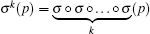
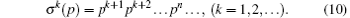
Then the iterative equation proposed in Definition 3 can be rewritten as follows:
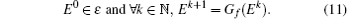
To study the Devaney’ s chaos property, a distance between two points (p, y) and 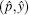
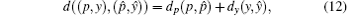
where p = p1p2p3 … pn … and 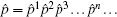
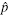
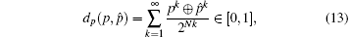
where 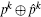
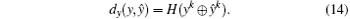
Remark that where H(X) is the hamming weight of X and d is defined as the sum of two other distances. Before investigating the chaotic properties of CBDS, the following lemma is first introduced.
Lemma 1 Let the p = p1p2p3 … pn … and the 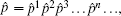
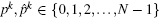
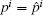
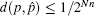
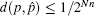
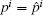
Proof If 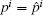
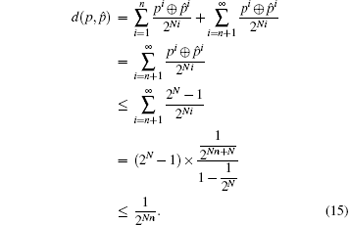
Conversely, and due to the definition of the proposed distance: for any m ≤ n, if 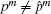
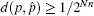
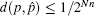
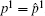
In this section, the chaotic behavior of CBDS is proven according to the Devaney’ s definition recalled below.
Definition 4 (Devaney’ s definition of chaos[24]) Let 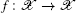
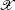
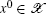
D4-a its periodic points are dense in 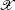
D4-b it is transitive: for any nonempty open sets UA and UB in (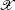

D4-c it has sensitive dependence on initial conditions.
The meaning of these properties are detailed thereafter.
Theorem 1 (Banks[25]) If a dynamical system is transitive and has dense periodic points, then it has sensitive dependence on initial conditions.
Thus, to prove that we are in the framework of Devaney’ s topological chaos, we have to check the regularity and transitivity conditions.
Theorem 2 The periodic points of Gf are dense in ε .
Proof Let 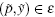
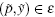
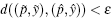
P1 The general form of 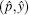
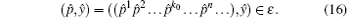
As ε can be strictly lesser than 1, we must choose ỹ = ŷ , because if ỹ ≠ ŷ , then dy(ỹ , ŷ ) ⩾ 1, 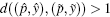
P2 Let us define
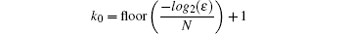
according to the previous Lemma 1, and let us consider that the first k0 elements of 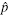
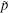
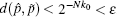
P3 If after k0-th iteration, we have
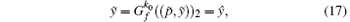
then a cycle point 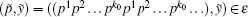
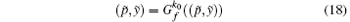
making

true.
P4 Suppose that, after the k0-th iteration, we have
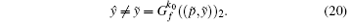
To obtain that, after another iteration, the following condition is met
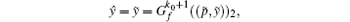
we must set: 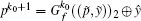
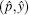
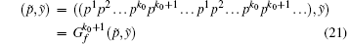
making
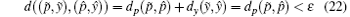
true.
In summary, the periodic points of Gf are dense in ε .
Theorem 3Gf is a transitive map on ε .
Proof Consider two nonempty open sets UA and UB, and (pA, yA) ∈ UA, (pB, yB) ∈ UB. UA and UB are open, and we take place in a metric space, so there exist real numbers rA > 0 and rB > 0 such that the open ball ℬ A of center (pA, yA) and radius rA is inside UA (resp. the open ball ℬ B of center (pB, yB) and radius rB is into UB). Without loss of generality, we can suppose that rA < 1.
P-a We introduce the following notations:
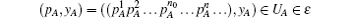
and
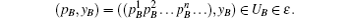
P-b Let 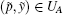
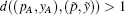
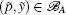
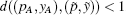
P-c If we demand that the k0 first elements of 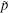
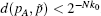
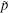
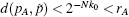
P-d If after k0 iterations, the following condition is satisfied
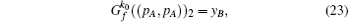
then n0 = k0 and 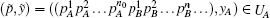
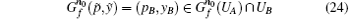
making
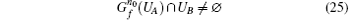
true.
P-e If after the k0-th iteration, 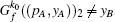
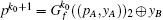
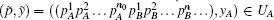
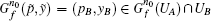
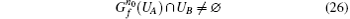
true.
In summary, (Gf, ε ) is transitive.
Because of dense periodic points and transitivity, and according to Definition 1 and Theorem 1, we can conclude that CBDS is chaotic in the sense of Devaney.
Definition 5 (Uniform probability index) Let α be a random variable with a Bernoulli distribution. So
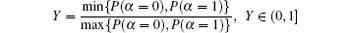
is called the uniform probability index of α .
The uniform probability index Y characterizes the uniformity of the binary sequence. In particular, if Y = 1, then α is distributed evenly. The larger Y, the more uniform for α .
Theorem 4 Let α be a sequence of random variables having a Bernoulli distribution and β n being a sequence of random variables defined by: β 0 is a random variable with a Bernoulli distribution, and ∀ n, β n+ 1 = β n⊕ α n. Then the uniformity of β is better than the one of α , in the sense that ∀ n, Yβ n ≥ Yα n.
Proof Let P(β 0 = 0) = b and P(α 0 = 0) = a.
P-i Let us prove that the statement holds when n = 1
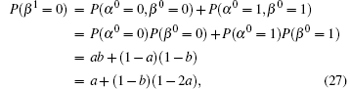
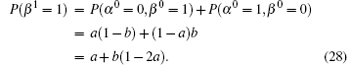
When a ≤ 1/2 then 1 − a ≥ 1/2, so we get
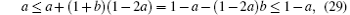
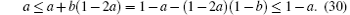
Conversely, when a ≥ 1/2 then 1 − a ≤ 1/2, and the above two inequalities still hold, while the equality holds if and only if a = 1/2. Taking these two cases into account, we have:
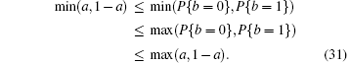
These inequalities combined with Definition 5 leads to 1 ≥ Yβ n ≥ Yα n, and the base case is obtained.
P-ii Suppose that the statement holds for a given n. Redefine a and b such that P(β n = 0) = b while P(α n = 0) = a. Then
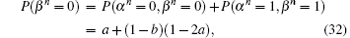
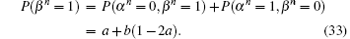
The same canvas of proof as for the base case leads to the fact that the same statement holds for n + 1, which concludes the proof.
Corollary 1 Let pn be a sequence of random independent variables of integers having N bits, y0 be an integer random variable, and (yn) a sequence of random variables defined by yn+ 1 = yn⊕ pn. Then the binary sequence represented by yn is more uniform than the one represented by pn.
This corollary is an obvious consequence of the aforementioned theorem.
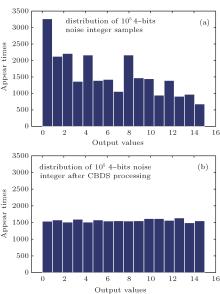
In order to evaluate this conclusion, density histograms have been computed. In these experiments, the length of pn and yn is N = 4 bits, while a large number of sampled values are simulated (105 samples). Figure 1(a) shows that, as expected, the histogram is not uniformly distributed in all areas for pn when P(pn = 0) = 0.6 and P(pn = 1) = 0.4. It can however be observed that a uniform histogram is obtained for yn, and we have P(y = 0) ≈ P(y = 1) ≈ 0.5 for CBDS, see Fig. 1(b). This first evaluation of the uniformity in CBDS is systematically verified using numerous tests presented in the next section.
There are many approaches to analyze the safety performance of chaotic systems used in information security, depending on which aspect sounds important. These approaches encompass speed, cryptographical security, or statistical profile evaluation. This paper is a prerequisite for numerous applications, it is quite quick and simple to evaluate through reputed batteries of tests. Furthermore it does not need to consider the internal structure of the chaotic system, which explains why using such batteries becomes an internationally accepted analytical tool for PRNGs.
Various statistical tests are available in the literature that test a given sequence for some level of computational indistinguishability with a truly random stream. Major test suites for random sequences are TestU01, the NIST suite, [26] and the DieHARD one.[27] DieHARD suite, which implements many classical tests, has revealed over time some drawbacks and limitations. The National Institute of Standards and Technologies (NIST) in the United States, for its part, has implemented a suite (16 tests) for testing random sequences. It is geared mainly for the test and certification of random sequences used in cryptographic applications. Finally, TestU01 is extremely diverse in implementing classical tests, cryptographic tests, new tests proposed in the literature, and original ones. In fact, it encompasses most of the other test suites. The proposed CBDS has been evaluated using TestU01 for its statistical randomness.
Table 1 lists seven batteries of tests in the TestU01 package. “ Standard” parameter in this table refers to the built-in parameters of the battery. TestU01 suite implements 518 tests and reports p-values. If a p-value is within [0.001, 0.999], the associated test is a success. A p-value lying outside this boundary means that its test has failed. The intention of CBDS is to enhance the effects of chaotic and random behaviors, to improve the statistical properties relative to pn. This CBDS may utilize any reasonable random sequence as pn. For demonstration purposes, ISAAC are adopted here. The yn with this input can pass all of the performed tests.
| Table 1. TestU01 statistical test. |
The design principle of CBDS is described and verified in this section.
The CBDS construction starts with the noise source design, which has been developed using ring oscillators. A ring oscillator is a device composed of an odd number of NOT gates as shown in Fig. 2, whose output oscillates between two voltage levels, representing true and false. As it is depicted, the output of the last inverter is fed back into the first one. Because a single inverter computes the logical NOT of its input, it can be deduced that the last output of a chain of an odd number of inverters is the logical NOT of the first input. This final output is asserted a finite amount of time after the first input is asserted, and thus, the feedback of this last output to the first input causes oscillation.
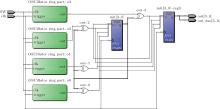
A multiple ring-based design was developed with several ring oscillators with different ring lengths. Here we use three rings, each with the long length gates. The three rings (as shown in Fig. 2) are XORed together to generate the output signal, as described in Fig. 3, where ring3:r31, ring3:r32, and ring3:r33 are the three long ring oscillators. The ring lengths for several ring oscillators were chosen in the range of relatively prime.[28]
The ring oscillator output once XORed is sampled using the D flip– flop as shown in Fig. 3, the ‘ trigger’ input has to be carried out from lower or similar frequencies of the ‘ clk’ , this can cause more metastability effects in the D flip– flop, which can cause more metastability effects in the D flip– flop, which reduces the mutual coupling effects. The output has later to be subjected to post processing, that is, to chaotic iterations.
Each multiple ring oscillator outputs one component of state pn (a binary digit). For our experiments, we have decided that pn will be constituted by four binary digits, which means that N = 4. The iterative equation is yn = yn− 1 ⊕ pn as shown in Fig. 4. Two D flip– flops are used to store state information: init[3...0] is for y0 while out[3...0] reg0 stores yn− 1.
The experimental observations of CBDS are finally shown in Fig. 5. Then a 108-bits long CBDS sequence is generated and passes the NIST statistical test suite.
In order to solve degradation of chaotic dynamical properties by finite precision effects in traditional RDCS, the structure of a new CBDS, which uses random bitwise operations instead of only one, has been described. Its proof of chaos according to the Devaney’ s definition has been provided too. A comparison based on the uniformity of the outputs and on statistical tests has verified the good statistical profile of the generator. Finally, the performances of the corresponding FPGA-based implementation have been evaluated, confirming the feasibility and applicability of CBDS. These considerations enable us to claim that this CBDS offers a sufficient speed and level of security for a whole range of applications where secure generators are required as cryptography and data hiding.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|