Transmission lines, such as power lines, control lines, and data lines, are the most important coupling path through which an external electromagnetic pulse (EMP) interacts with electronic systems.^{[1, 2]} Transmission lines have been extensively investigated.^{[1– 15]} Most of them focused on transmission lines with exact positions. However, many transmission lines are hard to fix exactly and have randomness in real life. The induced interferences generated by external fields on these random transmission lines are random, too. Consequently, the analysis of fields coupling to a random transmission line should be studied to help the evaluation of the effects on electronic systems induced by external fields.

The Monte Carlo (MC) method combined with transmission line theory or numerical simulation has been used to obtain the statistical results of electromagnetic fields coupling with transmission lines, ^{[13– 16]} where the MC method was employed to model random transmission lines and then transmission line theory or numerical simulation was used to calculate the interferences on each sample. However, this method is not efficient. Because nonuniform transmission lines can be approximated as a series of cascaded segments of a uniform transmission line, the study of a uniform transmission line with random movement is the basis and important. A plane wave coupled multiconductor transmission line with random translation over ground has been analyzed in Ref. [17] where an efficient method was proposed for evaluating the average induced voltages and the probability distribution of the voltage variation. However, multiconductor transmission lines with random rotation have not been studied yet.

In this paper, a plane wave coupled transmission line with random rotation over an infinite and perfectly conducting ground is studied. Based on the analysis of the influence factors of the random voltages generated by the plane wave, a simple and efficient calculation method is proposed for the average induced voltages. The results are in good agreement with those via the MC method but the proposed method is more efficient. The study also implies that the effect of random rotation is important and should be considered compared with that of random translation.

For a uniform transmission line rotating randomly over an infinite and perfectly conducting ground under the excitation of an incident electromagnetic field as shown in Fig. 1, the transmission line equation can be written from Agrawal’ s model as^{[1, 3]}

Here α is the rotation angle of the line shown in Fig. 1. V^sca and I are the scattered line voltage vector and the line current vector, respectively. L and C are the per-unit-length (p.u.l.) inductance and capacitance matrices of the line. V_F2 is a distributed voltage source vector which denotes the effect of the external fields along the line. The boundary condition is given by

where Z_S and Z_L are the impedance matrices at the near and far ends, V^ex is the lumped voltage source at the line end due to the excitation field.^[3] The diagram for the Agrawal model of a transmission line is shown in Fig. 2.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. A multiconductor transmission line over the ground, excited by an incident field.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Diagram for the Agrawal model of field coupling with transmission lines.

When the transmission line rotates randomly over the ground, the matrices L, C, and the voltage source vector V_F2 change randomly, which leads to the random voltage and current vectors.

The voltage vector V(α , z) is continuous and differentiable. Thus according to Ref. [17], when the rotation angle α is a small quantity, then the averages of the induced voltages and currents can be approximated by

where the symbol 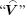denotes the value at the average rotation angle ᾱ . and conform to the equation and the boundary condition as

and

As a result, the voltage variation and current variation can be written as

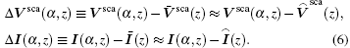
Substituting and into Eq. (1), subtracting the result from Eq. (1), and ignoring the second-order small quantities, the voltage variation and current variation satisfy the equation and the boundary condition as

and

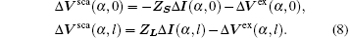
When the transmission line rotates on the ground, with a plane wave coupled, there are two factors that affect the induced voltages. One is the changes of the line parameters, such as p.u.l. inductance and capacitance matrices, and the other is the change of the source term V_F2. As a result, the voltage and current variations Δ V^sca and Δ I are composed of two components, Δ I_p and , Δ I_ex, which denote the voltage and current variations due to the changes of line parameters and source term, respectively. According to Eqs. (7) and (8), , Δ I_p and , Δ I_ex satisfy the following equations:

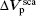
and

respectively. The corresponding boundary conditions for, Δ I_p and 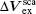, Δ I_ex are described by

and

As described above, there are two factors affecting the induced voltage and current. The effects of these two factors are analyzed below.

Comparing Eq. (9) with the transmission line equation for the inner transmission line system of shielded cable in Ref. [18], it can be concluded that equation (9) is similar to the transmission line equation of the inner system of shielded cable. Thus and Δ I_p have the same relationship between and as that between the voltage V_in and current I_in of the inner system and the voltage V_out and current I_out of the outer system of shielded cable. Δ L and Δ C are equivalent to the transfer inductance L_t and capacitance C_t of shielded cable. The results in Ref. [18] show that the voltage V_in and current I_in can be about four and three orders of magnitude smaller than the voltage V_out and current I_out in the low and high frequency ranges, respectively. The transfer inductance L_t and capacitance C_t are about 1 nH and 0.1 pF, respectively. The inductance variation Δ L has the same order of magnitude as L_t, and the capacitance variation Δ C is one order of magnitude smaller than C_t when the rotation quantity Δ α is 0.0873 rad, which will be illustrated in the numerical validation in Section 5. As a result, the voltage variation due to the parameter change being about four and three orders of magnitude smaller than in the low frequency range (below 1 MHz) and in the high frequency range (1 MHz to 1GHz), respectively. Thus the values of are smaller than 0.001 and 0.01 in the low and high frequency ranges, respectively.

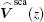
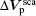
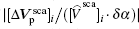
Comparing Eq. (10) with Eq. (4), equation (10) has the same form as Eq. (4), except the variables and the source term. When the incident wave is a plane wave, the source terms for and can be derived from Ref. [2] and are given by

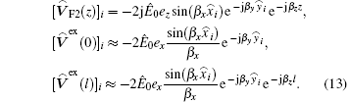
When the rotation quantity δ α is a small quantity, the source terms for Δ V_ex and Δ I_ex can be written as

where

It can be derived from Eq. (15) that

is much larger than . This means that the source term has a larger influence than the parameters.

To indicate the influence of the random rotation, we define the sensitivity and relative sensitivity of the induced voltage to the rotation angle as and , respectively. Then the voltage variation due to random rotation can be expressed as Δ V ≈ S_α · δ α or . The components of the S_α and S_rα are denoted by S_{α p}, S_{rα p} and S_{α ex}, S_{rα ex}, which denote the influences of the line parameter and the source term, respectively. As discussed above, S_{α ex} and S_{rα ex} are much larger than S_{α p} and S_{rα p}. With Eqs. (7), (9), (10), and the definitions of the sensitivity and relative sensitivity, the sensitivity, the relative sensitivity, and their components can be calculated.

When the rotation quantity δ α is a small quantity, the average voltage can be computed through Eqs. (4) and (5) by using the Baum– Liu– Tesche (BLT) equation ^[1] or the SPICE model.^[2] However, in reality it is very common that the rotation quantity may be large. The wire bundle rotating in the interval [− π , π ] uniformly is the most common case. Because the effect of the parameter change is much weaker than that of the excitation field change and the voltage variation is mainly due to the change of the excitation field no matter what the angle α is, the effect of the parameter change can be ignored and the average voltage and current, when the wire rotates uniformly in the interval [− π , π ], can be approximately solved by

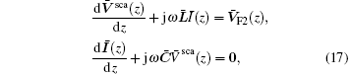
and

Here, and C̄ are the inductance and capacitance matrix computed by using the average parameter, that is, the average position of the wire, and are given by

where μ and ε are the permeability and permittivity of the medium around the wire, h is the height of the line, as shown in Fig. 1, a_i is the radius of the i-th wire, and d_ij is the distance between the i-th wire and the j-th wire. V̄ _F2(z), V̄ ^ex(0), and V̄ ^ex(l) are the average source terms when the angle α distributes uniformly in the interval [− π , π ] and they can be approximated by

when β r_i ≪ 1.

Figure 1 shows a four-wire transmission line with a length of 2 m over a perfectly and infinitely conducting ground. The distance r₀ between the wire and the center o′ is 2 mm. The height h of the center o′ over the ground is 15 mm. The radii of the wires are all 0.68 mm. The initial angles between the x axis and the wire 1, wire 2, wire 3, and wire 4 are π /4, 3π /4, 5π /4, and 7π /4, respectively. The near-end impedances Z_S1, Z_S2, Z_S3, and Z_S4 of the wires are 50 Ω , 60 Ω , 80 Ω , and 100 Ω , respectively. Their far-end impedances Z_L1, Z_L2, Z_L3, and Z_L4 have the same values as Z_S1, Z_S2, Z_S3, and Z_S4, respectively. The transmission line is 2-m long. The incident field is a sine wave with unit magnitude and a frequency of 100 MHz. The incident and polarization angles are θ _p = π /4, ϕ _p = − π /3, and θ _E = π /2, where the definition of the incident and polarization angles can be found in Fig. 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Definition of the incident and polarization angles.

To illustrate the weight of the effects of changes in the parameters and the source term on voltage variation, the variations of the inductance and capacitance are given first and then the values of S_{α p} and S_{α ex} are given.

When the rotation quantity δ α is 0.0873 rad (or 5° ), the L and C matrices at the new position can be computed by using the line parameter. Then Δ L and Δ C can be obtained by subtracting the old values of the L and C matrices from the new ones, and they are given by

Δ L has the same order of magnitude as the transfer inductance L_t of shielded cable, and Δ C is one order of magnitude smaller than the transfer capacitance C_t of shielded cable. As discussed above, the values of are smaller than 0.001 and 0.01 in the low frequency range (below 1 MHz) and the high frequency range (1 MHz to 1 GHz), respectively. According to Eq. (16), equals 0.09 approximately. Thus S_{α ex} is much larger than S_{α p}. From Eqs. (9)– (12) and the definition of the sensitivity, S_α , S_{α p}, and S_{α ex} can be calculated. The voltage sensitivities and their components for the loads Z_S1, Z_S2, Z_L1, and Z_L2 at the average height are given in Table 1. It can be seen from the results that S_{α ex} is much larger than S_{α p} and S_{α ex} has the opposite polarity to S_{α p}, which implies that the effects of the source term and the parameter are opposite.

Table 1.

Table 1.

Table 1. Sensitivities obtained by the proposed method. Sα p/(mV/rad) Sα ex/(mV/rad) Sα /(mV/rad) ZS1 – 0.031– 0.064i 0.236+ 0.358i 0.205+ 0.295i ZS2 – 0.028-0.096i 0.206+ 0.429i 0.177+ 0.334i ZS3 0.025+ 0.135i – 0.320– 0.623i – 0.295– 0.488i ZS4 0.016+ 0.121i – 0.251– 0.694i – 0.235– 0.573i ZL1 – 0.032– 0.080i 0.243+ 0.456i 0.210+ 0.376i ZL2 – 0.032– 0.121i 0.215+ 0.546i 0.183+ 0.425i ZL3 0.030+ 0.168i – 0.332– 0.783i – 0.301– 0.614i ZL4 0.022+ 0.151i – 0.277– 0.731i – 0.256– 0.731i

Table 1. Sensitivities obtained by the proposed method.

To validate that the effect of the source term plays a main role, the sensitivity, the relative sensitivity, and their components versus the frequency, the magnitude of incident wave, and the rotation angle are also studied.

Figure 4 shows the sensitivity, the relative sensitivity, and their components versus the magnitude of the incident field. The results imply that the sensitivity is linearly and directly proportional to the magnitude of the incident field but the relative sensitivity does not depend on the magnitude of the incident field and the dominance of S_{α ex} does not change with the magnitude of the incident wave. It can also be concluded that larger voltage variation will be observed if the external field is larger but the influence does not change with external field because the induced voltage also increases.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Variations of (a) sensitivity and (b) relative sensitivity at the load ZS1 with the magnitude of the incident field.

Figure 5 shows the changes of the sensitivity and the relative sensitivity at the load Z_S1 with rotation angle. The results show that the sensitivity, the relative sensitivity, and their components change with the rotation angle periodically and they have the same trends. The results also show that the dominance of S_{α ex} does not change with the rotation angle.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Variations of (a) sensitivity and (b) relative sensitivity at the load ZS1 with rotation angle.

Figures 6(a) and 6(b) show the variations of the sensitivity and the relative sensitivity at the load Z_S1 with frequency. Results show that S_{α p} and S_{α rp} are far smaller than S_{α ex} and S_{α rex} in the low frequency range, respectively, but the distinction between them becomes small in the high frequency range. The results also show that S_{α ex} and S_{α rex} dominate in the frequency range under study.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Variations of (a) sensitivity and (b) relative sensitivity at the load ZS1 with frequency.

As illustrated above, the effects of source term dominate in the voltage variation.

When the rotation angles are distributed uniformly in the interval [− π , π ], the average voltages induced by external fields computed via Eqs. (17)– (20) are given in Table 2, which are in good agreement with those obtained by the MC method. In the MC method, the number of samples is 8000 and the BLT equation is adopted to calculate the voltage of each sample. Thus the time taken by the proposed method is about 1/8000 times that taken by the MC method. The average voltages obtained by the proposed method and the MC method, when the distance r₀ between the wire and the center o′ is 10 mm, are given in Table 3, where the results of the two methods agree well with each other.

Table 2.

Table 2.

Table 2. Average voltages obtained by the proposed method and the MC method when r0 is 2 mm. Proposed method Monte Carlo VZS1/mV – 1.43– 0.40i – 1.43– 0.39i VZS2/mV – 1.47– 0.52i – 1.47– 0.51i VZS3/mV – 1.59– 0.85i – 1.59– 0.84i VZS4/mV – 1.53– 1.00i – 1.54– 1.00i VZL1/mV – 1.37– 0.58i – 1.37– 0.58i VZL2/mV – 1.41– 0.74i – 1.41– 0.72i VZL3/mV – 1.54– 1.15i – 1.54– 1.13i VZL4/mV – 1.50– 1.34i – 1.51– 1.35i

Table 2. Average voltages obtained by the proposed method and the MC method when r0 is 2 mm.

Table 3.

Table 3.

Table 3. Average voltages obtained by the proposed method and the MC method when r0 is 10 mm. Proposed method Monte Carlo VZS1/mV – 2.04– 0.86i – 2.02– 0.81i VZS2/mV – 2.23– 1.14i – 2.20– 1.08i VZS3/mV – 2.55– 1.74i – 2.54– 1.65i VZS4/mV – 2.58– 2.23i – 2.60– 2.16i VZL1/mV – 1.97– 1.17i – 1.94– 1.12i VZL2/mV – 2.15– 1.52i – 2.11– 1.45i VZL3/mV – 2.47– 2.24i – 2.46– 2.14i VZL4/mV – 2.52– 2.86i – 2.54– 2.76i

Table 3. Average voltages obtained by the proposed method and the MC method when r0 is 10 mm.

Now, we compare the effects of the random translation and random rotation for this line structure. According to Ref. [17], the relative sensitivity S_hr, when this line translates over the ground, is about 66.6 m^{− 1} (≈ 1/h) and figure 5(b) shows the maximum of S_{α r} is about 0.5 rad^{− 1}. The value of S_hr is much larger then that of S_{α r}. However, it is impossible for a line to translate randomly with large quantity, and the translation quantity is usually small, say, 10 mm. But the line may rotate in its cross section with large angles and the polarity of the voltage may change with the rotation angle as shown in Fig. 5. As a result, the effect of random rotation has a larger effect on the voltage of the line than that of random translation in reality and the influence of the random rotation should be considered.

In this study, we analyze a plane wave coupled transmission line rotating randomly over an infinite and perfectly conducting ground and propose an efficient method to calculate the average voltage. The voltage variations induced by the changes of the line parameters and excitation field are investigated. The voltage variation is mainly due to the change of the source term. The results show that the sensitivity of the voltage to the rotation increases linearly with the magnitude of the incident wave and changes periodically with the rotation angle. The results also show that the random rotation has a larger influence on the induced voltages in the high frequency range than in the low frequency range. The average voltages obtained by the proposed method are in good agreement with those obtained by the MC method and the proposed method is much more efficient. The results also show that the effect of random rotation is more important than that of random translation.