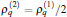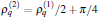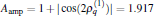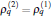†Corresponding author. E-mail: stsbcg@mail.sysu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 10874249).
The evolution of two-component cold atoms on a ring with spin–orbit coupling has been studied analytically for the case with N noninteracting particles. Then, the effect of interaction is evaluated numerically via a two-body system. Two cases are considered: (i) Starting from a ground state the evolution is induced by a sudden change of the laser field, and (ii) the evolution starting from a superposition state. Oscillating persistent spin-currents have been found. A set of formulae have been derived to describe the period and amplitude of the oscillation. Based on these formulae the oscillation can be well controlled via adjusting the parameters of the laser beams. In particular, it is predicted that movable stripes might emerge on the ring.
It is well known that the study of the motion of charged particles under a magnetic field is an essential topic in both macroscopic and microscopic physics. In particular, a number of distinguished quantum mechanical phenomena, such as the Aharonov– Bohm (AB) oscillation and the fractional quantum Hall effect (FQHE), are caused by the magnetic gauge field.[1– 3] After the experimental realization of the condensation of neutral atoms with nonzero spin, [4] a great interest is to create a light-induced gauge vector field to achieve the spin– orbit coupling (SOC) so that various magnetic– electronic phenomena of charged particles occurring in condense matters can be copied into the world of condensates of neutral atoms.[5– 9] Since 2005 there have been proposals by the theorists for producing the light-induced gauge vector field for the condensates with multi-component neutral cold atoms.[10– 15] The first experimental realization of the SOC in condensates was implemented in 2009 by dressing the cold atoms with two counter propagating polarized laser beams.[16, 17] This technique opened a new perspective in the field of BEC, and more and more experimental[18– 21] and theoretical[22– 24] results have been reported. It was found that the total magnetization (or spin-polarizability, which measures the difference of the densities of the spin-components) varies with time. It implies the existence of spin-currents.[12, 16, 22] Besides, the collective-mode dynamics has been studied, the spatial motions along different directions could be correlated (say, a dipole mode might induce a breathing mode in its perpendicular plane).[24] The instability caused by the collective mode has also been studied.[23]
On the other hand it is now possible to trap a condensate in ring geometry. Long-lived rotational superflows have been induced in this kind of system.[20, 25– 33] The creation of the spin-currents of two-component condensates on a ring, due to the introduction of the laser beams, has been experimentally realized.[20] It was found that the stability depends strongly on the initial ratio of the two components.[20] However, the oscillation of the spin-currents on the ring has not yet been observed.
Obviously, the study of the cold spin-currents (i.e., the current of each spin-component) caused by the SOC is just beginning. It is expected that the oscillation of the spin-currents might also emerge in the ring geometry (because a circular motion is equivalent to a linear motion with a periodic boundary condition). To confirm this suggestion, a one-dimensional model of the two-component condensates on a ring under SOC is adopted in this paper. The aim is to clarify from the theoretical aspect how the details of oscillation (the period and amplitude) depend on the parameters of the laser beams. We believe that the interaction might not be crucial. Therefore, the interaction is ignored at first so as to emphasize the decisive role of the laser beams. Then, the effect of the interaction is evaluated via a two-body system.
Let the quasi-spin ŝ be introduced to describe the two components of an atom as usual. The atomic state with sz = 1/2 (− 1/2) is named the up- (down-)state. When two counter-propagating and polarized laser beams are applied, due to the SOC, the two components of atoms might move towards opposite directions along the beams and can transform to each other via a spin-flip. When the interaction is ignored, the Hamiltonian is just H = ∑ iĥ i, where ĥ i is for the i-th particle. Disregarding the subscript i,
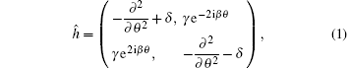
where θ is the azimuthal angle along the ring.[9] The unit of energy is hereafter Eunit ≡ ħ 2/(2mR2), where m is the mass of an atom, R is the radius of the ring. β ≡ k0R, where 2k0 is the momentum transfer caused by the two lasers. γ ≡ Ω /2Eunit, where Ω /2 is the strength of Raman coupling causing the spin-flips accompanied by the momentum transfer. Let ε split be the Zeeman energy difference between the two spin-states, and ω δ is the frequency difference between the two laser beams. We define the Raman detuning δ ≡ (ε split − ħ ω δ )/(2Eunit). In addition to γ , δ is an important quantity because it can be tuned so that the related process could be energy-adapted (see below). Note that, due to the ring geometry, 2β must be an integer. It implies that the transfer of momentum will be suppressed unless the transfer is close to a specific set of values depending on R. Thus, an additional constraint is required under the ring geometry.
To illustrate the connection with conventional SO coupling, we define a U-transformation so that the up-state (down-state) is multiplied by a factor eiβ θ (e− iβ θ ). Then, by introducing the Pauli matrices σ z and σ x, Uĥ U− 1 can be written in a more familiar form as[9, 12, 16, 34, 35]
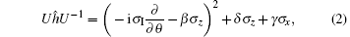
where σ I is just a unit matrix with rank 2. ĥ has two groups of eigenstates, they can be written as[16, 34, 35]

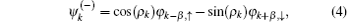
where
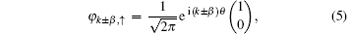

k is an integer (half-integer) when β is an integer (half-integer),
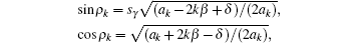
sγ is the sign of γ , 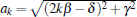
(i) Each of them contains both the up and down components, they are propagating with angular momenta k − β and k + β , respectively. Where 2β is proportional to the momentum transfer caused by the counter-propagating laser beams.
(ii) In each 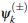
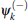
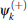
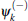
The eigenenergies of 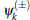
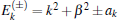
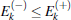
The time-dependent solution ψ (θ , t) of the single-particle Schrö dinger equation starting from an initial state ψ init can be formally written as

where τ ≡ tEunit/ħ (for 87Rb and R = 12 μ m as given in Ref. [20], t = 0.398 τ s), λ = ± , k runs over the (half-) integers when β is the (half-) integer.
In the experiment reported in Ref. [21] a strong oscillation of the magnetization induced by a sudden change of the laser field was reported. It is assumed that a set of parameters β , γ 1, and δ 1 (the first set) are given initially, and the initial state is just the ground state (g.s.) of ĥ as 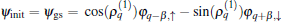
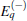
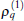
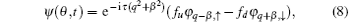
where

and
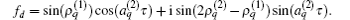
Where 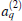
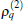
Let the time-dependent densities of the up- and down-components be defined from the identity ψ + (θ , t)ψ (θ , t) ≡ n↑ (θ , τ )+ n↓ (θ , τ ). Then, we have
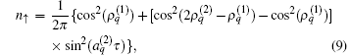
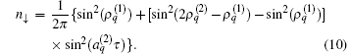
The magnetization (or spin-polarization) is defined as Pz = (n↑ − n↓ )/(n↑ + n↓ ). We have
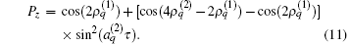
This formula gives a clear picture of a harmonic θ -independent oscillation with a period 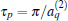
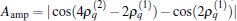
Based on the second set of parameters let us define the energy difference of the two components as
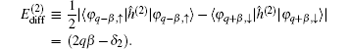
Then, the frequency of oscillation 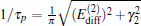
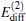
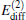
On the other hand, the amplitude Aamp depends on both sets of parameters explicitly. When the first set of parameter has been given so that 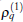
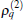
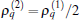
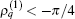
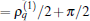
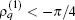
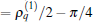
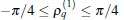


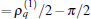
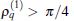

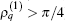
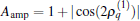
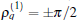
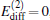
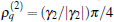
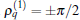
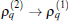
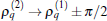
In addition to the densities, one can further define the current based on the equation of continuity as
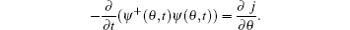
From this definition we found that the current j = j↑ + j↓ in which j↑ ≡ junitn↑ (q − β ) is the current of the up-component and is named up-current, while j↓ ≡ junitn↓ (q + β ) is the down-current, where the unit is junit = ħ /(mR2).[23] The currents are also oscillating with the same period 
The above formulae arise from a single-particle Hamiltonian. For N-particle systems, when all the particles fall into the same state ψ gs initially and the interaction is ignored, it is straightforward to prove that the above formulae hold also.
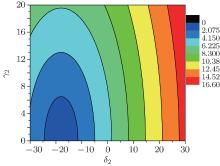
To give numerical results, the radius is given at R = 12 μ m in this paper. A contour diagram for the frequency 1/τ p versus γ 2 and δ 2 is shown in Fig. 1. Where the minimum is located at γ 2 = 0 and 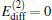
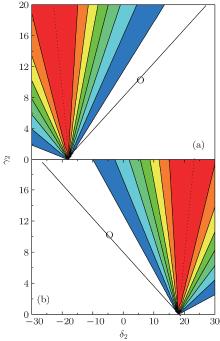
Two contour diagrams for Aamp versus γ 2 and δ 2 with γ 1 and δ 1 being fixed are shown in Fig. 2, where all the contours appear as straight lines. This arises from the fact that 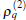
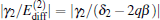
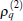
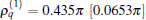
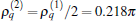
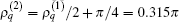
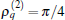
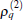
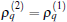
i) The frequency does not depend on the first set of parameters, except q. A larger | γ 2| leads always to a higher frequency which can be further tuned by varying δ 2 around 2qβ . When δ 2 = 2qβ , the frequency arrives at its conditional minimum | γ 2| /π .
ii) Aamp depends on the ratios γ 1/δ 1 and γ 2/δ 2. When γ 2 and δ 2 are given along the solid line (the slope of this line depends on γ 1/δ 1), the sudden change of γ 1 → γ 2 and δ 1 → δ 2 cannot cause an evolution (i.e., Aamp = 0). When γ 2 and δ 2 are given along the dotted line (also depends on γ 1/δ 1), the amplitude will remain unchanged and is conditionally maximized, namely, 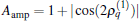
iii) Due to the fact that the contours are straight lines, when γ 2 is small (≠ 0) there is a narrow domain of δ 2 surrounding 2qβ in which Aamp is highly sensitive to δ 2 and appears as a sharp peak. At the peak the amplitude is large while the associated frequency is low.
Recently, the initial state was prepared in a superposition state in an experiment of cold atoms with the ring geometry.[20] In this experiment an additional radio frequency field was used for preparing the initial state
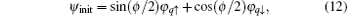
where ϕ determines the initial ratio of the two components and is tunable (0 ≤ ϕ ≤ π ). q is a tunable integer and marks the initial angular momentum of the particle. In this case we have the set of parameters ϕ , q, β , γ , and δ . The corresponding time-dependent solution is
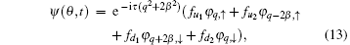
where
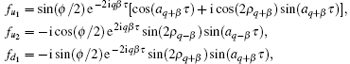
and
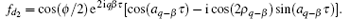
Accordingly, we can obtain the up- and down-densities n↑ (θ , τ ) and n↑ (θ , τ ) given in Appendix A. From them the magnetization Pz can be obtained. It is apparent that, when ϕ = π or 0 (i.e., ψ init is a pure up-state or down-state) the magnetization has a very simple form as
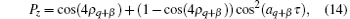
if ϕ = π , or

if ϕ = 0.
These formulae also give a clear picture of harmonic oscillation, but the periods are different for the two cases of ϕ .
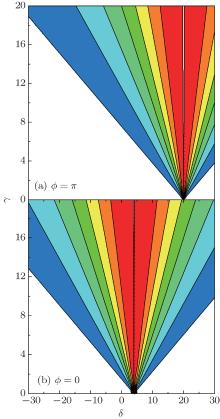
When ϕ = π , τ p = π /aq+ β . If δ is tuned so that δ = 2(q + β )β ≡ δ 0, the frequency will be minimized, namely, 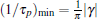
When ϕ = 0, the discussion in the preceding paragraph holds also, except that q + β should be changed to q − β , and δ 0 should be replaced by 2(q − β )β . An example of Aamp is shown in Fig. 3. Figure 3 is of a similar form to Fig. 2 (all the contours are straight lines that converge to a point with γ = 0) except that the dotted line in Fig. 3 is exactly vertical.
When ϕ is neither π nor 0, the oscillation is no longer harmonic. In particular, both the up- and down-densities depend on θ (refer to Appendix A). It implies that the densities are not uniform on the ring as before. Consequently, stripes emerge along the ring, and the stripes move with time. An example of the evolution of Pz is shown in Fig. 4, where the relation δ = 2(q + β )β holds. Accordingly, the curve with ϕ = π has the maximized Aamp = 2 and a minimized frequency. Whereas the curve with ϕ = 0 has a smaller Aamp and a larger frequency. For ϕ = π /2, the anharmonic oscillation is clearly shown.
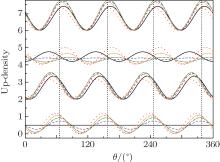
An example of the up-density versus θ with ϕ = π /2 is shown in Fig. 5, where the stripes emerge along the ring. Note that two waves φ q, ↑ and φ q− 2β , ↑ are contained in the up-component, and φ q, ↓ and φ q+ 2β , ↓ in the down-component. The stripes arise from the interference of these waves. Note that one of these waves contains an additional factor e∓ i2β θ . Accordingly, the stripes appear periodically with θ as shown in Fig. 5 and the number of peaks (valleys) in the domain (0, 2π ) is 2β (say, the number is four in Fig. 5, where β = 2). The locations of the peaks of the stripes move with time, the magnitudes of the peaks also change with time.
As before, when all the particles are given in the same ψ init initially and the interaction is ignored, the above formulae and discussion hold also for N-particle systems.
When the interaction is taken into account, the total Hamiltonian is H = ∑ iĥ i + ∑ i< jVij, where Vij = gδ (θ i − θ j), g = g↑ ↑ (if both atoms are up), g↓ ↓ (both down), or g↑ ↓ (one up and one down). In order to evaluate the effect of interaction in the simplest way, we study a two-body system. Firstly, a set of single particle states
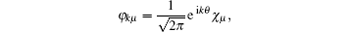
where 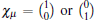
Note that the strength of a pair of realistic Rb atoms is gRb = 7.79 × 10− 12 Hz· cm3 (the differences in the strengths between the up– up, up– down, and down– down pairs are very small and are therefore disregarded). Since the atoms in related experiments are not distributed exactly on a one-dimensional ring but in a domain surrounding the ring, the effect of the diffused distribution should be considered. Hence, for each φ kμ we define its three-dimensional (3D) counterpart
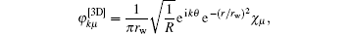
where the Gaussian function e− (r/rw)2 describes the diffused distribution and rw measures the width of the distribution. With 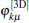
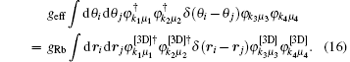
Then, we have
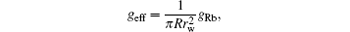
which is the effective strength adopted in our calculation.
It is assumed that both atoms are given at the same superposition state with ϕ = π or 0 initially. When the Hamiltonian is diagonalized in the space expanded by Φ i, the eigenenergies El and eigenstates Ψ l ≡ ∑ iCliΦ i can be obtained, and the time-dependent state is
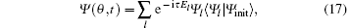
where Ψ init = ψ init(1)ψ init(2). From Ψ (θ , t) the densities and Pz(t) can be calculated. An example with kmax = 14 is shown in Fig. 6 where the strength g is given at three values. When kmax is changed from 14 to 12, there are no explicit changes in the pattern. It implies that the choice kmax = 14 is sufficient in qualitative sense.
 | Fig. 6. Pz of a two-body system of Rb atoms versus τ with interaction Vij = gδ (θ i − θ j), g = 0 (solid), 100geff (dash), and 2000geff (dash– dot). The initial state has ϕ = π (a) and ϕ = 0 (b). 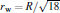 |
In Fig. 6 the curves “ 1” and “ 2” overlap approximately. It implies that the effect of interaction with a g ≤ 100geff is very small. However, when g = 2000geff, the amplitude decreases with time explicitly as shown by the dash– dot curve, while the period remains nearly unchanged. Note that, based on the Gross– Pitaevskii equation, the effect of the combined interaction imposing on a single particle from the other N − 1 particles is similar to an appropriate strengthening of the strength of the atom– atom interaction. Thus the explicit dampening that happens when g = 2000geff implies that, for an N-body system with a larger N, the dampening would actually occur. This is a topic to be clarified further. In fact, the dampening of the oscillation has already been observed in all related existing experiments.[16, 21]
In summary, the oscillation of the cold atoms under the SOC and constrained on a ring has been studied analytically without taking the interaction into account. Then, the effect of the interaction is evaluated numerically via a two-body system. Two cases, namely, the evolution that starts from a g.s. and is induced by a sudden change of the laser field, and the evolution that starts from a superposition state, are involved. The emphasis is placed on clarifying the relation between the parameters of the laser beams and the period and amplitude of the oscillation. This is achieved by giving a set of formulae so that the relation can be understood analytically. The conditions that the frequency and/or the amplitude can be maximized or minimized have been predicted. To realize the mutual-transformation of the two components, not only the strength of the Raman coupling γ is important, the energy difference between the two components is also important which can be tuned by δ (this is similar to the case of a resonance). The frequency of oscillation will increase with γ in general, while the amplitude depends on the inter-relation of γ and δ . When (δ , γ ) vary along a specific straight line on the δ – γ plane, the amplitude may increase, decrease, or even remain unchanged depending on the slope of the line. This is a common feature for the first case and for the second case with ϕ = π or 0, whereas when ϕ ≠ π and 0, movable stripes will emerge on the ring. Experimental confirmation of the regularity unveiled in this paper and the predicted phenomena is expected.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|