A quantum system is exactly solvable (ES) if all the eigenvalues and the corresponding eigenfunctions can be calculated in an exact analytical manner. ES models have attracted much attention because of their important applications in various branches of physics and mathematics. However, such systems are very rare and the Schrö dinger equation can be solved exactly only for a few number of potentials. In contrast, a quantum system is quasi-exactly solvable (QES) if only a finite number of eigenvalues and eigenfunctions can be determined exactly.^{[1– 6]} The QES models have received great attention due to their interesting mathematical structure and their role in applied fields.^{[7– 13]} These models are distinguished by the fact that their Hamiltonian preserves a finite-dimensional vector space of polynomials which can be written as a block diagonal matrix with at least one finite block. The eigenvalues and eigenfunctions corresponding to this block can always be calculated in an exact manner. During the past decades, the perturbed Coulomb potential has been the subject of much research in both relativistic and nonrelativistic regimes.^{[14– 28]} A very important example in this field is the Killingbeck potential

which plays an important role in many branches of physics including particle physics, ^{[29, 30]} quantum field theory, ^[31] molecular, ^{[32– 34]} and solid state physics.^{[35, 36]} Until now, a variety of techniques including the supersymmetric quantum mechanics, ^[37] the moment method, ^[22] the shifted 1/N expansion, ^{[15, 16]} the Hill determinant, ^{[17, 18]} the differential quadratic, ^[38] and the asymptotic iteration techniques^[39] have been used to deal with the potential. On the other hand, considerable efforts have been made to study the D-dimensional quantum mechanical systems with spherically symmetric potentials.^{[40– 42]} In this work, using the QES Lie-algebraic approach, we present a simple formalism for the D-dimensional Schrö dinger equation with the Killingbeck potential and find a finite number of exact solutions in the representation space of sl(2).

The rest of this paper is organized as follows. In Section  2, we briefly recall the general definition of QES differential equations. Section  3 is devoted to the algebraization of the D-dimensional Schrö dinger equation with the Killingbeck potential where we demonstrate that the system possesses a hidden sl(2) algebraic structure responsible for the QES structure. In addition, using the representation theory of sl(2), we obtain the exact expressions for the energies and the corresponding wavefunctions as well as the allowed values of the potential parameters. We finish the work with our concluding remarks in Section  4.

A linear differential operator H in a Hilbert space H is called QES if it leaves invariant a nontrivial finite-dimensional subspace P ⊂ H

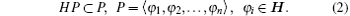
Then, the first n eigenvalues and the corresponding eigenfunctions can be obtained exactly by diagonalizing the corresponding matrix of the restricted action of H to the subspace P. Two spaces P and P̃ are equivalent if there exists a smooth non-vanishing gauge function G(x) such that

In this case, H̃ is equivalent to the H under the transformation given by

Since the transformed operator H̃ preserves the eigenvalue of H̃ P̃ = EP̃ and leaves the polynomial space P̃ _{n+ 1} invariant, it is therefore an element of the universal enveloping algebra U_sl(2) according to the Burnside' s theorem.^[43] In one dimension, the only Lie algebra of the first-order differential operators, which possesses finite-dimensional representations, is the sl(2) algebra, whose generators

leave invariant in the (n + 1)-dimensional linear space of polynomials in r (with at most degree n). Hence, the operator H̃ can be represented as a quadratic combination of the sl(2) generators as

In general, this operator does not have the form of a Schrö dinger operator but can be always reduced to a Schrö dinger-type operator by making a change of variable and a gauge transformation. In the next section, we apply the above method to obtain the eigenvalues and eigenfunctions as well as the allowed parameters of the Killingbeck potential for any given non-negative integer quantum number n.

In atomic units (m = ħ = c = 1), the D-dimensional Schrö dinger equation with spherically symmetric potential V(r) is given by

where the D-dimensional Laplacian operator is

Using the well-known technique of separation of variables and via

the radial part of the Schrö dinger equation becomes

Now, considering the potential in Eq.  (1), equation  (10) reduces to the following operator equation:

Making the gauge transformation

where

equation (4) gives

where we have multiplied the equation by r on the left for later convenience. We further simplify the equation by letting H̃ = rH̃ . In order to show how sl(2) Lie algebra underlies the QES of the problem, we consider the action of the operator H̃ on monomials of r. It is easy to verify that

which implies that the operator H̃ is not ES due to the existence of the r^{n+ 1} term. If this term vanishes from the right-hand side of Eq.  (15), the operator H̃ preserves a finite-dimensional subspace P̃ _{n+ 1} (r) which is related to quasi-exact solvability. Hence, the operator H̃ is QES with the invariant subspace P̃ _{n+ 1} (r). On the other hand, from Eq.  (6), any QES differential operator can be represented as

where C_{α β} , C_α , C ∈ R. Substitution of Eq.  (5) into Eq.  (16) yields the following differential form:

where P_i are the polynomials of degree i;

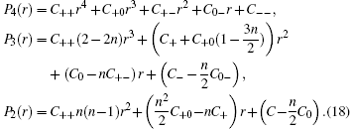
Comparing Eq.  (17) with Eq.  (14), we find

The exact energy eigenvalues for the Killingbeck potential are immediately obtained from the fourth equation in Eqs.  (19) as

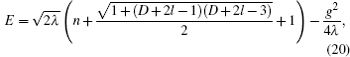
which reduces to the result of Ref.  [15] for the three-dimensional space. It is seen that the eigenvalues depend on five parameters λ , g, n, l, and D. It should be noted that these parameters are not independent of each other; rather they are connected by certain relations which will be discussed later. From Eqs.  (16) and (19), the Lie-algebraic differential operator H̃ ∈ U_sl(2) is written as follows:

Therefore, we have succeeded in obtaining the QES Schrö dinger equation with the Killingbeck potential which preserves the finite-dimensional subspace P̃ _{n+ 1} (r). As mentioned above, there exist important constraints on the potential parameters Z, λ , and g which differ for different values of n. Bessis et al.^[22] and Roychoudhury et al.^[15] obtained these constraints by means of the moment and shifted 1/N expansion methods, respectively. Now, with the help of the representation theory, we demonstrate that these constraints can be obtained in the framework of QES. For this purpose, we seek solutions of the operator H̃ restricted to the subspace P̃ _{n+ 1}. From Eq.  (21), the restriction of H̃ to P̃ _{n+ 1} is represented by an (n + 1)-dimensional matrix. Therefore, an (n + 1)-set of constraints on the potential parameters can be calculated algebraically by diagonalizing this matrix, which, together with Eq.  (20), gives the exact solutions of the problem. Since the operator H̃ in Eq.  (21) satisfies H̃ P̃ _{n+ 1} ⊂ P̃ _{n+ 1}, the corresponding eigenfunctions can be written as

which allows us to determine the (n + 1)-algebraic eigenfunctions. In the following, through sl(2) algebraization, we first determine the exact solutions for n = 0, 1, 2 and then generalize them to arbitrary n.

Case (i) n = 0

In this case, the operator H̃ possesses the invariant subspace P̃ ₁ (r) spanned by the basis {1}. Thus, the eigenfunction has the form and the corresponding matrix equation is given by

The nontrivial solution of this equation exists if the following relation among the potential parameters is satisfied:

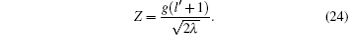
It is seen that when n = 0, there is a single relation between potential parameters. In other words, for any two of λ , Z, and g, there exists a unique value of the third parameter. Thus, from Eq.  (12), we obtain the ground-state wavefunction as

Case (ii) n = 1

In this case, the operator H̃ leaves the subspace P̃ ₂ (r) spanned by {1, r} invariant and the corresponding eigenfunction becomes . The corresponding matrix equation is therefore given by

The nontrivial solutions are obtained provided that

It is seen that for any two of λ , Z, and g, there exist two possible values of the third parameter. From Eqs.  (26) and (27), we obtain

Therefore, by using Eq.  (12), the wavefunction of the first excited-state can be written as

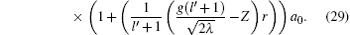
Case (iii) n = 2

In this case, the operator H̃ possesses the invariant subspace P̃ ₃ (r) with polynomial basis {1, r, r²} and the corresponding eigenfunction has the form . The corresponding matrix equation therefore becomes

From the condition of  nontrivial  solution of Eq.  (30), the potential parameters satisfy the constraint condition

where

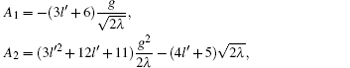
It is seen that for any two of λ , Z, and g, there exist three possible values of the third parameter. Thus, the wavefunction for the second excited-state can be written as

where

Following this method, an (n + 1)-set of exact solutions can be generated for an arbitrary n, as follows.

Case (iv) arbitrary n

In this case, the operator H̃ has a finite-dimensional invariant subspace P̃ _{n+ 1} (r), which is spanned by the basis {1, r, r², … , rⁿ}. Similarly, by considering the eigenfunction Eq.  (22), one can obtain the following matrix equation:

which is a generalization of Eqs.  (23), (26), and (30). It should be noted that this relation reduces to the results obtained in Refs.  [15] and [22] when D = 3 and l = 0, respectively. For a nontrivial solution to exist, the determinant  of the coefficient  matrix  must vanish which yields the constraints on the potential parameters. In this case, for any given non-negative integer n and two of λ , Z, and g parameters, there exist (n + 1) different values of the third parameter which correspond to the radial quantum numbers n_r = 0, 1, 2, … , n. Thus, the wavefunction for the n-th excited-state is given by

where the coefficients a_m satisfy the recursion relation

with the boundary conditions a_{− 1} = 0 and a_{m+ 1} = 0. Some of the numerical results obtained for the ground, the first, and the second excited states are displayed in Table  1. We use the parameter set given in Ref.  [15] for further comparison. It is observed that our results are exactly identical with those obtained in Ref.  [15]. Also, it is noted that our method reproduces the results of Ref.  [18] by choosing an appropriate set of parameter values. In Figs.  1– 3, the variations of energy as a function of dimension are plotted for n = 0, 1, 2. The corresponding unnormalized wavefunctions with initial condition a₀ = 1 are plotted in Fig.  4. It is seen from Figs.  1– 3 that when l = 0, the energy is symmetric with respect to D = 2 for 0 < D < 4. This is a common property of the s-wave energy spectrum irrespective of the quantum number n and can be explained by calculating the first derivative of the energy with respect to the dimension D. From Eq.  (20), the first derivative ∂ E/∂ D involves the term proportional to D + 2l − 2 which implies that for l = 0, equation  (20) has a turning point at D = 2.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Plots of energy versus D for n = 0 and various values of l.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Plots of energy versus D for n = 1 and various values of l.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Plots of energy versus D for n = 2 and various values of l.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Plots of wave function versus r for l = 0 and n = 0, 1, 2 in three dimensional space.

Table 1.

Table 1.

Table 1. Eigenenergies of the ground, the first, and the second excited states for λ = 0.1 and Z = 1 in three-dimensional space. nr l g E 0 0 0.44721 0.17082 0 1 0.22361 0.99303 0 2 0.14907 1.50969 1 0 0.09620 1.09490 0 0.57462 0.29256 1 1 0.00969 1.56501 0 0.36298 1.23586 1 2 − 0.02025 2.01144 0 0.28113 1.81488 2 0 − 0.10976 1.53513 1 0.24531 1.41481 0 0.68434 0.39443 2 1 − 0.15147 1.95511 1 0.15464 1.95268 0 0.48131 1.43331 2 2 − 0.15959 2.39632 1 0.11397 2.42720 0 0.39533 2.06856

Table 1. Eigenenergies of the ground, the first, and the second excited states for λ = 0.1 and Z = 1 in three-dimensional space.

By using the Lie algebraic approach of QES, we investigate the algebraic solutions of D-dimensional Schrö dinger equation with Killingbeck potential. We demonstrate that the corresponding equation is reducible to a QES differential equation with sl(2) hidden algebraic structure. With the help of the representation theory, we obtain expressions for the energies and wavefunctions as well as the allowed values of the potential parameters through the sl(2) algebraization. We also show that our results are identical to those obtained by other methods. It is found that the quasi-exact Lie algebraic approach is a powerful method of reproducing the exact analytical results.