†Corresponding author. E-mail: junyu@usx.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11275129).
Starting from the Davey–Stewartson equation, a Boussinesq-type coupled equation system is obtained by using a variable separation approach. For the Boussinesq-type coupled equation system, its consistent Riccati expansion (CRE) solvability is studied with the help of a Riccati equation. It is significant that the soliton–cnoidal wave interaction solution, expressed explicitly by Jacobi elliptic functions and the third type of incomplete elliptic integral, of the system is also given.
Nonlinear partial differential equations (PDEs) such as the Korteweg de-Vries and sine-Gordon models appear in almost all the branches of physics, especially, in the fluid mechanics, plasma physics, optical fibers, and solid state physics.[1] It is always an interesting topic to search for new exact solutions of nonlinear PDEs.[2– 5] So far, there are some marvelous approaches to solve this problem. Among them, the inverse scattering transformation, [6] the Darboux transformation, [7] the Hirota' s bilinear method, [8] and the symmetry analysis[9– 11] are all effective and valuable. However, these usual methods might lose some essential information of the original nonlinear PDEs and only some special solutions can be obtained. Thus it is necessary to establish an easy and understandable method to construct exact solutions for the nonlinear system. Recently, Lou[12] proposed a consistent Riccati expansion (CRE) method, which can be considered as an extension version of the usual Riccati equation method and the tanh function expansion method, such that we could find new solutions of the nonlinear PDEs. Based on the new method, a model is defined CRE-solvable if it has a CRE. In Ref. [13], we applied this method to the Gardner equation and found it is CRE-solvable, furthermore, the soliton– cnoidal wave interaction solution of the Gardner equation was also obtained.
As is well known, the Davey– Stewartson (DS) equation is an important nonlinear model, it can be written in some variant but equivalent forms[14] as follows:
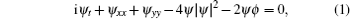
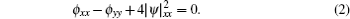
The system is the shallow water limit of the Benney– Roskes equation, [15] where ψ is the amplitude of a surface wavepacket and ϕ characterizes the mean motion generated by this surface wave. Equations (1) and (2) can also be obtained from the suitable reduction of a self-dual Yang– Mills equation.[16]
Introducing new dependent variables F (real) and G (complex) by
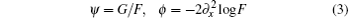
and rotating the coordinate axes by 45° , equations (1) and (2) can be written as
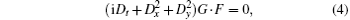
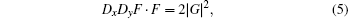
where D is the usual bilinear operator defined by
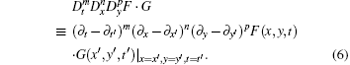
In Ref. [17], Lou and Lu solved the DS equation system (4) and (5) by means of a variable separation procedure. From the trivial solutions of Eqs. (4) and (5), G = 0 and DxDyF· F = 0, we may get a hint about their nontrivial solution (G ≠ 0):
F and G can be assumed to possess the following two variable separation forms,
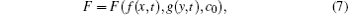
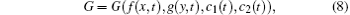
where f = f (x, t) and g = g(y, t) are y- and x-independent, c0 is an arbitrary constant, c1 = c1(t) and c2 = c2(t) being integration functions of time t.
After a tedious calculation, equations (4) and (5) can be reduced to the following two trilinear differential equations, [17]
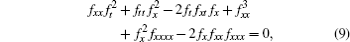
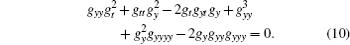
Actually, equation (10) possesses the same form as Eq. (9) simply by the transformation g → f, y → x. This symmetry is a natural result of the fact that equations (4) and (5) are symmetric with respect to space variables x and y. The integrability of Eq. (9) is guaranteed by the integrability of the DS equation.
Using the transformations 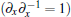
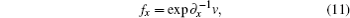
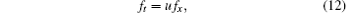
the trilinear form (9) can be changed to a Boussinesq-type coupled equation system
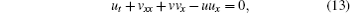
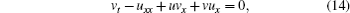
where equation (14) is obtained by differentiating Eq. (12) twice with respect to x. Once the multisoliton solutions of Eqs. (13) and (14) are obtained, the corresponding multidromion solutions of the DS equation can be obtained. So, the study on Eqs. (13) and (14) is very meaningful. Using a simple nonstandard truncated expansion and quite a universal reduction function, some new exact solutions for the Boussinesq-type coupled equation system were obtained.[18]
The aim of the present work is to find the CRE solvability and get some new solutions for the Boussinesq-type coupled equation system. In Section 2, the CRE is used to obtain the solvability of the system, and a soliton– cnoidal wave interaction solution of the system is given in the subsequent section. Section 4 contains a short discussion of our results.
For a given nonlinear partial differential equation,
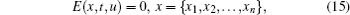
we aim to find the following possible truncated expansion solution
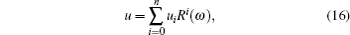
where R(ω ) is a solution of the Riccati equation
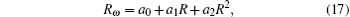
n is determined from the leading order analysis of Eq. (15). We can obtain ui after substituting Eq. (16) with Eq. (17) into Eq. (15) and vanishing the coefficients of the powers of R(ω ).
If the system for ui (i = 0, 1, 2, … , n) and ω obtained by vanishing all the coefficients of the powers of R(ω ) after substituting Eq. (16) with Eq. (17) into Eq. (15) is consistent, or not over-determined, we say the expansion (16) is a CRE and the nonlinear system (15) is CRE-solvable.[12]
Here, we apply the CRE method to the Boussinesq-type coupled equation system. As a result, we find it is CRE-solvable.
According to the leading order analysis, the exact solutions of Eqs. (13) and (14) have the following form
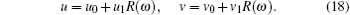
Substituting Eqs. (18) and (17) into Eqs. (13) and (14) respectively, we obtain
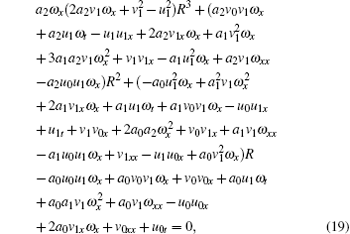
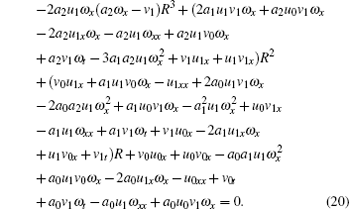
Setting zero for the coefficients of all the same powers of R in Eqs. (19) and (20), we have
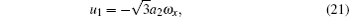
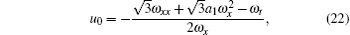

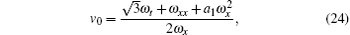
with the ω equation

where 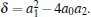
Finally, all the coefficient of R0 is zero. Evidently, the above condition is satisfied, thus equations (13) and (14) are CRE-solvable. In a word, we have the following theorem.
Theorem 1 If ω is a solution of Eq. (25), then
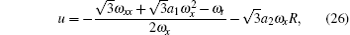
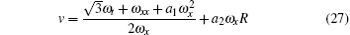
are the solutions of Eqs. (13) and (14) with R ≡ R(ω ) being the solution of the Riccati equation (17).
The next thing is to find the interaction solution of Eq. (25) with respect to ω . As mentioned in Ref. [12], the ω solutions characterizing the interactions between a soliton and a cnoidal wave for Eqs. (13) and (14) possess a form
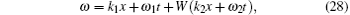
whereW(k2x+ ω 2t) = W(ξ ) ≡ W satisfies
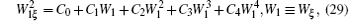
with
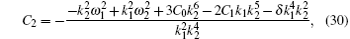
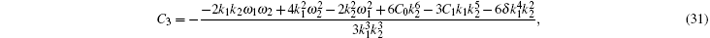
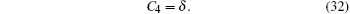
while the other constants ω 1, ω 2, k1, k2, C0, C1, and δ are all free.
Obviously, equation (29) is an equation for the definition of the elliptic functions which can be expressed by many elliptic functions such as the Jacobi elliptic cn(ξ ), sn(ξ ), and dn(ξ ) functions. So we can write down the soliton– cnoidal wave interaction solution with

where sn(z, m) is the usual Jacobi elliptic sine function and Eπ (ζ , n, m) is the third type of incomplete elliptic integral. Substituting Eq. (33) into Eq. (25), the soliton– cnoidal wave interaction solution for u of Eq. (26) is obtained
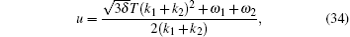
where k1, k2, ω 1, ω 2, and δ are free,
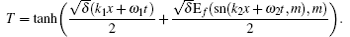
Finally, we discuss two special types of soliton– cnoidal waves for Eqs. (13) and (14) by selecting different constants for the solution (34).
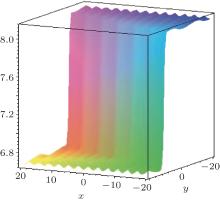
Figure 1 exhibits the first type of special soliton– cnoidal wave structure of u determined by Eq. (34) for Eqs. (13) and (14), with the parameters being selected as
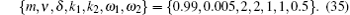
It also shows a particular periodic-kink wave interaction for Eqs. (13) and (14), in this case, the modulus is close to 1.
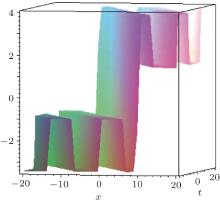 | Fig. 1. The first type of special soliton– cnoidal wave interaction solution for a Boussinesq-type coupled equation system given by Eq. (34) with the parameter selections (35). |
Figure 2 is the second type of the soliton– cnoidal wave interaction structure of u determined by Eq. (34) for Eqs. (13) and (14), with the parameters determined as
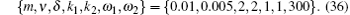
It also reveals the second type of the periodic-kink wave interaction solution for Eqs. (13) and (14), while the modulus m is taken as approaching to 0.
With the help of the Riccati equation, a Boussinesq-type coupled equation system is solved by the CRE method and its interaction among different nonlinear excitations is also found out. In particular, the soliton– cnoidal wave interaction solution is explicitly expressed by Jacobi elliptic functions and the third type of incomplete elliptic integral.
It is proved by our research that many integrable models such as the modified Korteweg de-Vries equation, Ablowitz– Kaup– Newell– Segur (AKNS) system, (2+ 1)-dimensional Konopelchenko– Dubrovsky equation, modified asymmetric Veselov– Novikov system are all CRE-solvable though not all the nonlinear PDEs are CRE-solvable. Therefore, the CRE method can be further used to check other integrable properties. The CRE method and the associated ω equation are worth studying further.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|