†Corresponding author. E-mail: xzwang696@126.com
*Project supported by the National Natural Science Foundation of China (Grant No. 11074061).
We present a modified method to solve the surface plasmons (SPs) of semi-infinite metal/dielectric superlattices and predicted new SP modes in physics. We find that four dispersion-equation sets and all possible SP modes are determined by them. Our analysis and numerical calculations indicate that besides the SP mode obtained in the original theory, the other two SP modes are predicted, which have either a positive group velocity or a negative group velocity. We also point out the possible defect in the previous theoretical method in accordance to the linear algebra principle.
Metallic superlattices (SLs) composed of alternating layers of two different metals first appeared in the late 1980s, [1– 3] and scientists found their unique magnetic property and conductivity (the inter-layer antiferromagnetic-exchange coupling and giant magneto-resistance).[2, 4– 6] These findings have opened up a new technological field and laid the foundation of spin electronics. Metal photonic crystals or metamaterials began to attract the attention of scientists in the 1990s.[7] Their surprising optical properties can lead to a large number of technological applications in optical– electron and optical– detection fields, so these metal structures have been received increasing attention.[8] It has been well-known that these properties mainly originate from the interaction between incident electromagnetic waves and plasmons in these structures.[9– 11] One-dimensional photonic crystals, or say the superlattices, composed of alternating layers of metals and dielectrics are the simplest example of these structures. It is just a metal-layer array in air when the dielectric layers are of air. The earliest research about plasmons of the metal/dielectric SLs was done by Mills and Camley.[12, 13] For the semi-infinite metal-layer arrays, the conclusion obtained by them is that the surface plasmons (SPs) exist only if the metal layers are thicker than air spacers and the SP frequency is the same as that of the semi-infinite metal. After which, the plasmons in the finite-thickness SL were discussed[14] and then the magnetoplasmons and plasmon polaritons in the same structure were investigated.[15– 17] However, we find that there is a defect in the previous SP theory for the semi-infinite SLs, and so a re-discussion is necessary. In fact, the similar problem also exists in the previous theory of the surface plasmon polaritons in this SL. In this paper, a modified theory is presented to re-solve the SPs of the semi-infinite metal/dielectric SLs and new SP modes are predicted.
The SL structure and the coordinate system are shown in Fig. 1, where dm and dd are the thicknesses of metal and dielectric layers, and the SL period L = dm + dd. We propose that the layers are thick enough to be characterized by bulk dielectric function ε m and bulk dielectric constant ε d, respectively, ε c is the dielectric constant in the upper half space.
In this paper, we discuss only the SPs and do not discuss the SP polaritons, so the retarded term in the Maxwell equations is ignored. As a result, the plasmon-wave equation is ∇ · D = 0, where the electric displacement D = ε E and electric field E = − ∇ φ with the electrostatic potential φ . We propose that the SP propagates along the y axis and exponentially attenuates along the x axis. According to the wave equation, we directly write the electrostatic potential in the upper semi-space and the first SL period as follows:



where the indexes m, d, and c indicate the metal and dielectric layers, and upper medium, respectively, k is the wave-number along the y axis, Aj and Bj (j = 0, + , − ) denote the amplitudes of the electrostatic potential. We should note that the potential in the second period is equal to the product of the first-period potential and e− Γ L. Using the boundary conditions of φ and Dx continuous at the surface, the first and second interfaces, we find the following relations among the potential amplitudes:



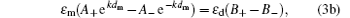
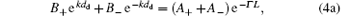

where Γ is the attenuation coefficient of the SPs and must be real and positive when the metal dielectric function is considered as a real number. The six equations make up a set of homogeneous linear equations of the amplitudes. It should be mentioned that this system contains only five amplitudes (or five linear unknowns). Indeed, for calculating the SP dispersion curves (ω ∝ k), there are six unknowns to be eliminated, but Γ is not a linear unknown. Thus the SP dispersion relations must be carefully derived to guarantee the existence of the SP wave solutions. In order to simply and intuitively obtain the features of the SPs and compare with the given results, [12] we set ε c = ε d = 1 and then the SL is just a metal-layer array in air.
The existence of non-zero solutions of unknowns A± and B± first require that the determinant of their coefficient matrix must be equal to zero, so according to Eqs. (3) and (4), we find a necessary dispersion equation

but it is not sufficient for solving the dispersion relation (ω ∝ k). The most critical question is how to find an additional equation to determine the attenuation factor Γ in Eq. (5). Although the above equation system include six unknowns (A0, A± , B± , and Γ ), Γ is not a linear unknown and is included in the coefficients of A± . Consequently, according to the linear-algebra principle, we can use only five equations in the system to determine the expression of Γ . According to Eq. (2), we obtain
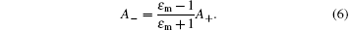
Selecting three equations from Eqs. (3) and (4), we have four selections. The first selection, using Eqs. (3) and (4a), leads to
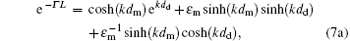
and the second choice is to take Eqs. (3) and (4b), we obtain
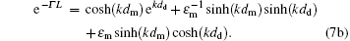
We obtain the third expression from Eqs. (3a) and (4), that is

and finally we find the forth expression from Eqs. (3b) and (4) that

Now, we discuss the above four equations. First, we consider two important limit cases, dd → 0 and dd → ∞ . In the first case, the array becomes a semi-infinite bulk metal. It is obvious that equations (7a)– (7d) all can be changed into
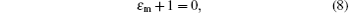
since equation (5) leads to Γ = k in this case. It is just the SP dispersion relation of the bulk metals. In the second case, equations (7a)– (7d) directly lead to

or equivalently

which is just the dispersion relation of the SPs in an isolated metallic film. Therefore, we conclude that our theory is available in the limit cases.
In general case, we find that equation (8) can always satisfy Eqs. (5) and (7) for Γ = k(dm − dd)/L simultaneously. As a result, in the condition of dm > dd, there is such a SP mode the same as that of the bulk metals, which is a given SP mode predicted in the previous work.[12] We study the four dispersion equation sets, composed of Eqs. (5) and (7a)– (7d), respectively. All of the possible SP modes of the array are determined by them. Equation (7) cannot be simultaneous, otherwise it will be inconsistent with the linear algebra principle.
Next, we will discuss the previous theory.[12] Although the authors corrected some shortcomings, [13] there is still a defect. Their equations (2.35) and (2.36) in Ref. [12] are the dispersion relations of the SPs. If we imagine that the dielectric layers in and medium above the SL are the same, equation (2.35) has no significance both in mathematics and physics, successively, the final dispersion equation (2.38) is also questionable. In addition, for the metal-layer arrays (or ε B = ε c = 1), it is difficult to understand why there is only an SP mode the same as that of the bulk metals. The SPs of the array should originate from the coupling of SPs in metal layers. As we know, the SPs of a single metal film has two modes changing with wave number, so we believe that there should be SP modes changing with wave number in the array.
The bulk-plasmon dispersion relation can be obtained by the replacement Γ → iQ in Eq. (5), where Q is the Bloch wave vector. The dispersion relation is written as
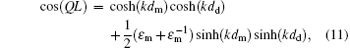
which is useful for discussing the SPs of the array.
In this section, we solve the four dispersion-equation sets numerically. Though the dielectric function of metals is usually expressed as 

which seems better for actual metals.[18, 19] The physical parameters are taken as ω p = 1.419 × 1016 rad/s (75280 cm− 1), ε ∞ = 4.017, and ε 0 = 4.896, which are closed to those of sliver.[18, 19] The array period is fixed at L = 1.0, equivalent to about 133 nm, k in the dispersion relations always appears in the style kdm or kdd, so the increase of k should cause the same effect as that resulting from the enlargement of L. The wave number and frequency are measured in ω p.
 | Fig. 2. Dispersion curves of SP of the metal-layer array. Besides Eq. (5), panels (a)– (d) are related to Eqs. (7a)– (7d), respectively. The horizontal purple lines in panels (a) and (b) are the given mode. The dot lines in panels (c) and (d) mean dm = 1. The dot lines show the SP mode of the bulk metals with frequency of 0.418ω p. |
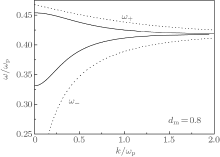
In calculations, besides the given SP mode existing under the condition of dm > dd, we find that the four equation sets always offer two additional SP modes. For example, there are three SP modes for dm ≥ dd, as illustrated in Figs. 2(a) and 2(b). The two new SP modes seen here are situated above and below the given SP mode, respectively. The higher-frequency and lower-frequency modes have a negative group velocity and a positive group velocity, respectively, whose frequencies approach to 0.418, that of the bulk-metal SP, in the large-wave number limit. For dm < dd, only two additional SP modes are shown in Figs. 2(c) and 2(d), where the given PS mode disappears. Comparing the curves obtained in the cases of dm > dd and dm < dd, we find that the two additional modes possess the invariance as the air- and metal-layer thicknesses are exchanged. For example, the two modes in the cases of dm = 0.2 and dm = 0.8 are the same.
 | Fig. 3. SP dispersion curves of the array and the single metal film, the dot curves are those of the film and the solid curves represent the two SP modes of the array. |
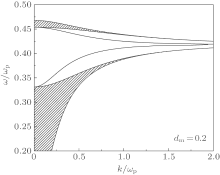 | Fig. 4. SP modes and bulk plasmon continua of the array. The solid curves indicate the surface plasmon modes and the shadow areas are the bulk continua. |
We also compare the SP modes of the array with those of the single metal layer (metal film), as illustrated in Fig. 3. It is indicated that the SP higher- and lower-frequency modes in the SL are closed to the top and bottom SP modes (ω ± ) of the film, respectively. From this figure, we estimate that the low-frequency mode comes from the coupling of the bottom surface modes in metallic layers and the high-frequency mode comes from the coupling of the top surface modes.
Finally, we examine the relation between the SPs and bulk plasmons. Their dispersion properties are illustrated in Fig. 4 with the same parameters as those in Fig. 3. We see that the two additional modes of the SPs both appear in the forbidden-band of bulk plasmons, extending out from the boundaries of the bulk continua.
We re-discussed the surface plasmons of the metal-layer array and corrected the given theory and obtained new dispersion equations and numerical results. The four simultaneous dispersion equation sets, composed of Eqs. (5) and (7a)– (7d), respectively, determine the dispersion properties of the surface plasmons. Unlike the results given in the previous work, where only the surface plasmon mode exists in the condition of dm > dd and its frequency is equal to that of the surface plasmons of the bulk metal, in this paper the surface plasmons of the array possesses two additional modes. The three surface plasmon modes exist in the case of dm > dd, and the two modes appear in the situation of dm < dd. The surface plasmons of the array are a kind of collective excitation and originate from the coupling of surface plasmons in adjacent metal layers in the array. The additional surface plasmon modes have the invariability as the metal-layer and the air-layer thicknesses dm and dd are exchanged.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|



