Cite this Article
Shao Wei-Hang, Chen Wei-Zhong†. Effect of supercritical water shell on cavitation bubble dynamics* . Chinese Physics B, 2015, 24(5): 054701  
Permissions
Effect of supercritical water shell on cavitation bubble dynamics*
Shao Wei-Hang, Chen Wei-Zhong†
The Key Laboratory of Modern Acoustics, Nanjing University, Nanjing 210093, China

†Corresponding author. E-mail: wzchen@nju.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11174145 and 11334005).

Abstract

Based on reported experimental data, a new model for single cavitation bubble dynamics is proposed considering a supercritical water (SCW) shell surrounding the bubble. Theoretical investigations show that the SCW shell apparently slows down the oscillation of the bubble and cools the gas temperature inside the collapsing bubble. Furthermore, the model is simplified to a Rayleigh–Plesset-like equation for a thin SCW shell. The dependence of the bubble dynamics on the thickness and density of the SCW shell is studied. The results show the bubble dynamics depends on the thickness but is insensitive to the density of the SCW shell. The thicker the SCW shell is, the smaller are the wall velocity and the gas temperature in the bubble. In the authors’ opinion, the SCW shell works as a buffering agent. In collapsing, it is compressed to absorb a good deal of the work transformed into the bubble internal energy during bubble collapse so that it weakens the bubble oscillations.

Keyword: 47.55.dd; 43.35.Ei; 43.25.Yw; supercritical water shell; bubble dynamics
1. Introduction

Research on the cavitation bubble dates back to the early 20th century, since the pioneering study of Lord.[1] Equations originally derived by Rayleigh and modified by later researchers describe the cavitation bubble dynamics well. Both the numerical results of these equations and the experimental outcomes, such as sonoluminescence, [2, 3] showed that the temperature runs up to thousands of Kelvin and the pressure reaches hundreds of bars inside the bubble during bubble collapsing.[4– 6] In 1979, the temperature and pressure inside the bubble were estimated at 3360  K and 313  atm (1  atm≃ 1  bar) respectively by comparing the experimental measurement with the theoretical derivation.[7] Later, in organic and polymeric liquids, the temperature was reported to exceed 5000  K inside the bubble.[8, 9] Then in the 1990s, when the single-bubble sonoluminescence was first reported, [2, 10] researchers found that by studying the spectrum of the light emitted by the bubble itself, the bubble can be treated as a black body with the effective bubble collapse temperature ranging from 6000  K to 25000  K.[11– 14]

Based on the results above, one might infer that the gas-liquid interface is not “ clean” but contains a layer of hot liquid gas that coexists in the bubble’ s oscillation. In 1986, Suslick et al. found that there are two regions of sonochemical reactivity: one corresponds to the gas phase within the collapsing cavity, and the other to a thin hot liquid layer surrounding the collapsing cavity.[15, 16] Furthermore, they determined experimentally the effective temperature, and calculated the thickness of this layer. In 1994, Hua et al. proposed that bubble collapse generates a layer of supercritical water (SCW) surrounding the bubble, since the temperature and pressure exceed the critical values of water.[17] They also presented experimental results on the kinetics of p-nitrophenyl acetate (p-NPA) hydrolysis in support of their hypothesis of the existence of SCW during ultrasonic irradiation in water.

Whether and how the SCW shell exists are interesting questions and worthy of further investigation. In the authors’ opinion, it is worth considering the existence of the SCW shell and studying its effect on the bubble dynamics. As we know, the SCW has physical characteristics intermediate between those of gas and liquid.[18] However, it is unsuitable to regard the SCW as a part of the gas or the liquid since:[19] (i) the density of the SCW is much larger than that of gas; (ii) the SCW has much better condensibility than the liquid. What is more, the viscous coefficient of the SCW is about an order of magnitude smaller than that of the liquid (water). Therefore, the free cavitation bubble models which only contain two regions, the inner gas and the outer liquid, can hardly describe the role of the SCW in bubble dynamics. Therefore, by reference to models for the encapsulated bubble, [20, 21] we construct a three-layer model (gas-SCW-liquid) for the cavitation bubble to study the influence of the SCW shell on bubble dynamics.

In the next section, we will introduce the three-layer model based on the hydrodynamics and thermodynamics. We will analyze this model numerically and reveal the effect of the SCW shell on bubble dynamics covered in Sections  3 and 4. In Section  5, we will simplify this model and derive a Rayleigh– Plesset-like equation for the case of a thin SCW shell. Then we will study the dependence of bubble dynamics on the thickness and density of the SCW shell. In the last section, we will summarize the main results.

2. Model for cavitation bubble covered with SCW shell

Before introducing the model, some necessary discussion should be addressed. As introduced before, during bubble collapse, the pressure and temperature inside the bubble are extremely high so that a layer of liquid surrounding the bubble may turn out to be supercritical water. In this model, we do not talk about the generation of the SCW layer, but focus on investigating the effect of the SCW layer on the bubble dynamics, that is, the bubble dynamics on the stage when the SCW layer has already existed and both mass and heat exchanges among the inner gas, the SCW layer and the outer liquid have already reached their dynamic equilibriums. At this stage, the mass diffusion, the heat conduction, and the phase transition do not accumulate with time, and considering the bubble oscillates at high frequency, they are small during a single acoustic cycle.[22– 25] Then the SCW layer is almost like a bubble shell which traps the gas inside the bubble. Hence, in this paper, we ignore mass and heat exchanges in our model for simplification.

We consider a cavitation bubble levitated in liquid driven by ultrasound. This system can be divided into three layers: the gas inside the bubble, the liquid outside the bubble, and the interface layer of the SCW (see Fig.  1). For each layer, we will discuss its dynamic equations respectively in the following.

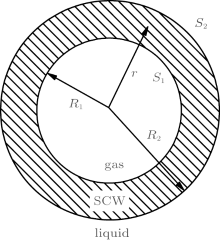Fig.  1. A sketch of the three-layer (gas-SCW-liquid) model for cavitation bubble. S1 and S2 denote the inner and outer spherical boundaries with radii R1 and R2, respectively.

2.1. The SCW layer (shell)

In the absence of body force and viscous damping, the dynamic constitutive equation in the SCW shell is

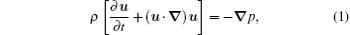
where u, p, and ρ are the velocity, pressure, and density of the SCW shell in position r at time t, respectively. We ignore the mass exchange of the SCW shell with the inner gas and outer liquid, that is to say, the mass of the SCW shell is assumed to be invariable, so we have the continuity equation

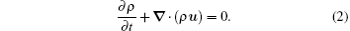
Since the layer of the SCW is thin compared to the radius of the bubble, [15] in our model, we suppose that this layer is uniform in density so that ρ = ρ (t) is independent of the position r. So for a spherical bubble, equation  (2) can be rewritten as

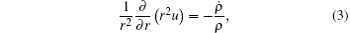
so u(r, t) has the general solution form

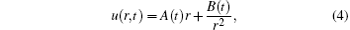
where A(t) and B(t) are functions of t, and

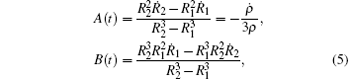
with Ṙ 1 = u(R1, t) and Ṙ 2 = u(R2, t). Integrating Eq.  (1) from R1 to r yields

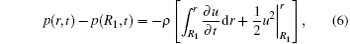
then we substitute Eq.  (4) into Eq.  (6) and obtain

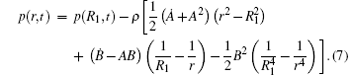
The state of the SCW shell satisfies the van der Waals equation[26]

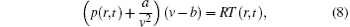
where T and v = mH2O/ρ are the temperature and molar volume of the SCW shell with the molar mass mH2O = 18  g/mol for water, R = 8.31  J· mol− 1· K− 1) is the gas constant, a = 0.5536  J· m3· mol− 2 and b = 3.049 × 10− 5  m3· mol− 1 are the van der Waals constants for water, respectively.

The elementary work đ W on the SCW shell can be calculated as follows:

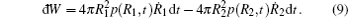
The heat exchange is ignored in our model, so the work leads to the increase of the energy E

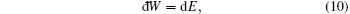
where the SCW shell energy E includes the kinetic energy

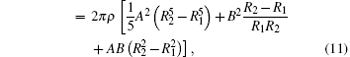
and the internal energy

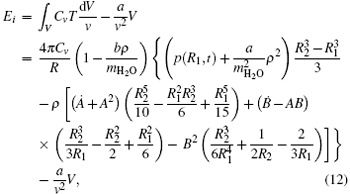
with the volume of the SCW shell 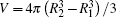and the molar heat capacity at constant volume Cv = 3R.[27, 28] As we know, equation  (10) is the energy equation of the SCW shell. Its concrete form is too long and complex to be presented here. Readers can obtain it by substituting Eqs.  (5), (7)– (9), (11), and (12) into Eq.  (10).

2.2. The liquid layer

Early models for the cavitation bubble treat the liquid as incompressible. Since the 1950s, more precise models including the compression correction have been given by Flynn, [29] Gilmore, [30] Prosperetti– Lezzi, [31] Keller– Miksis, [32] and so on. If we follow the derivation of Keller– Miksis, then we have

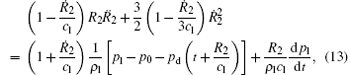
where pl is the pressure on the liquid side of the boundary S2, pd(t) is the driving ultrasound, p0 is the atmosphere pressure, and cl is the sound speed in liquid at the ambient temperature T0 = 293  K and pressure P0 = 1  atm, respectively.[28] The dynamical boundary conditions of the S1 and S2 stipulate that the discontinuity in the normal stress should equal the surface tension[33]

where pg is the gas pressure inside the bubble, η is the shear viscosity of the liquid, σ 1 and σ 2 are the surface tension coefficients at the interfaces S1 and S2, respectively.

2.3. The gas layer

As a simple model, we can take the temperature and pressure to be uniform within the bubble, [34] that is

with R10 and R20 being the ambient inner and outer radii of the bubble, h = R10/8.5 being the van der Waals hard core radius, and κ being the polytropic exponent, respectively. As discussed before, the mass and heat exchanges are small in our model and are reasonably neglected. Therefore, the gas inside the bubble can be treated as adiabatic, [22, 25] that is, κ = γ with γ = 1.4 being the adiabatic exponent, and the gas temperature is

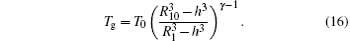
Combining the differential Eqs.  (10) and (13), we can calculate R1 and R2 numerically. Meanwhile, the temperature and the density of the SCW shell can also be worked out.

3. Effect of the SCW shell on bubble dynamics

Before the simulation, some parameters need to be assigned. (i) The driving pressure is set to be a sinusoidal wave that pd = pasin(2π ft) with the amplitude pa and frequency f. (ii) As we know, the SCW has very small surface tension compared to general liquids.[35] So we have σ 1 ≃ 0 and σ 2 ≃ σ 0 with σ 0 being the surface tension coefficient of the gas-liquid interface. In fact, 2σ 1/R1 + 2σ 2/R2≃ 2(σ 1 + σ 2)/R2≃ 2σ 0/R2, since the SCW shell is thin. In the simulation, we just let σ 1 = 0 and σ 2 = σ 0. (iii) The properties of the SCW shell, though they cannot be numerically identified in our model due to the lack of a discussion on the SCW shell generation, refer to the theoretical estimation and experimental data. So, the thickness of the SCW shell ranges from several decades to several hundreds of nm according to the estimation and experimental data.[15, 17] Also, the density of the SCW shell is much larger than ordinary gas but will not exceed 590.36  kg/m3 since b = 3.049 × 10− 5  m3/mol.[36]

Based on the SCW shell model, we simulate the dynamics of a real cavitation bubble using the self adaptive fifth-order Runger– Kutta arithmetic. Referring to the experimental conditions, we let the parameters be pa = 1.3  atm, f = 25  kHz, R20 = 4.55  μ m, R10 = 4.50  μ m, ρ (0) = 300  kg/m3, p0 = 1  atm, σ 0 = 0.076  N/m, and η = 0.0089  Pa· s, respectively.[37, 38] For comparison, we also use the no-shell model, that is, the Keller– Miksis (K– M) model, [32] to simulate the bubble dynamics with the ambient radius R0 = R10 with the other parameters being the same.

Figure  2 shows that the SCW model presents nearly the same R– t curve as the K– M model does except for an important difference in bubble collapse (see the inset), where the SCW model outputs a larger radius than the K– M model does. This reflects the drastic difference in the dynamics of bubbles with and without a SCW shell at the moment of collapse. Figures  3 and 4 respectively display the wall velocity and gas temperature as functions of time. In Fig.  3, we find the absolute value of the wall velocity in the SCW model is 600  m/s, which is obviously smaller than the 1200  m/s in the K– M model when the bubble collapses. That is to say, the Mach number | Ṙ /cl| becomes small due to the existence of the SCW shell, so that the shock wave generated during bubble collapse[36, 39] will be weakened. Accordingly, Figure  4 shows that in the bubble collapse, the temperature of the gas encapsulated by the SCW shell decreases by 1100  K compared with the 5100  K of gas without the SCW shell. These results show an obvious negative effect of the SCW shell on cavitation bubble dynamics. The mechanism of this effect, in our opinion, is that when the bubble collapses, the external liquid does positive work on the SCW shell and the internal gas to make their temperatures go up, and the SCW shell gains quite a lot of the work. Therefore, in collapsing, the kinetic energy of the bubble is weak and the temperature of the internal gas is relatively low due to the existence of the SCW shell. The SCW shell definitely slows down the oscillation of the bubble and cools the gas inside the bubble when the bubble collapses. Furthermore, it can be inferred that both the sonoluminescence intensity and the chemical reaction rates in gas will come down relatively.

Fig.  2. The R– t curves of bubbles with and without the SCW shell in an entire cycle. The inset magnifies the details of curves referring to the collapse of the bubble.

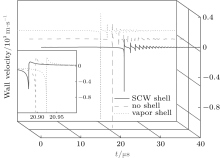Fig.  3. The wall velocity of bubbles with the SCW shell, no shell and the vapor shell in an entire cycle. The inset magnifies the details of curves referring to the collapse of the bubble.

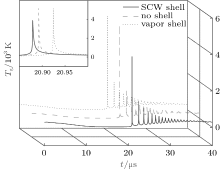Fig.  4. The gas temperature of bubbles with the SCW shell, no shell and the vapor shell in an entire cycle. The inset magnifies the details of curves referring to the collapse of the bubble.

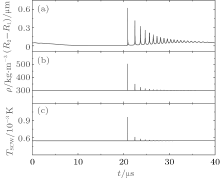
For examining the state of the SCW shell, we plot the evolution of the thickness, density, and temperature of the SCW shell, as shown in Fig.  5. The temperature is recorded as TSCW = [T(R1, t) + T(R2, t)]/2. The thickness of the SCW shell shrinks when the bubble expands, while it thickens during bubble collapse (see Fig.  5(a)). The density and temperature of the SCW shell almost remain unchanged with their initially set values 300  kg/m3 (= ρ (0)) and 546  K respectively except for some upheavals in the bubble collapsing and rebounding. Their peak values reach to about 500  kg/m3 and 1000  K at the moment of collapse (see Figs.  5(b) and 5(c)). These outcomes show the SCW shell maintains its hot and dense state for the whole period, which is quite different from the liquid and gas.

Fig.  5. The state of the SCW shell including thickness (a), density (b), and temperature (c) in an entire cycle.

4. Bubble covered with vapor shell

To understand the effect of the SCW shell in more detail, we replace the SCW with the vapor at normal temperature and pressure, and repeat the numerical calculation. The vapor is assumed to be under standard conditions (293  K, 1  atm, 22.4  L/mol) before driving so that its initial density is about 0.804  kg/m3. The other parameters are the same as those introduced in Section  3. As shown in Fig.  6, the R– t curve has almost no difference from that of a bubble without a shell. Even in the bubble collapsing, the two curves are very similar except for a tiny shift (see the inset). The wall velocity and gas temperature of the bubble with a vapor shell are quite different from those of the bubble covered by a SCW shell, while they are almost the same as those output by the K– M model (see Figs.  3 and 4). These outcomes tell us that a vapor shell has little effect on bubble dynamics.

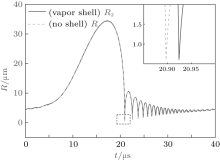Fig.  6. The R– t curves of bubbles with and without the normal vapor shell in an entire cycle. The inset magnifies the details of curves referring to the collapse of the bubble.

The state of the vapor shell is recorded in Fig.  7. We are surprised to see that the evolution of the shell thickness follows the R– t curve, that is, the vapor shell thickens when the bubble expands and shrinks when the bubble collapses, which is just the opposite of the behavior of the SCW shell (see Fig.  7(a)). Judging from Figs.  7(b) and 7(c), we see the values of the density and those of the temperature of the vapor range respectively from zero to hundreds and zero to thousands during bubble collapse, which just coheres with the characteristics of the gas inside the bubble. So based on these results, it is proved that the vapor shell can be regarded as a small part of the gas inside the bubble and it can hardly substitute the role the SCW shell plays in bubble dynamics.

Fig.  7. The state of the vapor shell including thickness (a), density (b), and temperature (c) in an entire cycle.

5. The influence of the SCW shell state on bubble dynamics

As mentioned above, the concrete form of Eq.  (10) is very long and complex. Fortunately, considering the SCW shell is very thin, ε (t) = (R2 – R1)/R2 ≪ 1, we can simplify equations by omitting the terms of high order in ε (t). Therefore, equation  (10) becomes

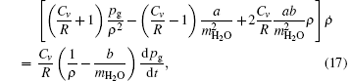
and equation  (13) changes to

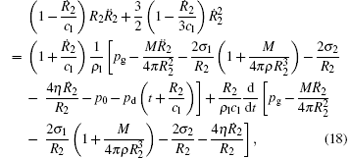
where

is the mass of the SCW shell and

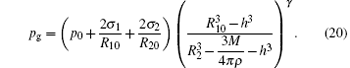
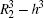
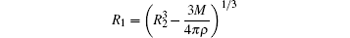
It is worth noting that equation  (20) cannot be expanded approximately any more since and 3M/(4π ρ ) are at the same magnitude when the bubble collapses. Combining Eqs.  (17) and (18), we can solve R2 and ρ , then

is obtained in the meantime. Numerical calculation shows that the simplified model has very little deviation from the original one if the thickness of the SCW shell is < 1  μ m.

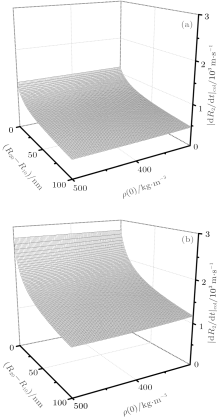
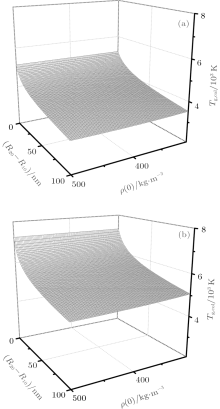
Based on this simplified model, we can easily analyze the relationship between the state of the SCW shell and bubble dynamics numerically. Calculations showed that the SCW shell mainly takes effect at the moment of collapse, so we focused on | Ṙ 2| col and Tg, col, the wall velocity and gas temperature at that time, and investigated their dependence on the thickness R20 – R10 and density ρ (0) of the SCW shell.

For two cases: pa = 1.3  atm and pa = 1.5  atm, we have computed the wall velocity and gas temperature at the moment of collapse, respectively. In the calculations, we chose the thickness and density of the SCW shell to range from 0 to 100  nm and 300 to 500  kg/m3, respectively. The other parameters are the same as before. Figures  8 and 9 respectively show the | Ṙ 2| col and Tg, col as functions of the thickness and density of the SCW shell. As we see, it is clear that the thicker the SCW shell is, the smaller are the | Ṙ 2| col and the Tg, col, so bubble dynamics depends on the thickness of the SCW shell. However, we also see the density of the SCW shell has a very weak influence on the bubble dynamics compared to the thickness. Its variation (increment) makes little change (decrement) to | Ṙ 2| col and Tg, col, despite the thickness. According to these results, the SCW shell works just as a buffering agent in a bubble’ s oscillation. When the bubble collapses, the SCW shell is well compressed, absorbing a good deal of the work transformed into the bubble internal energy, so, the kinetic energy of the bubble is weakened and the temperature of gas drops down. The larger volume of the SCW shell, the more energy it can take in. That is why bubble dynamics is sensitive to the thickness of the SCW shell.

Fig.  8. The dependence of the wall velocity in bubble collapsing | Ṙ 2| col on the initial thickness and density of the SCW shell. The driving amplitude is set to be (a) pa = 1.3  atm and (b) pa = 1.5  atm.

Fig.  9. The dependence of the gas temperature in bubble collapsing Tg, col on the initial thickness and density of the SCW shell. The driving amplitude is set to be (a) pa = 1.3  atm and (b) pa = 1.5  atm.

6. Conclusion

We have constructed a model of the cavitation bubble covered with a supercritical water (SCW) shell. Based on this model, we numerically studied the oscillation of bubbles in three ways: with a SCW shell, with a vapor shell, and without a shell. The results showed that the SCW shell effectively slows down the oscillation of the bubble and cools the gas temperature inside the bubble during bubble collapse. Apart from the SCW shell, the vapor inside the bubble is shown to have no remarkable effect on the bubble dynamics. We also found that the SCW gets thinner when bubble expands, while it thickens during bubble collapse. Besides, according to the numerical calculations, the values of the temperature and density of the SCW shell remain high and especially upheave during bubble collapse. In our further work, we simplified the model and derived the Rayleigh– Plesset-like equation for a thin SCW shell. The simplified model is numerically identified to have very little deviation from the original one, within a certain scale of the SCW shell thickness. We also studied the dependence of bubble dynamics on the thickness and density of the SCW shell. The outcomes tell that the bubble dynamics depends on the shell thickness. The thicker the SCW shell is, the smaller are the wall velocity and the gas temperature inside the bubble. However, the bubble dynamics is insensitive to the shell density. By our analysis, the SCW shell acts simply as a buffering agent to the motion of the bubble. When the bubble collapses, the shell is compressed, absorbing a good deal of the work transformed into the bubble’ s internal energy, so that it weakens the bubble’ s oscillation.

Reference
1 Lord R 1917 Philos. Mag. 34 94 DOI:10.1080/14786440808635681 [Cited within:1] [JCR: 1.596]
2 Crum L A 1994 Phys. Today 47 22 [Cited within:2] [JCR: 6.762]
3 Leighton T G 2001 The Acoustic Bubble London Academic [Cited within:1]
4 Xie C G, An Y and Ying C F 2003 Acta. Phys. Sin. 52 102(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
5 An Y 2008 Chin. Phys. B 17 2984 DOI:10.1088/1674-1056/17/8/037 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
6 An Y and Zhang W J 2012 Chin. Phys. B 21 017806 DOI:10.1088/1674-1056/21/1/017806 [Cited within:1]
7 Sehgal C, Steer R P, Sutherland R G and Verrall R E 1979 J. Phys. Chem. 70 2242 DOI:10.1063/1.437704 [Cited within:1]
8 Flint E B and Suslick K S 1989 J. Am. Chem. Soc. 111 6987 DOI:10.1021/ja00200a014 [Cited within:1] [JCR: 10.677]
9 Flint E B and Suslick K S 1991 Science 253 1397 DOI:10.1126/science.253.5026.1397 [Cited within:1]
10 Gaitan D F, Crum L A, Church C C and Roy R A 1992 J. Acoust. Soc. Am. 91 3166 DOI:10.1121/1.402855 [Cited within:1] [JCR: 1.646]
11 Hiller R, Putterman S J and Barber B P 1992 Phys. Rev. Lett. 69 1182 DOI:10.1103/PhysRevLett.69.1182 [Cited within:1] [JCR: 7.943]
12 Hiller R and Putterman S J 1995 Phys. Rev. Lett. 75 3549 DOI:10.1103/PhysRevLett.75.3549 [Cited within:1]
13 Hiller R and Putterman S J 1996 Phys. Rev. Lett. 77 2345 DOI:10.1103/PhysRevLett.77.2345 [Cited within:1] [JCR: 7.943]
14 Gaitan D F, Atchley A A, Lewia S D, Carlson J T, Maruyama X K, Moran M and Sweider D 1996 Phys. Rev. E 54 525 DOI:10.1103/PhysRevE.54.525 [Cited within:1] [JCR: 2.313]
15 Suslick K S, Hammerton D A and Jr Cline R E 1986 J. Am. Chem. Soc. 108 5641 DOI:10.1021/ja00278a055 [Cited within:3] [JCR: 10.677]
16 Suslick K S, McNamara III W B and Didenko Y 1999 “Hot Spot Conditions During Multi-Bubble Cavitation” in Sonochemistry and Sonoluminescence Dordrecht Kluwer Publishers [Cited within:1]
17 Hua I, Höchemer R H and Hoffmann M R 1995 J. Phys. Chem. 99 2335 DOI:10.1021/j100008a015 [Cited within:2] [JCR: 1.578]
18 Shaw R W, Brill T B, Clifford A A, Ecker C A and Franck E U 1991 Chem. Eng. News 69 26 [Cited within:1] [JCR: 0.284]
19 Johnson J W and Norton D 1991 Am. J. Sci. 291 541 DOI:10.2475/ajs.291.6.541 [Cited within:1]
20 Church C C 1995 J. Acoust. Soc. Am. 97 1510 DOI:10.1121/1.412091 [Cited within:1] [JCR: 1.646]
21 Shao W and Chen W 2013 J. Acoust. Soc. Am. 133 119 DOI:10.1121/1.4770069 [Cited within:1] [JCR: 1.646]
22 Prosperetti A 1977 J. Acoust. Soc. Am. 61 17 DOI:10.1121/1.381252 [Cited within:2] [JCR: 1.646]
23 Akhatov I, Lindau O, Topolnikov A, Mettin R, Vakhitova N and Lauterborn W 2001 Phys. Fluids 13 2805 DOI:10.1063/1.1401810 [Cited within:1] [JCR: 1.942]
24 Ferrari A 2010 Int. J. Heat Mass Transfer 53 4193 DOI:10.1016/j.ijheatmasstransfer.2010.05.042 [Cited within:1] [JCR: 2.315]
25 Ying C, An Y and Xie C 2005 J. Phys. D: Appl. Phys. 38 2489 DOI:10.1088/0022-3727/38/14/029 [Cited within:2]
26 Huang K 1963 Statistical Mechanics Cambridge Massachusetts [Cited within:1] [JCR: 1.676]
27 Yasui K 1997 Phys. Rev. E 56 6750 DOI:10.1103/PhysRevE.56.6750 [Cited within:1] [JCR: 2.313]
28 An Y and Ying C F 2005 Phys. Rev. E 71 036308 DOI:10.1103/PhysRevE.71.036308 [Cited within:2] [JCR: 2.313]
29 Flynn H G 1964 Physical Acoustics(Academic Press) [Cited within:1]
30 Gilmore F R 1950 Caltech Hydrodynamics Laboratory Report 26 4 [Cited within:1]
31 Prosperetti A and Lezzi A 1986 J. Fluid. Mech. 168 457 DOI:10.1017/S0022112086000460 [Cited within:1] [JCR: 1.415]
32 Keller J B and Miksis M 1980 J. Acoust. Soc. Am. 68 628 DOI:10.1121/1.384720 [Cited within:2] [JCR: 1.646]
33 Prosperetti A 1977 Q. Appl. Math. 34 339 [Cited within:1] [JCR: 0.728]
34 Lohse D, Brenner M P, Dupont T F, Hilgenfeldt S and Johnston B 1997 Phys. Rev. Lett. 78 1359 DOI:10.1103/PhysRevLett.78.1359 [Cited within:1] [JCR: 7.943]
35 Mansoori G A 1988 Phase Equilibrium of Mixtures Consisting of Molecules with Large Size and Sharp Differences (Thermodynamic Modeling of Supercritical Fluid Extraction and Retrograde Condensation, SFE/RC)(Gas Research Institute, Chicago, IL USA) [Cited within:1]
36 Wu C C and Roberts P H 1993 Phys. Rev. Lett. 70 3424 DOI:10.1103/PhysRevLett.70.3424 [Cited within:2] [JCR: 7.943]
37 Xu J, Chen W, Xu X, Liang Y, Huang W and Gao X 2007 Phys. Rev. E 76 026308 DOI:10.1103/PhysRevE.76.026308 [Cited within:1] [JCR: 2.313]
38 Huang W, Chen W and Cui W 2009 J. Acoust. Soc. Am. 125 3597 DOI:10.1121/1.3126943 [Cited within:1] [JCR: 1.646]
39 Crum L A 1994 J. Acoust. Soc. Am. 95 559 DOI:10.1121/1.408351 [Cited within:1] [JCR: 1.646]