†Corresponding author. E-mail: huibinwu@bit.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11272050).
The system described by the generalized Birkhoff equations is called a generalized Birkhoffian system. In this paper, the condition under which the generalized Birkhoffian system can be a gradient system is given. The stability of equilibrium of the generalized Birkhoffian system is discussed by using the properties of the gradient system. When there is a parameter in the equations, its influences on the stability and the bifurcation problem of the system are considered.
The Birkhoffian mechanics is a generalization of the Hamiltonian mechanics. Great progress has been made on its research.[1– 3] Reference [4] derived the generalized Birkhoff equations when discussing the generalized quasi-symmetric transformation of the Pfaffian action. The system whose motion is described by the generalized Birkhoff equations is called a generalized Birkhoffian system. This kind of system is a general enough constrained mechanical system. The gradient system is a kind of mathematical system with very good properties. Particularly, it is suitable for studying the problem of stability.[5] Under certain conditions, a generalized Birkhoffian system can become a gradient system. Then the stability of equilibrium and the static bifurcation of the system can be discussed by using properties of the gradient system.
The equations of the generalized Birkhoffian system have the form[6]
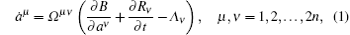
where and in the following, the same index in a term indicates to take the sum with it. In Eq. (1), B = B(t, a) is the Birkhoffian, Rμ = Rμ (t, a) are Birkhoff’ s functions, and Λ μ = Λ μ (t, a) are the added terms. We have
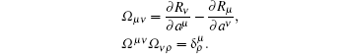
For a constant generalized Birkhoffian system, there are
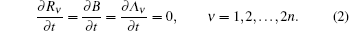
Then equation (1) becomes
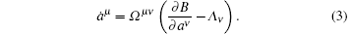
In order to discuss the equilibrium and the bifurcation problem of the system, suppose that a parameter u appears in Λ ν , namely,
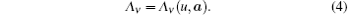
The differential equations of the gradient system have the form[5]
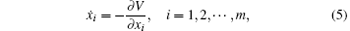
where V = V(x) is called a potential function. The gradient system has the following important properties: (i) V can be a Lyapunov function of the gradient system, and V̇ = 0 if and only if x = (x1, x2, … , xm) is an equilibrium point of the system. (ii) For the gradient system (5), the linearized system at any equilibrium point only has real characteristic roots.
The above two properties can be applied to discuss the stability of equilibrium of the generalized Birkhoffian system which has been transformed into a gradient system.
Generally speaking, the equations of a generalized Birkhoffian system cannot become a gradient system. If the following conditions:
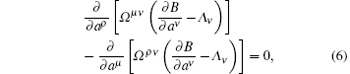

are satisfied, then the system can be transformed into a gradient system whose potential function V satisfies
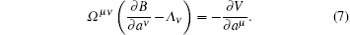
When a generalized Birkhoffian system is transformed into a gradient system, its stability of equilibrium and bifurcation problem can be studied by using the properties of the gradient system. Since the linearized system at any equilibrium point only has real characteristic roots, the stability of the zero solution can be stable, asymptotically stable, or unstable. According to Lyapunov’ s first degree approximation theory, if the roots of the first degree approximation characteristic equation are all real and negative, then the zero solution is asymptotically stable; if there is a positive real root, then it is unstable; if there is a simple zero root, and the others are not positive real roots, then it is stable, but not asymptotically stable; if there is a multiple zero root, then it is unstable.
When the added terms Λ ν have the form of expression (4), the characteristic equation will contain the parameter u. It has a great influence on the stability of equilibrium. Under certain values of the parameter, the stability of the system can take a catastrophe, namely, bifurcation.
Example 1 A generalized Birkhoffian system of the second order is

where u is a parameter. We study the relation between the stability of the zero solution and the parameter u.
The equations of the system are
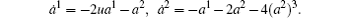
This is a gradient system whose first degree approximation equations have the following characteristic equation:
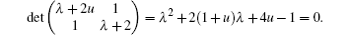
When u > 1/4, the two roots of the above equation are both negative, the equilibrium position is asymptotically stable; when u = 1/4, one root of the above equation is zero and the other is negative, the equilibrium position is stable; when u < 1/4, one root of the above equation is positive, the equilibrium position is unstable. So, when u = 1/4, the bifurcation will appear.
Example 2 A generalized Birkhoffian system is
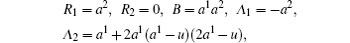
where u is a parameter. We study the stability of equilibrium of the system.
The differential equations of the system are
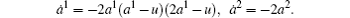
This is a gradient system. When u = 0, there is an equilibrium position (0, 0); one of the roots of the first degree approximation characteristic equation is zero, the other is negative, then the equilibrium position is stable. When u ≠ 0, there are three equilibrium positions (0, 0), (u/2, 0), and (u, 0), which are sink, saddle point, and sink, also stable, unstable, and stable respectively. So, u = 0 is a bifurcation value. When u changes from zero to non-zero, the number of equilibrium positions will increase from one to three.
The gradient system has the essential significance for studying the stability of equilibrium and the bifurcation problem. A generalized Birkhoffian system under certain conditions can be transformed into a gradient system. After that, its stability of equilibrium and bifurcation problem can be discussed by using the properties of the gradient system. The bifurcation point of example 1 shows that the equilibrium of the system changes from unstable to stable, and then to asymptotically stable. The bifurcation point of example 2 indicates that the number of equilibrium points of the system takes catastrophe. The bifurcation discussed here is not the Hopf bifurcation in the general sense.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|


