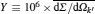†Corresponding author. E-mail: zhangqr@pku.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 10875003).
The possibility of γ-ray laser generation by the radiation of wiggling electrons in a usual background laser is discussed.
To extend the spectrum of lasers to the γ -ray range has been a dream for a long time for both nuclear and laser physicists. It means fantastic improvement of techniques, such as much more precise measurements of space-time, holography for nanometer size or even smaller objects, and so on. There are various proposals[1– 7] for its realization, including those of using nuclear decay and condensed positronium decay, and those of using γ -ray emitted by wiggling charged particles. References [1] and [2] are review articles. We preferred the way of using the radiations from charged particles wiggling in a periodically bent crystal.[5– 7] However, this proposal assumes that the crystal is ideal. Contrarily, the real crystals are not ideal. They have lacunae and impurities. This point affects the reliability of the proposal. Another problem is that the theory used in this proposal is not fundamental, which also spoils its reliability. Moreover, to bend the crystal periodically in small space– time is not easy. Here we propose a way for the γ -ray laser generation, which keeps the basic ideals of this proposal, but without its shortcomings.
Physically a laser is a classical limit of an electromagnetic wave, simple and clean. It wiggles charged particles in a well-known way, therefore is an ideal wiggler for further laser generation, including those in the γ -ray range. The whole process may be described by a fundamental theory, quantum electrodynamics, which is the best theory in physics nowadays. We therefore reformed the quantum electrodynamics[8] for this purpose, to see whether it may offer a better way for the γ -ray laser generation or not. The main change is to substitute the laser state for the usual vacuum state; the latter was defined to be a state without any photon and charged particle. The quantization of the electromagnetic field is now around a given laser state instead of the usual vacuum state. Base wave functions for the electron field quantization are changed to the solutions of the Dirac equation for an electron in the given laser, instead of that in the usual vacuum. These new base wave functions are periodically distorted, showing the quantum wiggling of electrons in the laser. This is a new picture of quantum electrodynamics, equivalent to its other pictures. As in the original picture, the Hamiltonian of the system is also divided into two parts. One is for the free motion, another is the interaction between the free parts. Now, however, the electrons are wiggling under the action of the applied laser. Their freedom only means that they do not emit or absorb photons. Photons now are quanta of the fluctuation of the electromagnetic field relative to the given laser. The laser, a given classical part of the electromagnetic field is subtracted. This free Hamiltonian is exactly handled like that in the original picture. Interaction Hamiltonian governs the emission and absorption of a single photon by an electron. It is handled by perturbation. This is safe because of the smallness of the fine structure constant α . We see that the proposal is on a sound foundation. It is as sound as the usual form of the quantum electrodynamics.
On this foundation we find that, in a head-on collision between a mono-energy electron beam and a laser, in a wide range of electron energy and laser frequency, a beam of γ -ray appears on the forward direction of the electron motion. It is almost completely polarized, mono-directional and monochromatic. It is therefore worth trying the γ -ray laser generation in this way.
There has been a lot of work on electron laser collisions, both theoretical and experimental.[9– 17] Theoretical works are based on the Compton formula and Klein– Nishina formula for the Compton scattering, [18– 21] which are derived from the quantum electrodynamics in a vacuum, [22, 23] but without considering the stimulated emission of electrons. The coherence of photon states in the laser[24– 30] is also overlooked. Experimental works found a way for generating intense γ -ray by the Compton backscattering (CBS). However, overlooking stimulated emissions, they overlooked the possibility of making a γ -ray laser in this way. We hope these imperfections may be remedied.
In Section 2, we explain how a laser wiggles electrons and makes them emit γ -quanta. The physics is emphasized. Nevertheless, it is as quantitative as that given by the systematically quantum electrodynamical derivation done in Ref. [8] Formulae for the following calculations are given. In Section 3, we show numerical results obtained by these formulae, explaining why we can generate γ -ray lasers in this way. Section 4 describes the evolution of the γ -ray intensity, because of the balance between the γ -quanta emission and reabsorption, a possible intensity limit is discussed. Section 5 proposes further amplification of γ -ray laser. Section 6 confirms the coherence of the generated γ -ray laser. Section 7 is the conclusion.
A laser is a classical limit of an intense electromagnetic wave and is well described by a classical 4-potential. In the Coulomb gauge, a circularly polarized laser is described by the vector potential
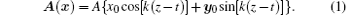
It is a plane wave circularly polarized in the x– y plane and propagating along the z direction, with a wave vector k = kz0 and an amplitude A. x0, y0, and z0 are unit vectors along x, y, and z directions respectively. The Dirac equation for an electron in this laser is
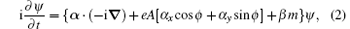
with ϕ ≡ k(z – t). e is the absolute value of the electron charge, and m is the electron mass. Dirac matrices defined in Lurie’ s book[22] and the nature unit system (c = ћ = 1) are used. The operator on the right hand side of this equation is time dependent. Fortunately, a time dependent unitary transformation generated by the operator e− iktjz removes this time dependence, [27] in which

is the z-component of the angular momentum of the electron. φ is the azimuth angle of the electron, defined to be the angle between the projection of the electron radius vector on the x– y plane and the x-axis. Σ z is the z-component of the Pauli matrices. The transformation

is a rotation around the z axis with angular velocity k. The resulting picture is therefore called the rotation picture, and denoted by the subscript r. Multiplying e− iktjz on two sides of equation (2) from the left, we obtain the wave equation
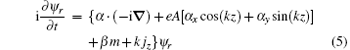
in the rotation picture. The operator on the right hand side of this equation is no longer time dependent. We therefore have stationary solutions ψ r(x, t) = U(x)e− iε t for this equation. They satisfy the eigen-equation
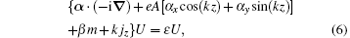
in which U(x) is an eigenfunction and ε is the corresponding eigenvalue. This equation is exactly solved, [8, 31] with

and
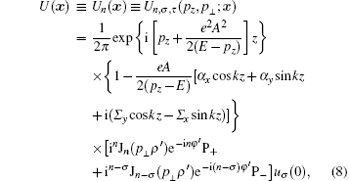
where p, 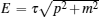
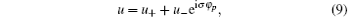
with
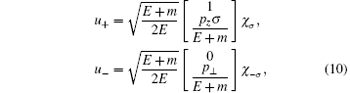
in which χ σ is an eigenspinor of Σ z with eigenvalue σ . For given pz and p⊥ , the bispinor (9) is characterized by σ and φ p, therefore may be denoted by uσ (φ p). The bispinor uσ (0) at the end of Eq. (8) is defined in this way. The projection operator P± ≡ (1± σ Σ z)/2 gives P± uσ (0) = u± . (ρ ′ , φ ′ , z) in wave function (8) are coordinates of the electron position, in which (ρ ′ , φ ′ ) are defined by

These equations constitute a z-dependent linear coordinate transformation from Cartesian coordinates (x, y, z) to (x′ , y′ , z) in the x– y plane, followed by a transformation from rectangular coordinates (x′ , y′ ) to polar coordinates (ρ ′ , φ ′ ) in this plane. The factor 1/2π on the right hand side of solution (8) is a normalization constant. The set [Un, σ , τ (pz, p⊥ ; x)] of all eigenfunctions is therefore orthonormal, so that

Since in this work we are interested only in the electron-laser interaction, always have τ = 1, the eigenfunctions will be simply denoted by Un(x) ≡ Un, σ (pz, p⊥ ; x) ≡ Un, σ , 1(pz, p⊥ ; x) in the following.
At the limit A → 0,
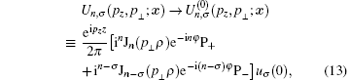
where ρ , φ , and z are cylindric coordinates of the electron. The right hand side is a solution of the Dirac equation for a free electron, and

is a plane wave solution of the Dirac equation for a free electron of momentum p = p⊥ (cos φ px0 + sin φ py0)+ pzz0, u is defined by Eq. (9). In the case of p⊥ = 0, we have

It is nonzero only when n = 0. In this case, it is already a plane wave of an electron with momentum p = pzz0. Now we see the influence of the laser on the electron motion. It is the distortions of the electron wave in the x– y planes, periodically along the z direction, and the modulation of the periodicity along the z direction. It is the wiggling of electrons. Since it appears in the wave function instead of in their trajectories, we call it quantum wiggling.
The wiggling electron radiates because of the interaction eα · A′ between the electron and the electromagnetic field fluctuation around the laser. A′ is the difference between the total electromagnetic vector potential and the vector potential (1) of the laser. It is decomposed into various modes, each with a wave vector k′ and a polarization vector e′ , perpendicular with each other in the Coulomb gauge, and denoted by ι ′ ≡ (k′ , e′ ). It is quantized. In the interaction picture, the wave function associated with a photon of mode ι ′ is[22]

In the rotation and interaction picture, the interaction matrix element for the electron transition from the state Un, σ (pz, 0; x) to the state Un′ , σ ′ (p′ z, p′ ⊥ ; x) and emitting a photon of wave vector k′ and polarization e′ is

in which
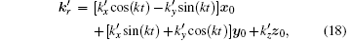
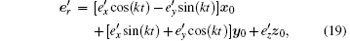
are k′ and e′ respectively in the rotation picture. They rotate around the z axis with an angular velocity k. The rotation transformation makes the unperturbed Hamiltonian of an electron in the background laser time independent, and makes the perturbation of the electromagnetic field fluctuation on the electron periodically time dependent. These two changes working together result in the equivalence of the rotation picture with the original one, and makes the problem able to be handled by the usual time dependent perturbation.
Take 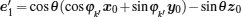
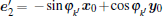
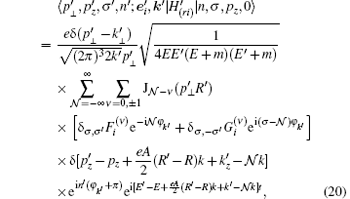
with
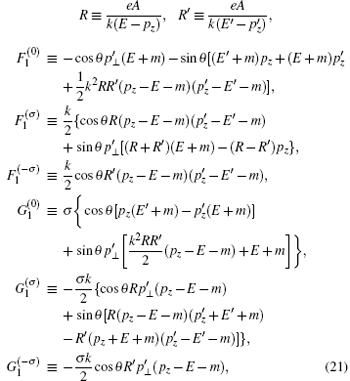
and

where 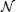
Suppose a free electron of momentum p = pzz0 and spin σ /2 comes from the remote past and meets a laser on the way. It evolves according to the Gell– Mann Low theorem[32] into the state Un, σ (pz, 0; x). The above analysis shows that this state may transit to a superposition
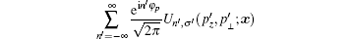
of electron states in the laser due to the electromagnetic interaction 
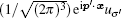
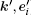
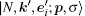
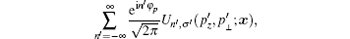
and the number of the photon in mode (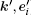
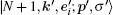
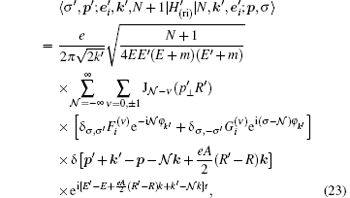
in which the factor 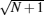
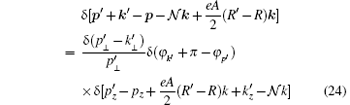
is a three-dimensional δ -function.
In the first-order perturbation, the transition amplitude of the process is

where δ -functions give selection rules for non-zero transition probability. They are
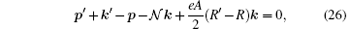

In the limit A = 0, they like the usual momentum and energy conservation of the process, if 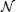
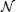

For the given collinear incident electrons and background laser, this formula gives the direction dependence of the emitted photon energy. In the case of 
of the corresponding Compton scattering.[18, 19]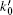
The transition probability per-unit time in the unit volume and unit solid angle of k′ is[8]
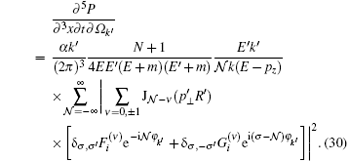
In our unit system, the Compton wavelength of an electron is m− 1. In the unit of m− 2, the differential cross section of a piece of laser of volume m− 3, in which a photon of momentum k′ and polarization 

For an arbitrarily given polarization 
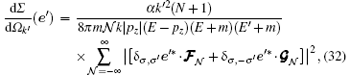
in which
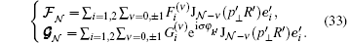
For definite σ , σ ′ , and 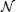


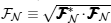
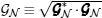
Consider the head on collision between an electron beam and a circularly polarized laser. To be definite, we take the titanium sapphire laser of wave length 660 nm to 1180 nm tunable. From the middle, we set the wave length of the laser to be 785 nm. This kind of facility may be found in many laboratories over the world. By compression, the pulse intensity of this kind of laser may be as high as 2× 1026 W/m2.[33] However, the theory derived above is valid only when the applied laser may be considered as a plane wave. The linear dimensions of the laser pulse have to be much larger than the wave length. It means that the laser should not be over compressed. We would take a moderate intensity. It is 1019 W/m2. The energy of the incident electrons is limited in the range 102 to 103 MeV. It may be found in many laboratories too.
Now, a circularly polarized plane wave laser of wave length 785 nm propagates along the z direction. A beam of electrons, each with energy E, moves towards the – z direction. Electrons wiggle in the laser and emit photons. Equations (30) and (31) show that the emission probability decreases rapidly with the increase of the integer 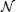
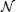
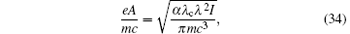
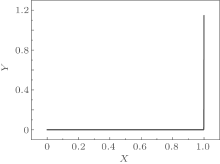
in which λ is the wavelength and I is the intensity of the laser. λ c = ћ /mc = 0.386 pm is the Compton wavelength of the electron. Fixing I = 1019 W/m2 and λ = 785 nm, we get A = 1.5× 10− 2mc/e. Figure 1 shows the calculated relation between the energy of the emitted photon on the forward direction of the incident electron motion and the energy of the incident electron. We see that the energy of the emitted photons are in the γ -ray range.
For an unpolarized incident electron beam, if the spin states of the outgoing particles are not measured, the probability of finding a photon emitted in direction of k′ is proportional to the average differential cross section
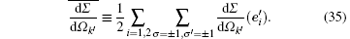
Substituting parameters
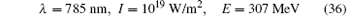
into Eqs. (31) and (35), we obtain numerical results for the average differential cross section as a function of θ , which is shown in the Fig. 2. The angular distribution for the γ -photon emission is very characteristic. Photons concentrate in the forward direction of the incident electrons, and form a very sharp peak on this direction. It means an almost mono-directional emission. The single valued relation (28) between the energy and the direction of the emitted photon tells us, it also means an almost monochromatic emission. The stimulated emission makes positive feedback, and therefore makes a collapse of the distribution into an almost geometric line with very high intensity. This is the γ -ray amplification by stimulated emission of radiation. Using Eqs. (21) and (22), we find, from the description at the end of the last section, that the polarization vector of the forward radiation emitted by electrons is certainly
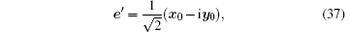
independent of the spin states of the incident electrons. The radiation emitted by wiggling electrons is therefore completely polarized. A radiation, even though mono-directional, monochromatic and completely polarized, does not necessarily mean a laser. A laser must have a nonzero coherence amplitude, like the amplitude A of the laser (1). It requires that the photon number of the state is not certain. Theoretically, this is not a problem in our case. The stimulated emission makes the photon number in the final electromagnetic state uncertain. The radiation emitted by wiggling electrons should therefore be a γ -ray laser, to be confirmed by experiments.
On the other hand, the coherence amplitude A = 1.5× 10− 2mc/e in our case here is small. We have seen, in this limit, the energy of the photon emitted by wiggling electrons in a laser with 
Suppose electron-laser collisions happen in a tube of cross section S and length L, with 

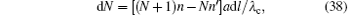
in which 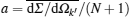
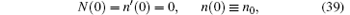
we have

Substituting them into Eq. (38), we obtain
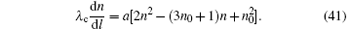
This is the evolution equation of the process. The solution n(l) under the initial conditions (39) and, by Eq. (40), also N(l) and n′ (l) are obtained

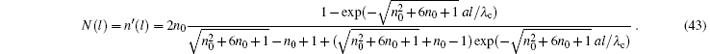
Take parameters (36), which have been used in making Fig. 2, we obtain λ c/a = 337 nm. For tube length L = 1 cm, aL/λ c is already practically infinity. Equation (43) shows, in this case, at end 2 of the tube, the number density of γ -quanta in the generated γ -ray laser approaches a constant, which is about a half of the number density of the incident electrons. This is a result of the balance between emissions and absorptions of γ -quanta by the initial state and final state electrons respectively in the tube. The intensity of the output γ -ray laser is therefore almost determined by the intensity of the input electron current. For an electron beam of density n0 = 1018 m− 3 and energy E = 307 MeV, which may be found in many laboratories, the intensity of the output γ -ray laser is about 5× 1013 W/m2. It is meaningful.
To generate a more intense γ -ray laser by the head on collision between an electron beam and the usual laser, one needs a more intense electron beam. This situation is somewhat similar to the generation of the usual laser by the coherent decay of a dense aggregate of similarly excited atoms, without pumping. The intensity of the laser is therefore limited by the limit density of the laser generating medium. In our case, it is limited by the density of the electron beam. In the theory presented above, Coulomb interaction between electrons is totally omitted. This is not permissible if the density of the electron beam becomes too high. Denote the mean linear dimension occupied by an electron in the beam by r. The Coulomb force between two neighboring electrons is α /r2 in nature units. On the other hand, the electric force of an applied laser acting on an electron is eAk, in which A and k are the amplitude and the circular frequency of the laser respectively. Therefore, the Coulomb interaction is omissible only when 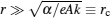
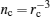
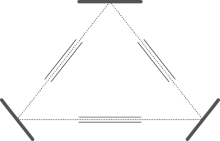
The space charge problem may also be solved in a technical way. It is to divide one high density electron beam into many sub-beams with much lower densities, and inject them into the active tube from different entrances at different times. Entrances are opened on the wall of the tube, distributed along its length direction. The electron sub-beams are injected through them by suitably designed magnets so that the injected electrons move along the central axis of the tube. The injection time is also controlled to let the injected electrons meet the already emitted γ -quanta as soon as they arrive at the central axis, so that the stimulated emissions may continue. Figure 3 is a sketch map of the designation. We also open exits for electrons, one by one with the entrances, on the wall of the tube. After participating in the emission and absorption of γ -quanta, electrons are removed from these exits by suitably designed magnets, just before new electrons being injected through the corresponding entrances.
 | Fig. 3. Sketch map for the multi-section active tube. The space between two parallel black lines shows the inside of the tube, while dotted lines show the trajectories of the electron injection. |
The active tube is now constituted by its sections, each begins from an entrance and ends at an exit. The tube analyzed above is a single section one. We may analyze each section in a multi-section tube in a similar way. Let us concentrate on one section of the tube. l denotes the distance between a point in the section and the entrance of this section. Start from Eq. (38). We need a modification for the initial conditions (39). The γ -quantum number density at the beginning of a section is N(0) ≡ N0 ≥ 0 in general, the equal mark works only for the beginning section. Equation (40) now is substituted by N(l) = N0 + n′ (l) = N0 + n0 − n(l). The evolution equation is generalized to be
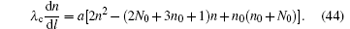
This is slightly more complicated than Eq. (41), but is still analytically solvable. An analysis similar to that made in the Section 4 shows, for the case with parameters (36), in a section of length L ∼ centimeters, after a balance between emissions and absorptions, the net increase of the average photon number density of the γ -ray laser at the end of the section, is still a noticeable fraction of the number density n0 of newly injected electrons.
At the beginning of the new section, the initial state electron number density restores its original value n0, and the final state electrons are removed. It is similar to the pumping in the usual laser generation. The intensity of the laser is therefore multiplied by this mechanism. A κ section tube makes κ times pumping, and therefore intensifies the γ -ray laser, roughly say, by a factor of κ . For the applied laser with parameters (36), the section length is of the order of centimeters, and the length of a 100 section tube is of the order of meters, which is acceptable. For the incident electron beam of density n0 = 1018 m− 3, the intensity of the final output γ -ray laser is of the order of 1015 W/m2. If the density of the incident electron beam becomes n0 = 1023 m− 3, we will have a γ -ray laser of intensity 1020 W/m2.
The intensity of a multi-section γ -ray laser is also influenced by the intensity of the applied laser. A more intense incident laser gives a larger emission probability for an electron wiggling in it, which in turn gives larger coefficient a in the evolution equation (44) and shorter section in the active tube. An active tube of given length may therefore contain more sections and give higher intensity for the γ -ray laser.
A long (several meters or several ten meters), thin and well collimated many sectioned active tube also plays a role here, which was played by a resonator in the usual laser generation. It selects a definite mode of γ -radiation, with definite direction, therefore definite wavelength and definite polarization, to amplify by stimulated emissions. Other modes are washed out from the amplification, because of the positive feedback. A longer and thinner active tube makes the quality of the γ -ray laser better. We call this structure a linear intensifier of the γ -radiation.
One may change the direction of a soft γ -radiation by Bragg-reflection, and therefore may arrange the sections of the active tube for amplifying this radiation in a cyclic way. In principle, this structure may make a huge number of amplifications for the γ -ray by stimulated emissions in a finite space, and reach a very high intensity, if the reflection efficiency is high enough. We call this structure a cyclic intensifier of the γ -radiation. A sketch map of it is shown in Fig. 4. Unfortunately, the Bragg-reflection works only for soft γ -radiations with wavelengths of the order of the lattice constants of some crystals, it is of the order of Angstroms. Only lasers composed of soft γ -photons may be intensified in this way. For example, in the head-on collision between a usual laser and a beam of electrons with parameters
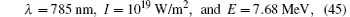
the energy of the output photon on the forward direction of incident electrons is 1.424 KeV, which is in the soft γ -ray range. We expect the γ -ray of this kind may be intensified by the cyclic intensifier to a rather high intensity.
Finally, we have to confirm that the generated and amplified γ -ray is indeed a laser. The most direct way for this purpose is to measure its coherence amplitude A, and to see whether it is nonzero or not. Equation (28) of 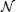
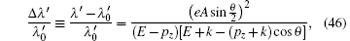
where λ ′ ≡ 2π /k′ and 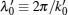
Suppose that the output soft γ -radiation generated in the electron-laser head on collision with parameters (45) is intensified to a high intensity of I = 1026 W/m2 by a cyclic intensifier. A beam of electrons of energy E = 5.135 MeV is injected into the radiation along its propagation direction. Electrons interact with the radiation and emit ultraviolet radiation on the direction against the γ -ray propagation. Equations (28), (34), and (46) show that, if the γ -radiation is completely coherent, the wavelength of the emitted ultraviolet radiation would be λ ′ = 351 nm, and the wavelength shift due to the nonzero coherence amplitude A would be 2.77× 10− 3. They may be detected and checked by experiments, using normal optic techniques, well developed about a century ago, for the fine structure research in the atomic spectroscopy.
It is possible that the γ -ray is constituted by parts. One forms a coherent state, it is the laser. Another is a non-coherent aggregate of photons. The variable I in the equation (34) is the intensity of the coherent part. To be definite, we call it the coherent intensity. Combining equations (34) and (46), we see

in the nature unit system. The wavelength shift is proportional to the coherent intensity of the radiation. In the above example, we assumed that the radiation intensity equals its coherent intensity. The radiation, as a whole, is a laser. If there are non-coherent photons, the coherent intensity will be lower than the total intensity. It results in a smaller wavelength shift. In other words, smaller wavelength shift means incomplete coherence. If in the above example a smaller wavelength shift, say Δ λ ′ /λ ′ 0 = 2.77× 10− 4 is observed, one has to conclude that only one tenth of emitted photons form a coherent state. Other photons are non-coherent.
Based on quantum electrodynamics, we have shown that, both in the head on electron-laser collision and in the Compton backscattering, the emitted photons may form a γ -ray laser. The competition and balance between the emission and reabsorption of γ -quanta by electrons determine the evolution and therefore the output intensity of the γ -ray laser.
In electron– laser collisions, incident electrons, wiggled by the applied laser, emit γ -photons. The stimulated emissions amplify the γ -radiation and form the γ -ray laser. In this sense, the generated γ -ray laser is a free electron laser (FEL). The new aspect here is that the electron motion in the background laser is governed and exactly solved by quantum mechanics. Therefore, it is a quantized free electron laser (QFEL). This mechanism may be understood in a usual way as well. The incident electrons are higher state systems in the background laser. They transit into final (lower) state and emit γ -photons. The stimulated emissions again make the γ -ray laser. Two understandings of the γ -ray laser generation are unified in quantum theory. In this way, ideas in the usual laser theory, such as pumping, resonator, positive feedback, and so on are usable in the analysis. By use of them, we propose some ways to intensify and qualify γ -ray lasers. Analytical and numerical estimations show that the possible generated γ -ray laser may be intense enough to be detected and researched. A way for measuring the coherence amplitude A, and therefore confirming the coherence of the γ -ray laser is proposed.
Of course, it is not easy to work out these proposals. Many technical problems have to be solved before their realization. For example, the theory is developed under an ideal condition, in which incident electrons have identical energies and move on identical directions, and the background laser is a plane wave. In reality, one can infinitely approach this condition, but cannot reach it. The experience of the usual laser generation tells us, there is a critical bound around the ideal condition. Crossing over the bound makes the positive feedback of the stimulated emission become dominating, and the emitted photons collapse into a laser. This is a phase transition. To find the critical bound and realize the phase transition for a γ -ray laser would be a great deal of work, mainly experimental.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|