Fractal geometry theory plays an important role in the nonlinear field.^{[1– 9]} The diffusion limited aggregation (DLA) model proposed by Witten and Sander, which explains the far-from equilibrium natural phenomenon, is an especially hot research topic.^{[10– 13]} Various improved DLA models have been proposed to better explain specific growth processes such as dendritic growth, ^[14] electro-deposition, ^[15] and fluid displacement.^[16] The DLA model allows researchers to obtain the features of fractal growth and derive the morphology control theory under some two-dimensional growth conditions.^{[17– 19]} However, natural fractal growth is conducted in the three-dimensional space and the actual system is usually expected to control the fractal growth form in a fixed region, such as crystal growth occurring along specified axes, non-uniform bacterial colony growth, and particles aggregating along a certain orientation. At present, the orientation restriction issue for fractal growth is usually addressed only in experimental research, ^{[20– 22]} and it is seldom tackled theoretically. Meanwhile, many external environmental factors may interfere with the process of fractal growth, which makes it complicated and difficult to predict the morphology of fractal growth. Therefore, the research on the directed prediction and control of three-dimensional fractal growth is of great significance.

We consider a space body in a real environment and provide a directional region control model for the thermal fractal diffusion system. The quantitative relationship between the particle aggregation probability and the interference term is obtained using the norm theory, in which the nonlinear interference term and the internal heat source term are generalized functions. Under certain conditions, the source term can suppress the nonlinear interference term, meaning that the source term controls the growth particles to aggregate in a different direction or region. This situation is called directional region control (DRC) in this paper. We predict the aggregation morphology of particles in differently directed regions, and achieve the DRC of space body thermal diffusion growth.

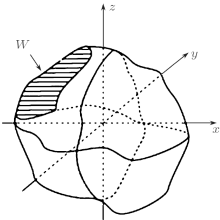
Considering the thermal diffusion of a space body W (as shown in Fig.  1) in an actual complex environment, we take the thermal diffusion process as a distributed parameter system meeting the boundary conditions, ^[23]

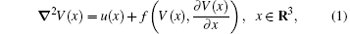
where V(x) refers to the space body W ’ s temperature (the probability of thermal diffusion) at certain point x, and u(x) refers to the density of the inner heat resource. The f is a nonlinear function, referred to as the forced term in physics; u(x) is a quantitative initial condition, referred to as the source term. By assuming G = u(x) + f (V(x), ∂ V(x)/∂ x), both the nonlinear interference term f (V(x), ∂ V(x)/∂ x) and the source term u(x) can be regarded as a part of the environmental interference term G, which is assumed to be an arbitrary function. Figure  2 shows the thermal fractal diffusion aggregation cluster without environmental interference.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. A space body W.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The thermal diffusion of the space body W (f = 0, u = 0).

Generalized functions can be regarded as continuous linear functionals of function space and are applied extensively in mathematics, physics, mechanics, and engineering.^[24] Let us assume that both f (V(x), ∂ V(x)/∂ x) and u(x) are generalized functions, and that these generalized functions are all elements in a basic function space K. In general, it is very difficult to find an analytical solution to the nonlinear partial differential equation (1). By studying the weak solution to system (1), we discuss the quantitative relationship between the particle aggregation probability and the environmental interference term G.

Definition 1 (L² space) Assume that Ω is a bounded domain of R³. We use L²(Ω ) to express the function class consisting of all the measurable functions V(x) which are defined in Ω and meet ∫ _Ω | V(x)| ² dx < ∞ . The L²(Ω ) is a vector space with norms defined as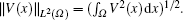

Definition 2 (Sobolev space H^k) Assume that Ω is a bounded domain of R³. We use H^k(Ω ) to express the function class consisting of all the measurable functions which are defined in Ω and meet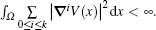 The H^k(Ω ) is a vector space with norms defined as

Definition 3 Assume that a(V, v) is a bilinear functional in Hilbert space H, i.e., V and v are both linear.

(i) a(V, v) is bounded, if there is a positive constant M ≥ 0, such that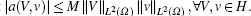

(ii)| a(V, v)| is compulsory, if there is a positive constant δ > 0, such that

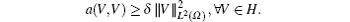
Now we can consider the existence and uniqueness of the weak solution of the following system:

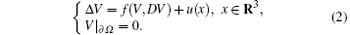
Theorem 1 Assume that u(x) ∈ L²(Ω ), f (V, DV) ∈ L²(Ω ). There exists a unique weak solution to system (2), and the following estimation exists:

where λ is a positive constant.

Proof Denote

Obviously, a(V, ψ ) is bilinear. First, we prove the boundedness of a(V, ψ ),

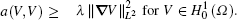
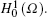
Next, due to the ellipticity condition, we have So a(V, ψ ) is compulsory. Let us prove that F(ψ ) = ∫ _Ω uψ dx is a bounded functional in . The F(ψ ) is linear. According to the Hö lder inequality, we have

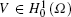
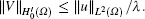
Therefore, according to the Lax– Milgram Theorem, ^[25] there exists a unique such that . Thus, is the only weak solution to system  (2).

To improve the regularity of the weak solution for system  (2), we introduce the difference operator. If V(x) is a function defined on R³, then where e_i is the unit vector in the direction of x_i and is the difference operator along the direction of x_i . Next, we introduce some of the basic properties of the difference operator.

Proposition 1 We have the following basic properties of the difference operator.

(i) The adjoint operator of for any integral functions, f (x), g(x) ∈ L²(Ω ), there is an integral equation

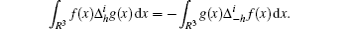
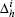
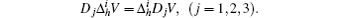
(ii) The differential operator and are exchangeable; for any weak differentiable function ϕ

(iii) The difference of products can be expressed as

where T_i is the shift operator in the direction of

Proposition 2 Assume that Ω ⊂ R³ is a region.

(i) Assume that V ⊂ H¹(Ω ), Ω ₁ ⊂ ⊂ Ω . For| h| > 0, when sufficiently small, 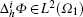, giving the following estimation formula

(ii) Assume that V ⊂ L²(Ω ) and there exists a constant K such that Ω ₁ ⊂ ⊂ Ω . When| h| > 0 is small enough, where K is unrelated to h. Then giving the following estimation formula

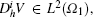
We can obtain Theorem 2 using the basic properties of the difference operator.

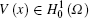
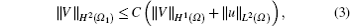
Theorem 2 If ) is the weak solution of system (2) and Ω ₁ ⊂ ⊂ Ω , then V ∈ H² (Ω ₁) and we have

where C is a positive constant that only depends on the distance dist {Ω ₁, ∂ Ω } from Ω ₁ to ∂ Ω .

Proof Supposing Ω ₁ ⊂ Ω , we note that d = dist {Ω ₁, ∂ Ω }/4. The cut-off function dist{suppη , ∂ Ω } ≥ 2d.

Based on the definition of the weak solution and the density of in we conclude that

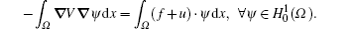
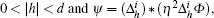
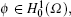
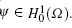
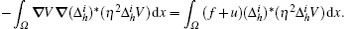
If h meets the condition then dist{suppψ , ∂ Ω } ≥ d, and therefore, Substituting ψ into the above integral equation, we can obtain the following formula:

By applying the exchangeability of the difference operator and the differential operator, and the relationship between the difference operator and its adjoint operator, the above integral relationship can be rewritten as

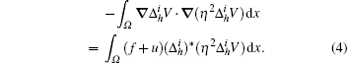
The following formula is obtained from formula (4) by calculation:

For further calculations, we need to estimate the third term on the right side of formula  (5). From Proposition 1, we conclude that

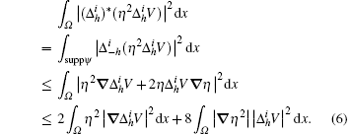
Substituting formula (6) into formula (5), we obtain

and then

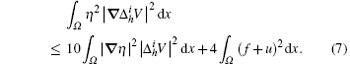
Next, if we estimate the first term in formula (7) by using the cut-off function and Proposition 1, then we have

Substituting formula (8) into formula (7), we conclude that

Based on the above formula and using the cut-off function, we have

Based on Proposition 2, we can conclude that formula (3) is correct. The proof is completed.

Based on Theorem 1, we can conclude that when f (V(x, y, z), DV(x, y, z) ∈ L²(Ω ), u(x, y, z) ∈ L²(Ω ), and 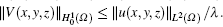The source term u(x) can restrain the nonlinear influence of the generalized function term f (V(x), ∂ V(x)/∂ x) on the thermal fractal diffusion. This allows the thermal particle to be aggregated in different directions or regions, and achieves directed control.

By assuming that u(x) is a constant k, f(V(x), ∂ V(x)/∂ x) = a sin²(V(x)), and f(V(x), ∂ V(x)/∂ x) = bV(x)² + c sin(V(x)), the control region H of the source item u(x) can be taken as a one-eighth space, one half space, cuboid region, spherical domain, or sectional region.

The thermal diffusion of a space body is a random process induced by a temperature gradient. In our recent work, ^[23] the thermal diffusion fractal growth was simulated. The growth-probability function of every possible aggregation point has a nonlinear relationship with the temperature gradient. With the environmental disturbance, the boundary condition V(x) is set to be zero at any point on the aggregation surface, and for the boundary at infinity, V(x) is set to be one, which provides a stable particle flow. By modifying the movement-boundary conditions of the mathematical model, the temperature gradient can be calculated from the Poisson equation. Furthermore, by using the roulette wheel selection algorithm, the particle aggregation location can be determined.

With the environmental interference considered, the thermal diffusions in different regions are simulated by using the simulation method in the literature.^[23] As shown in Figs.  2– 5, the interference source item controls the aggregation of the thermal particles in different directions. This result shows that our control method is valid.

A fractal dimension is an index for characterizing fractal patterns or sets by quantifying their complexity as a ratio of the change in detail to the change in scale. It has also been considered as a measure of the space-filling capacity of a pattern, which tells how a fractal scales differently from the space it is embedded in.^[26] As the thermal diffusion system of a space point source has an obvious central point, the Sandbox method is used to calculate the fractal dimension (D_f) of the thermal aggregation cluster with different interference actions.^[27] Figure 6 shows the comparison between the thermal diffusion fractal dimensions of different sectional control regions. Figure  5 shows the results predicted by our DRC model for spherical domain, where the spherical interference control region is

and the sectional control region is

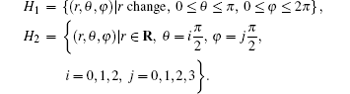
According to Fig.  6, the aggregations of thermal particles based on the spherical control region are more complex than that controlled in different directions in addition to the spherical domain. Although they share the same control spherical domain, the directed region control beyond spherical domain determines the growth direction and also reduces the growth complexity. Figure  6 also shows that the fractal dimensions of clusters aggregated in the multidirectional region are larger than those of clusters aggregated in the unidirectional region for the same spherical domain. This indicates that the complexity of thermal aggregation clusters increases along with the increase in multidirectional control.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Thermal fractal diffusion in different interference space regions: (a) 0 ≤ θ ≤ π /2, 0 ≤ φ ≤ π /2, (b) π /2 ≤ θ ≤ π , π ≤ φ ≤ 3π /2, (c) π /2 ≤ θ ≤ π , 3π /2 ≤ φ ≤ 2π , (d) 0 ≤ θ ≤ π /2, 0 ≤ φ ≤ π .

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Thermal fractal diffusion under control conditions in differently directed regions: (a) θ = π /2, φ = jπ /2, j = 0, 2, (b) θ = π ; θ = π /2, φ = π , (c) θ = iπ /2, i = 0, 2; θ = π /2, φ = jπ /2, j= 1, 3, (d) θ = iπ /2, i = 0, 2; θ = π /2, φ = jπ /2, j = 0, 1, 2, 3.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Thermal fractal diffusion with variation of the spherical domain and sectional region: (a) r ≤ 8; θ = 0, (b) r ≤ 8; θ = π ; θ = π /2, φ = jπ /2, j = 2, 3, (c) r ≤ 9; θ = π /2, φ = 3π /2, (d) r ≤ 10; θ = π /2, φ = jπ /2, j = 2, 3, (e) r ≤ 11; θ = π /2, φ = jπ /2, j = 0, 1, 2, 3, (f) r ≤ 14; θ = iπ /2, i = 0, 2; θ = π /2, φ = jπ /2, j = 0, 1, 2, 3.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. The fractal dimensions for the thermal diffusion clusters in Fig.  5 under variant spherical domain controls, and those under variant sectional controls.

We have presented a DRC model of thermal fractal diffusion with actual environmental interference. Based on the norm theory, the control analysis of this model is given. When the nonlinear interference terms and the inner heat source terms are generalized functions, the quantitative relationship between the particle aggregation probability and the disturbance term can be obtained using the norm theory. Our simulations show that this DRC model for the thermal diffusion fractal growth of a space body is valid. This paper addresses only the generalized form of the disturbance term in L² space. If the generalized function belongs to the space L^p(p ≥ 1), then the DRC of space fractal growth will be of universal significance. The more complex theoretical structure will be subject to greater change and we will address the topic in a separate paper.