Understanding many-body physics in one dimension from the Lieb–Liniger model*
Jiang Yu-Zhua),b), Chen Yang-Yanga),b), Guan Xi-Wena),b)†
       
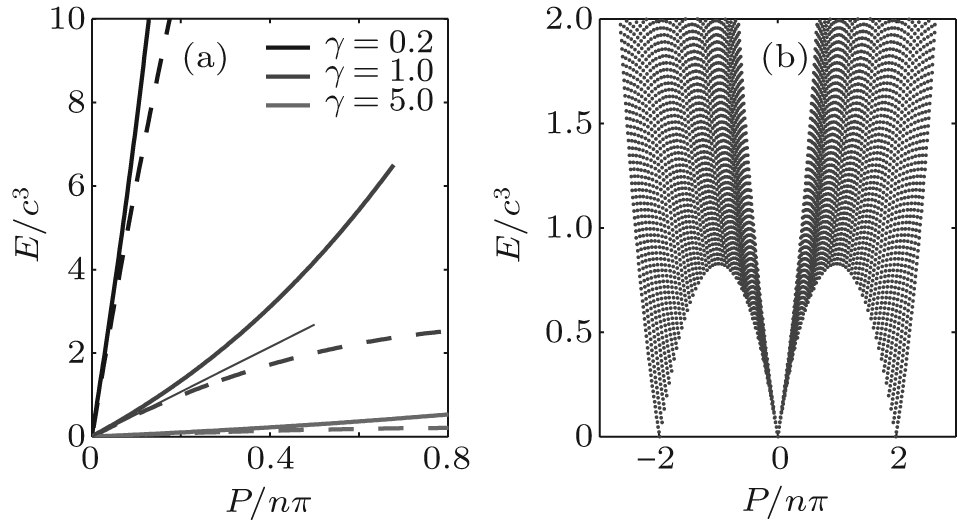
Dispersion relations in elementary excitations: adding one particle and adding one hole excitation. (a) Solid lines: the spectra for adding one particle to the ground state corresponding to the configuration presented in Fig. 3(b) . Dashed lines: the dispersion relations for the hole excitation, see the configuration shown in Fig. 3(c) . For γ = 1, the thin blue line is calculated by using Eq. ( 44 ). We see that both the particle and hole excitations comprise the dispersion relations with the same velocity. (b) The particle–hole excitation spectra, see Fig. 3(d) . The linear dispersion relation is seen for the long-wavelength limit, i.e., the momentum tends to be zero.