Investigation on quantum phases in lattice systems with fermions or bosons and transitions between these phases is a significant topic in condensed mater physics due to its potential promises in application and theoretical research. Novel quantum phases including topological (Mott) insulators, quantum (spin) Hall effects, and superconductivity and transitions between these states have been found and studied extensively in typical lattices, such as the honeycomb lattice, square lattice, triangular lattice, and square-octagon lattice.^{[1– 14]}

The square-octagon lattice with fermions has been studied by different groups and many splendid results have been achieved, such as the achievement of topological insulator through considering spin– orbit coupling and the comprehensive discussion on quantum magnetic phase transitions in the square-octagon lattice with fermions.^{[15– 17]} Herein the effects of interaction, temperature, and anisotropic parameter on the quantum phase transitions of anisotropic square-octagon lattice with fermions are studied through combining the cellular dynamical mean field theory^{[18– 21]} with continuous time quantum Monte Carlo algorithm^[22] under the framework of the single band Hubbard model.^{[23, 24]}

The remainder of this paper is organized as follows. In Section 2, the sketch map of a square-octagon lattice with fermions and the model and methods used to describe this lattice system are introduced in detail. In Section 3, the effect of interaction and temperature on the quantum phase transition in an anisotropic square-octagon lattice with fermions for a fixed anisotropic parameter, and the relation between interaction and anisotropic parameter for fixed temperature are shown based on the calculations of the local single particle density of states and double occupancy. A brief discussion and conclusion are given in the last section.

The square-octagon lattice is a bipartite lattice that can be thought of as a square lattice in which each vertex has been decorated with a tilted square, as shown in Fig.  1(a). The square-octagon lattice has the same coordination number as the honeycomb lattice and enjoys the symmetry of the square lattice, which satisfies the C₄ point group.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. (a) Sketch map of square-octagon lattice and the cluster used in this work. (b) Sketch map of cluster embedded in self-consistent field for square-octagon lattice in cellular dynamical mean-field theory regime. (c) First Brillouin zone of square-octagon lattice with the high symmetry points Γ , M, and K. (d) Tight binding approximation energy dispersion along the line between high symmetric points in the first Brillouin zone of anisotropic square-octagon lattice for λ = 2.0. (e) Tight binding approximation energy dispersion along the line between high symmetric points in the first Brillouin zone of anisotropic square-octagon lattice for λ = 0.5.

The single band Hubbard model is used to investigate the effect of interaction, temperature, and anisotropic parameter on the quantum phase transition in anisotropic square-octagon lattice half-filled with fermions, and the corresponding Hamiltonian is

where and c_iσ represent creation and annihilation operators of fermions with spin σ on site i, respectively, while denotes the particle number operator on lattice site i. The value of spin index σ is spin up or spin down. The □ represents the square between two nearest different octagons. The first two terms in this Hamiltonian account for the kinetic energy of the system, which are characterized by the coefficient factors t₁ and t₂, respectively. The t₁ and t₂ are the hopping terms between the nearest neighboring sites in the same square lattice and between the endpoints of the liking line of the two nearest neighbor square lattices, respectively. An extra parameter named anisotropic parameter λ = t₁/t₂ is defined to describe the degree of anisotropy of square-octagon lattice. The third term describes the on-site repulsive interaction (U > 0) between fermions with opposite spins. Here we set t₁ as the energy unit (t₁ = 1). The μ is the chemical potential and required to be zero for half filling case.

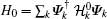
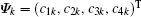
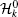
For U = 0 and μ = 0, the Hubbard model transmits to the tight-binding model and the Hamiltonian in the momentum space is , in which , takes the following form:

where a and b are the lattice constant related parameters and respectively equal to 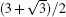and . The index i = 1, 2, 3, 4 in creation and annihilation operators represent the four sites in each unit cell as illustrated in Fig.  1(a), k is the location in the first Brillouin zone, and ↑ and ↓ hint at the spin-up and spin-down states, respectively. The energy dispersions of the anisotropic square-octagon lattice in the tight binding approximation have been shown in Figs.  1(c) and 1(d). The system is in the metal state while λ = 2.0 and in the insulating state while λ = 0.5.

Cellular dynamical mean-field theory (CDMFT)^{[18– 21]} as an extension of the dynamical mean-field theory is used to investigate the anisotropic square-octagon lattice with fermions. In comparison to the dynamical mean field theory, CDMFT gives more reliable simulation results for the low-dimensional system with strong quantum fluctuations due to its efficient consideration of the nonlocal effect. CDMFT maps the original square-octagon lattice onto a 4-site effective cluster embedded in a self-consistent bath field, as shown in Fig.  1(a). At the beginning of the self-consistent calculation process after mapping the lattice problem onto the impurity one, we guess a mini self-energy ∑ (iω ) which is independent of the momentum. Based on the initialized mini self-energy ∑ (iω ), the effective medium Weiss field g(iω ) can be obtained by the coarse-grained Dyson equation

where ω is the Matsubara frequency, μ is the chemical potential, ∑ _K is the summation all over the reduced Brillouin zone of the super-lattice, and t(k) is the Fourier-transformed 4-dimensional hopping matrix of super-lattice which is drawn from the square-octagon lattice in the scheme of cellular dynamical mean field theory. Continuous-time quantum Monte– Carlo algorithm^[22] is adopted as the impurity solver for obtaining the cluster Green» s function G(iω ) by simulating the effective cluster model. Cluster self-energy ∑ (iω ) is renewed by the Dyson function

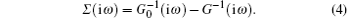
10⁷ Monte Carlo steps are executed in each iteration and the self-consistent iterative loop is repeated until the value of self energy difference reaches the expected accuracy.

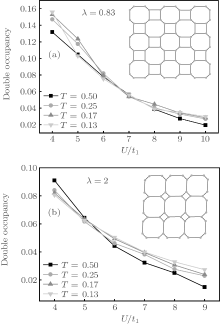
Double occupancy and density of state which are important to the study of the quantum phase transition in lattice systems are calculated and the phase diagrams, which are composed of on-site repulsive interaction and temperature, anisotropic parameter λ and on-site repulsive interaction are also presented. The double occupancy D_occ = ∂ F/∂ U = ∑ _i⟨ n_i↑ n_i↓ ⟩ /4 as a function of interaction U for various temperature and different hopping terms has been investigated, where F is the free energy. Figure  2 shows that the double occupancy increases with the decrease of anisotropic parameter λ at fixed interaction and temperature. It also can be found in Fig.  2 that the effect of temperature on the double occupancy is weakened with the increase of the on-site repulsive interaction due to the suppressing of the itinerancy of the atoms.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Double occupancy for different anisotropic parameter λ : (a) λ < 1, (b) λ > 1.

Fig.  3.

	Figure Option ViewDownloadNew Window
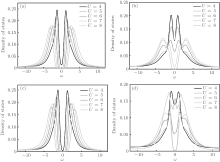	Fig.  3. Density of states for different interaction at (a) T = 0.25, λ = 2.0; (b) T = 0.25, λ = 0.83; (c) T = 0.17, λ = 2.0; (d) T = 0.17, λ = 0.83.

The single particle density of state ρ (ω ) (DOS) of anisotropic square-octagon lattice is calculated by the maximum entropy method.^[25] There is a big difference between the formation processes of pseudogap for T = 0.25 and T = 0.17 at λ = 0.83, while they are much similar at λ = 2.0. Pseudogap directly formed by splitting Fermi-liquid-like peak at λ = 2.0 without the appearance of the Kondo peak while at λ = 0.83 and T = 0.17, a pseudogap appears following after the appearance of the Kondo resonance peak, which is characterized by a sharp quasi-particle peak with two shoulders. At fixed temperature (T = 0.25), the critical on-site repulsive interaction for Mott transition is U_c/t₁ = 4.5 while λ = 2.0 and U_c/t₁ = 7.5 while λ = 0.83. The Kondo resonance peak formed at low temperature because of the effect between the local atom and the itinerant atom instead of that formed at higher temperature through splitting the Fermi-liquid like into two parts.

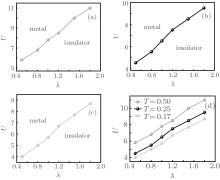
Effects of interaction and temperature on the quantum phase transition in the anisotropic square-octagon lattice with fermions are shown in Fig.  4, and the competition between anisotropic parameters λ and interaction between fermions in anisotropic square-octagon lattice are presented in Fig.  5. As Fig.  4 shows, the critical value of interaction will increase with the increase of λ for fixed temperature. From Fig.  5, we know that the critical value of anisotropic parameter λ for the Mott transition increases with the decrease of temperature for fixed interaction.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Interaction– temperature (U– T) phase diagram for different anisotropic parameter λ : (a) λ = 0.5, (b) λ = 1.0, (c) λ = 1.5. (d) Combination of the U– T phase diagrams for different λ .

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Anisotropic parameter– interaction (λ – U) phase diagram for different T: (a) T = 0.50, (b) T = 0.25, (c) T = 0.17. (d) Combination of the λ – U phase diagrams for different T.

We use the standard Hubbard model to describe the anisotropic square-octagon lattice with fermions and adopt the combination of cellular dynamical mean-field theory and continuous time Monte Carlo algorithm to solve the model. Based on the calculations of double occupancy and single particle density of states, we present the through discussion about the effect of interaction, temperature, and anisotropic parameter on the quantum phase transitions of an anisotropic square-octagon lattice with fermions. Results shows that the critical value of the interaction for quantum phase transition will increase with the increase of λ at fixed temperature and the critical value of anisotropic parameter λ for the Mott transition will increase with the decrease of temperature at fixed interaction.