Quantum key distribution (QKD)^{[1– 3]} provides a means of distributing secure keys between two remote parties, typically called Alice and Bob. In principle, QKD offers unconditional security guaranteed by the laws of physics.^{[4– 6]} Unfortunately, there is a big gap between the theory and practice of QKD. In the practical QKD system, the imperfection of the setups will leave some loopholes for Eve to spy on the secret key. In fact, some potential quantum attack strategies have been discovered by exploiting the imperfection of the sources and the single photon detectors, such as the PNS attack, Trojan horse attack, time-shift attack, blinding attack and so on.

In 2003, Hwang proposed a fundamental primitive decoy state QKD protocol^[7] against PNS attack, in which the yield of the single photon pulse can be estimated precisely by the transmission rates of different intensity sources, hence the key generation rate and the communication distance are both increased significantly. In 2004, Wang proposed a scheme to implement the decoy state QKD in practical quantum cryptography.^[8] Ma et al. also researched on the decoy state QKD^[9] and put forward a scheme in which the quantum key generation rate can reach the performance of infinite intensity sources with only three different intensity sources. Then, a series of decoy state QKD protocols have been proposed.^{[10– 17]} Decoy state is also used in the QKD protocol with heralded single-photon source^[14] and in the measurement device independent (MDI) QKD.^{[15– 17]}

Another important field of quantum communication is quantum secure direct communication (QSDC), whose object is to transmit the secret messages directly without establishing a key in advance to encrypt them. In 2002, Bostrom and Felbinger proposed a “ ping-pong” QSDC protocol using entanglement.^[18] In 2003, Wojcik present an eavesdropping strategy that was based on the Ping-Pong protocol, ^[19] which reduces the efficiency to 50 percent while introducing no error in the control mode. In 2013, Pavicic made a modification of Wojcik’ s attack, ^[20] ingenious unitary operations were performed on the travel photons to tell Bell states without introducing errors in the information mode.

In this paper, based on the circuit presented in Ref. [20], an extra modification is made to simplify the implementation of the operation. Moreover, this device is used to detect whether or not the input pulse is empty, and direct measurement is not performed when there is no more than one photon in the input state. Equipping this device at the receiver of QKD can reduce the impact of the dark count rate of the detector, hence increasing the communication distance.

The rest of this paper is organized as follows. A modification of the device is made in Section 2, and a simple analysis on detecting whether the pulse is empty or with a photon is also given. In Section 3, the modified device is equipped at the receiver of QKD with perfect single photon source (PSPS) to decrease the error induced by the dark count of the detector, therefore increasing the communication distance. Section 4 discusses the circumstance in which this device is used at the receiver of decoy state QKD with a weak coherent photon source (WCPS). Finally, some conclusions are drawn in Section 5.

This section describes a device which can be used to determine whether or not the input pulse is empty, and direct measurement is not performed when there is no more than one photon in the input state. A schematic diagram of the device is shown in Fig. 1. An ingenious unitary operation composed of two Hadamard gates, a PBS gate, and two CNOT gates is denoted as Q. The PBS gate lets the horizontally polarized photons through and reflects the vertically polarized ones. The half-wave plate (HWP) flips the polarization of the photon H ↔ V, which is mathematically written as

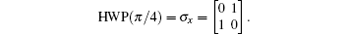
Two auxiliary modes (x and y) with only one photon in the state | vac⟩ _x| H⟩ _y are used in this article, where | vac⟩ _x denotes the x mode is empty.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of the device used to determine whether or not the pulse is empty.

Suppose that the state of the input photon is

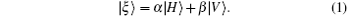
The initial state of the whole system can be expressed as

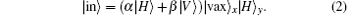
Upon applying the first two Hadamard gates H₁ and H₂, on x and y modes, the state of the whole system will read

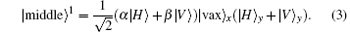
After this point, two CNOT gates exist in the Pavicic Mladen’ s scheme, ^[20] but considering that the state of the control photon will not influence the x and y modes, these two CNOT gates can be omitted. The same reason goes for Q^† . The PBS acting on the x and y modes, performs the following transformation:

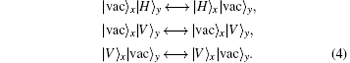
The whole system after the PBS₁ can then be expressed as

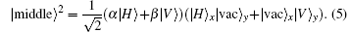
A CNOT gate has two inputs: the control bit and the target bit. When the control bit is 1, the target bit will be flipped, or the target bit will remain unchanged. The whole system after the CNOT₁ and CNOT₂ under the control of the input photon reads

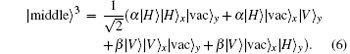
The operator HWP₁ yields the following state:

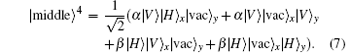
Similar to the analysis above, after the whole system passes through Q^† , we obtain

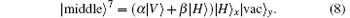
Applying HWP₂ on the input photon yields the final state of the whole system

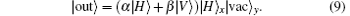
If there is no photon in the pulse, then the initial state of the whole system is

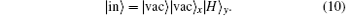
The final state of the whole system is

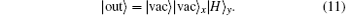
According to Eqs. (9) and (11), if a photon exists in the pulse, then there will be a detection in the x mode; if the pulse is empty, the y detector will click. The state of the input photon is not changed. In fact, this device can be seen as a non-demolition measurement device, from the detection result of the x and y modes, single-photon pulse can be distinguished from vacuum pulses. This can be used to improve the performance of the QKD protocol.

For long-distance QKD, the error mainly induced by dark count of the detector generally reaches about 0.5, thus secure key cannot be obtained. Considering the scenario that the device shown in Fig. 1 is equipped in the front of general detection setups, pulses arriving at the receiver will be used as the control mode of the device before going through the following detection setups. A click of the x pre-detector means that the following main detection result is caused by a photon with great probability, thus it is valid. Otherwise, a click of the y pre-detector means that the following main detection result is generally caused by a dark count, and it will definitely be deleted. With the help of pre-detection, only the valid detection result will be chosen, hence reducing the error rate.

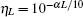
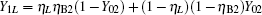
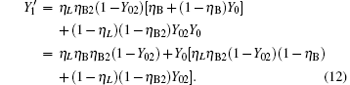
Suppose that the communication distance is L, the transmission probability of the channel is defined as , where the attenuation of fiber is described as α = 0.2 dB/ km. The probability a photon only cause a count in the x mode pre-detector is where η _B2 and Y₀₂ represent the detect efficiency and dark count rate of the pre-detector, respectively, and accordingly η _B and Y₀, respectively, represent the detect efficiency and dark count rate of the following main detector. The yield rate of every pulse of the whole system can be written as

Let e_d represent the total misalignment error rate, the error rate of the whole system can be written as

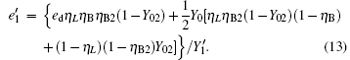
The yield rate and error rate of the original system reads

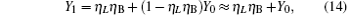
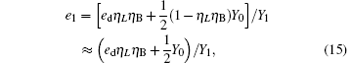
compared with η _B2, Y₀₂ is very small, so we have η _B2(1− Y₀₂) ≈ η _B2. For long-distance communication, η _L will be very small, thus obtaining

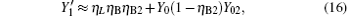
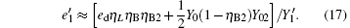
Compared with Eq. (14), equation (16) can be understood as the transmission probability that the single photon is attenuated by η _B2, the dark count rate is attenuated by (1 − η _B2)Y₀₂, so the yield of the source is decreased. In Eq. (15), at the communication distance when η _Lη _B = Y₀, since e_d ≪ 0.5, so the error is mainly induced by the dark count of the detector, the error rate is 25% ; with the distance increasing, η _Lη _B will be much smaller than Y₀, then the error rate will reach about 0.5, apparently the secure key cannot be obtained. While in Eq. (17), at the communication distance when η _Lη _Bη _B2 = Y₀(1 − η _B2)Y₀₂ the error rate will be 0.25, this communication distance of QKD is much larger than that of the original scheme. In this way, the effective communication distance of QKD can be increased greatly, this will be proved in the following simulation.

The final key generation rate can be calculated by the GLLP^[6]

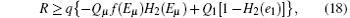
where q = 1/ 2, H₂(x) = − xlog₂(x) − (1 − x) log₂(1 − x), f(x) denotes the efficiency of two-way error correction. Due to the perfect single photon source, so Q_μ = Q₁ = Y₁, E_μ = e₁. Submitting Eqs. (12) and (13) into Eq. (18), we can get the key generation rate as the function of distance. The simulation parameters are selected coinciding with Ref. [21], they are e_d = 0.033, η _B = 0.045, Y₀ = 1.7 × 10^{− 6}, Y₀₂ = 1.7 × 10^{− 6}. The error rates of the sift key for the original QKD and the improved QKD proposed here are shown in Fig. 2. The final key generation rates for those two schemes are shown in Fig. 3.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The error rate of the sift key for different circumstances.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The final key generation rate for different circumstances.

Seen from Fig. 3, due to the pre-detection of the x mode, the final key generation rate is decreased, so the proposed scheme will not be suitable for a quantum communication whose distance is shorter than 160 km. From Fig. 2, we can see that the error rate is improved dramatically at a longer distance. Accordingly the communication distance will be increased significantly, as shown in Fig. 3, the improved QKD scheme with pre-detection mechanism can reach a communication distance of 516 km.

In the practical QKD, a WCPS source is generally adopted. Suppose the intensity of the source is μ , the number of photons existing in each pulse follows Poisson distribution

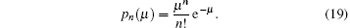
The yield of the pulse with no photon is

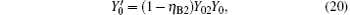
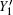
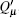
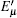
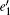
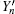
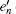
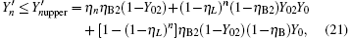
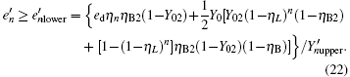
and equation (12) represents the yield of the pulse with only one photon. For a multi-photon pulse, probably more than one photon will arrive at the pre-detection device, there will be a detection in the x mode or y mode with certain probability. According to Eq. (18), in order to get the lower bound of R, the lower bound of and the upper bound of , , and should first be determined. Let η = η _Lη _B, for the original QKD scheme when Alice sends a pulse of n photon, the probability that at least one photon causes a count at Bob’ s detector is η _n = 1 − (1 − η )ⁿ. To calculate the yield of the n-photon pulse, first consider the case that the arriving multi-photon pulse causes a count in the pre-detector of x mode, the upper bound of and the lower bound of can be written as

In the other case assume that the arriving multi-photon pulse cause a count in the y mode of the pre-detector, we can then get the lower bound of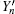

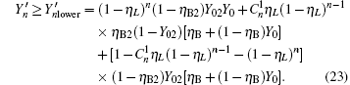
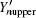
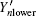
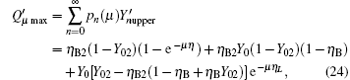
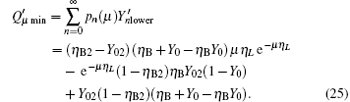
The difference between and is the processing of the multi-photon pulse: when the communication distance is long, the probability of a multi-photon arriving at the pre-detection device can be neglected because they will be the same as each other. The transmission probability of each pulse is given by

The maximum error rate of each pulse can be written as

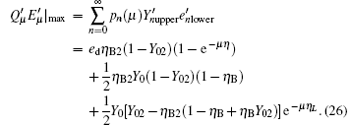
It is well known that decoy states can be used to improve the performance of QKD obviously. Based on this, we further analyse the performance of the decoy-state QKD with a pre-detection mechanism. A three-state protocol is utilized here, suppose that the intensity of three sources is μ ₁, μ ₂ and 0, respectively, and μ ₁ > μ ₂. The source with vacuum states is used to estimate the dark count rate

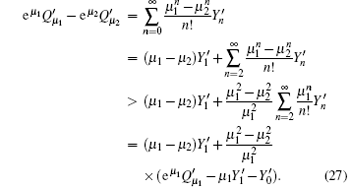
We can obtain the lower bound of the yield of a single photon pulse

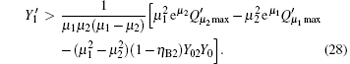
The gain of the single photon pulse is given by

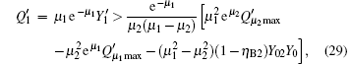
and the upper bound of the error rate can be estimated by

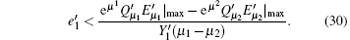
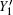
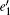
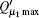
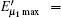
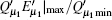
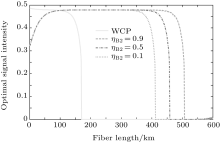
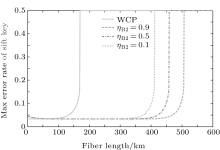
Then substituting , , , and into GLLP to simulate the performance of the three-state QKD protocol with pre-detection mechanism. In the simulation, the yield of the single-photon pulse is supposed to be estimated accurately, we can then get the optimal intensity of the signal source. Based on the optimal intensity of the signal source, the optimal intensity of the decoy state and the key generation rate can be obtained in turn.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The optimal signal intensity for different circumstances.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The max error rate of the sift key for different circumstances.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The final key generation rate for different circumstances.

The optimal signal intensity, the maximum error rate of the sift key, and the final key generation rate are shown in Figs. 4– 6, respectively. The green solid line shows the performance of the original decoy state QKD. The simulation results show that at the small communication distance, the Maximum error rate is a little bigger than that of the original QKD, because we give a loose estimate of the error come from multi-photon pulse. Thus, the optimal intensity is also lower to decrease the probability of multi-photon. Also, the final key generation rate is decreased due to the pre-detection of the x mode. The influence of multi-photon is decreased with the increase of the communication distance, the advantage of pre-detection is visible, the error rate is reduced dramatically, and the security distance can reach 479 km.

In this paper, we construct a circuit with PBS and CNOT gates, which can be used to determine whether or not the input pulse is empty according to the detection result of the auxiliary state, while the input state will not be changed. Equipping this device at the receiver can reduce the influence of the dark count of the detector for long-distance communication. Therefore, the secure communication distance can, respectively, reach 516 km and 479 km for QKD with PSPS and decoy-state QKD with WCPS, which has been shown in simulation results. When it comes to real-world implementation, synchronization of the signal with the auxiliary state and the main detector should be ensured, which can be realized with the help of the synchronization pulse in QKD protocol. The result of the main detector will be deleted if there is a corresponding detection in the y mode, the subsequent process is the same as QKD.