In recent years, quantum information has been a rapidly developing and emerging interdisciplinary science, including quantum computing and quantum communication.^{[1, 2]} The theory of quantum teleportation^[3] based on quantum entanglement is one of the applications of quantum communication.

Nowadays, many studies are based on pure states, such as maximally entangled state^{[4, 5]} and partially entangled states.^{[6, 7]} Given that the quantum system inevitably interacts with the environment, the decoherence effects will cause the loss of useful information more or less. That is, entanglement degradation and decoherence are unavoidable in quantum information processing, and thus pure state would degenerate into a mixed state. Teleportation using mixed states as an entanglement channel is, in general, equivalent to a noisy quantum channel, ^{[8, 9]} and the optimal teleportation fidelity is no longer unity.^{[10, 11]} Although purification schemes^{[12, 13]} may be applied to noisy channels, there exist some mixed states which have higher teleportation fidelity. An illuminating example is provided by the Werner states, ^[14] which is a convex sum of maximally mixed separable state and maximally entangled pure state.

Since the first experiment was realized in 1997, ^[15] a quantum teleportation distance of from tens of meters to 143 kilometers has been achieved by Ma et al.^[16] To achieve such a leap in long-distance quantum teleportation, quantum repeaters^{[17, 19]} are involved. Dur et al. ^[18] studied the use of N pairs Werner states for quantum communication over long distances, but they focused on purification. Entanglement swapping, ^{[20– 22]} which aims to establish entanglement between two distant nodes via intermediate nodes, is the basis of quantum repeaters and is of practical importance in quantum networks.

In this paper we propose the quantum wireless multihop network. In this network, quantum nodes which store quantum particles are distributed separately. There is usually no direct quantum channel shared between the source and destination nodes. The information is transmitted hop by hop via intermediate nodes. We consider the Werner state as the quantum channel^[23] from one node to another adjacent node, and we assume that the classical information to be teleported at the source node is a single quantum qubit.^[24] Generally, a mixed state can only be expressed by the density matrix and its computation is much more complicated than a pure state. Firstly, we deduce specific expression of the recovered qubit after one-hop teleportation. This recovered qubit is simultaneously the teleported state of the next-hop teleportation. With analogy calculations we obtain the recovered qubit after two-hop teleportation. Comparing the previous two expressions of the recovered qubits, there is a manifest similarity between them. We make an assumption and use mathematical induction to confirm this idea. Finally, we obtain the specific expression of the recovered qubit after multihop teleportation. Meanwhile, we have calculated the fidelity of each teleportation.

The rest of the paper is organized as follows. In Section 2, we discuss the quantum wireless multihop network. Detailed derivation and calculation of teleportation based on the Werner state are introduced in Section 3, including one-hop, two-hop, and multihop teleportation. Section 4 presents the conclusions.

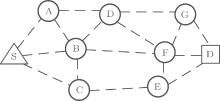
The quantum wireless multihop network^[25] that we have proposed in this paper is shown in Fig. 1. In this network, quantum nodes which store quantum particles are distributed separately.^[26] The information transmitted from the source node to the destination node in this network are the quantum bits (qubits) instead of the classical bits (c-bits) in the classical network. Generally, we use | y⟩ = a| 0⟩ + b| 1⟩ to model the qubit, where a and b are complex probability amplitudes satisfying | a| ² + | b| ² = 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Quantum wireless multihop network.

The two quantum nodes connected by dotted line are called neighbor nodes. The quantum wireless channel is only between neighbor nodes. In this paper we consider the neighbor nodes share for a Werner state as the quantum channel. The Werner state is a convex sum of maximally mixed separable state and maximally entangled pure state. The Werner state has many different forms. We consider ρ _W as the quantum channel.

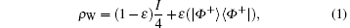
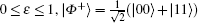
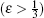
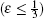
where is maximally entangled pure state. Depending on the weight ε , the Werner states may be entangled or separable . The Werner state is pure only when ε = 1.

The information qubit wants to be teleported from the source node to the destination node. As shown in Fig. 1, there is no direct quantum channel shared between S and D. The information can be transmitted hop by hop via intermediate nodes. There is more than one way from the source node to the destination node such as S– B– F– D, S– A– D– G– D, and S– C– E– D. A routing protocol is needed to select the appropriate path. According to the results we deduce in the subsequent paper, we can adopt the appropriate routing protocol^{[27, 28]} to optimize the transmission efficiency.

Quantum teleportation applies to transmit quantum states from one node to another separate node. Considering the practical significance of mixed states in quantum teleportation, it deserves to be conducted thorough research.

3.1. One-hop quantum teleportation based on Werner state

We first review the process of the standard quantum teleportation. The quantum circuit for one-hop teleportation based on the Werner state is shown in Fig. 2. The top two particles belong to Alice, while the bottom particle belongs to Bob. Alice first sends the teleported qubit and the particle shared from quantum channel to the controlled-NOT (CNOT) gate, followed by a Hadamard (H) gate on the first state. Quantum measurements are often performed as an intermediate step in a quantum circuit, and the measurement results are used to conditionally control subsequent quantum gates through the classical wireless channel. However, such measurements can always be moved to the end of the circuit as shown in Fig. 2. All of the classical conditional operations can be replaced by corresponding quantum conditional operations. The overall action of the two quantum circuits is the same.^[29] The measurement results go through the X gate and the Z gate, and then the teleported state can be recovered at Bob.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Quantum circuit for one-hop teleportation based on Werner state.

We assume that the sender (Alice) who has the first and second particles intends to send the first particle which is a single qubit

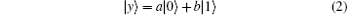
to the receiver (Bob) who has the third particle. In Eq. (2), a and b are complex and | a| ² + | b| ² = 1.

We assume the first particle to be in the initial state. The initial state’ s density matrix is

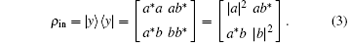
The second and third particles are in one of the Werner state 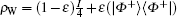in Eq. (1) as the quantum channel.

In the form of density matrix,

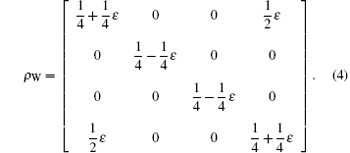
After the effect of quantum gates and the measurements, the state ρ _AB of three qubits that Alice and Bob have becomes

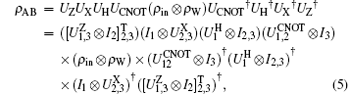
where 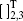is partial transpose on the 2nd and 3th qubits,

is controlled-Z (Z) gate,

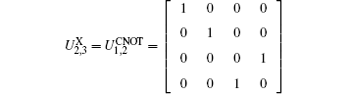
is the two-qubits CNOT gate, and is the H gate. We can see that U_Z, U_X, U_H, and U_CNOT are all real symmetric matrices, and their conjugate transpose matrices remain themselves.

The state ρ _out that reaches Bob is

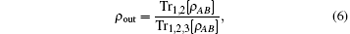
where Tr₁, 2[ ] is the partial trace over Alice’ s qubits.

Finally, we can calculate the result of one-hop teleportation straightforwardly. We set the output of one-hop teleportation based on the Werner state as ρ ₁

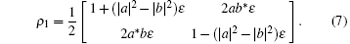
In order to quantify how much information which is preserved or lost during teleportation, we consider the fidelity

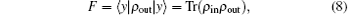
which is the square of the usual fidelity defined as

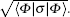
For our case, the one-hop teleportation fidelity based on the Werner state becomes

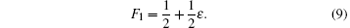
It is obvious that only when ε = 1, F₁ = 1 implies the perfect teleportation.

3.2. Two-hop quantum teleportation

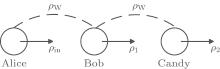
There is usually no direct quantum channel shared between the source and destination nodes. As shown in Fig. 3, we assume that Alice wants to teleport a quantum state to Candy. They share no direct quantum channel, but the intermediate node Bob shares quantum channel with Alice and another with Candy. Alice teleports ρ _in through Werner state between Alice and Bob, then Bob teleport ρ ₁ through Werner state between Bob and Candy. ρ ₂ is recovered at Candy. In this way, a quantum channel is established between Alice and Candy, which have never interacted with each other before.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Two-hop teleportation.

By inserting ρ _out into Eq. (8) and substituting ρ _in into Eqs. (5) and (6), we can obtain

With analogy calculations we can obtain the final system states in two-hop quantum teleportation.

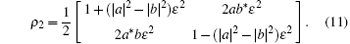
In this case, the fidelity of this hop teleportation alone is

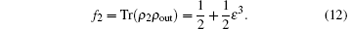
The fidelity of the whole two-hop teleportation becomes

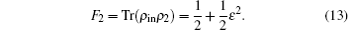
Obviously, the fidelity of two-hop hop teleportation is smaller than the single second hop teleportation.

3.3. Multihop quantum teleportation

Now we consider the case of multihop quantum teleportation, as shown in Fig. 4. From the above results of one-hop and two-hop teleportation, we can see some kinds of rules between Eq. (7) and Eq. (11). This idea can be proved by mathematical induction.

Proposition The output of n-hop teleportation is

Proof (i) When n = 1 and n = 2, equations (7) and (11) are proved to be true. (ii) When n = k − 1, we assume that the output of (k − 1)-hop teleportation or k-hop teleportation’ s input is

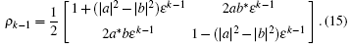
With the analogy calculations, we obtain the output of k-hop teleportation as

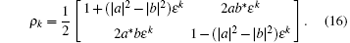
Compared with Eq. (14), the result is the same.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Multihop quantum communication.

Based on Proof (i) and (ii), for every natural number n (n > 0), the proposition is established and our conjecture is correct.

According to this conclusion, we can calculate the fidelity of this hop teleportation alone

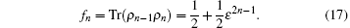
The fidelity of the whole multihop teleportation becomes

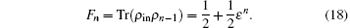
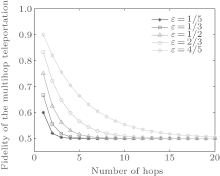
It should be noted that with the increase in the hops, the fidelity decreases, and is close to , as shown in Fig. 5. If ε = 1, equation (1) is a Bell state and F_n = 1. This is consistent with the conclusion that Bell states allow the perfect teleportation. In our case, the fidelity does not depend on the teleported state.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Fidelity of quantum wireless multihop network.

This result proves that quantum wireless multihop network based on the Werner state is similar to the classical network. With the increasing distance and hops, the probability of successful transmission will be reduced. In conjunction with Fig. 1, if we want to obtain the best transmission efficiency from the source node to the destination node, it is recommended to use the routing protocol based on the minimal hops principle.

In summary, we assume that a single qubit at the source node is teleported through multiple quantum channels based on the Werner state in a quantum wireless multihop network, and we derive the concrete expression of recovered state at the destination node using the method of mathematical induction. We also calculate for the fidelity of multihop teleportation. The results confirm the feasibility of quantum wireless network. There are still some issues worthy of study. This paper only deduces the Werner state as the quantum channel, a better result is to derive all of the mixed states. Meanwhile, the case of more particles^{[30, 31]} for the teleported state and the quantum channel is also worth studying. We hope that our approach may stimulate more investigations.