†Corresponding author. E-mail: cyttkl@cuit.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 61402058), the Science and Technology Support Project of Sichuan Province of China (Grant No. 2013GZX0137), the Fund for Young Persons Project of Sichuan Province of China (Grant No. 12ZB017), and the Foundation of Cyberspace Security Key Laboratory of Sichuan Higher Education Institutions, China (Grant No. szjj2014-074).
By using six-qubit decoherence-free (DF) states as quantum carriers and decoy states, a robust quantum secure direct communication and authentication (QSDCA) protocol against decoherence noise is proposed. Four six-qubit DF states are used in the process of secret transmission, however only the |0′⟩ state is prepared. The other three six-qubit DF states can be obtained by permuting the outputs of the setup for |0′⟩. By using the |0′⟩ state as the decoy state, the detection rate and the qubit error rate reach 81.3%, and they will not change with the noise level. The stability and security are much higher than those of the ping–pong protocol both in an ideal scenario and a decoherence noise scenario. Even if the eavesdropper measures several qubits, exploiting the coherent relationship between these qubits, she can gain one bit of secret information with probability 0.042.
Cryptography is the way to guarantee the safety of a secret message stored or communicated in the public environment. Both classical cryptosystems and quantum cryptography can solve the problems of security. However, the latter has shown the advantage of higher security because of the strong security basis assured by the physical principles. Therefore, quantum cryptography[1– 16] is now attracting a great deal of attention.
Quantum secure direct communication (QSDC) is a new concept in quantum cryptography which exchanges secret information securely using a quantum system. In a QSDC protocol, the secret message is transmitted directly without first establishing a key to encrypt it. In 2000, Long and Liu[5] developed an efficient pioneer two-step QSDC protocol. In that protocol, an Einstein– Podolsky– Rosen (EPR) pair is selected as the carrier qubit, and the qubits are transmitted in blocks, which improves the efficiency of eavesdropping detection. Later, many QSDC protocols[5– 16] were proposed. However, most researches about quantum secure communication are based on ideal scenarios.[1– 16] Noise is inevitable in a real scenario, which affects the safety and fidelity of the information exchanged. Therefore, studies of quantum cryptography in noisy scenarios are needed.
Channel noise is attracting a lot of attention.[17– 44] Researchers have found that the noises are usually caused by decoherence, which is caused by the coupling of a quantum system to its environment. Decoherence will make the quantum states fragile and easily destroyed, which leads to errors and leakage of secrets in the communication.[19] Collective decoherence is a kind of symmetry decoherence, which arises when the environment couples with the qubits without distinguishing between them.[19] For example, when the particles are delivered through some media such as the optical fiber, collective decoherence will appear. The alteration caused by collective decoherence can be described by a unitary operator U(t), where t denotes the time of transmission and indicates a temporal dependence. As mentioned in Ref. [20], if the time delay between the photons is small enough, the effect of collective noise on an N-qubit state can be modeled approximately as
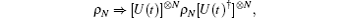
where [U(t)]⊗ N = U(t)⊗ · · · ⊗ U(t) denotes the tensor product of N unitary transformations U(t).
Many strategies have been proposed to decrease or eliminate the effect of decoherence noise, such as an error-correcting code (ECC), [21] quantum error correction, [22– 26] entanglement purification, [27– 31] entanglement concentration, [32– 38] and quantum error rejection.[40] However, those methods will not work well when the interaction with the environment is not weak enough and the qubits are not affected with a low probability, such as, when the strong collective decoherence exists.[19]
Decoherence-free (DF) states are some interesting states which are invariant under collective decoherence no matter how strong the interaction is.[19] DF states have been applied to the protection of quantum information in many researches. The invariance property of the DF state can be described by the following equation:
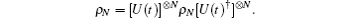
This immunity against [U(t)]⊗ N] has been demonstrated in some studies.[20]
In this study, a robust QSDCA protocol against decoherence noise is proposed based on six-qubit DF states. The six-qubit DF states are used not only as the quantum carrier but also as the decoy state. In the process of secret transmission, four six-qubit DF states are used as the carrier, however only the | 0′ ⟩ state is prepared; the other three six-qubit DF states can be obtained by permuting the outputs of the setup for | 0′ ⟩ . In the process of eavesdropping detection, the | 0′ ⟩ state is used as the decoy state; the detection rate and the qubit error rate reach 81.3%, which will not change with the noise level. The stability and security of the proposed protocol are much higher than those of the ping– pong protocol not only in an ideal scenario but also in the decoherence noise scenario. Most attacks including the man-in-the-middle attack, intercept-resend attack, Trojan horse attack, and coherent attack can be resisted in our protocol. If the eavesdropper performs the intercept-resend attack, he only has 7.86 × 10− 4% chance to know one bit of C, which will not lead to the leakage of M1, unless KA is leaked because of the improper storage by Alice and Bob. Even if the eavesdropper measures several qubits, exploiting the coherent relationship between these qubits, she can only gain one bit of secret information with probability 0.042.
In this section, four 6-qubit DF states[41– 44] are selected as the carrier qubits. They are in the forms of
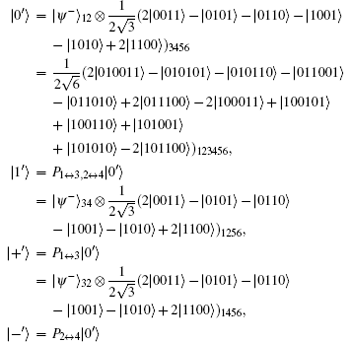
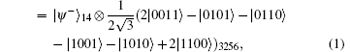
where 
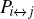


Here, {| 0′ ⟩ , | 1′ ⟩ } and {| + ′ ⟩ , | − ′ ⟩ } construct two orthogonal bases in the 6-qubit DF state space. Indeed, one can prepare these four mutually orthogonal 6-qubit DF states just by combining the two setups of Ref. [41]. By using six single-qubit measurements Z1Z2X3X4Z5Z6 (X1Z2Z3X4Z5Z6), we can distinguish | 0′ ⟩ and | 1′ ⟩ (| + ′ ⟩ and | − ′ ⟩ ), where Xi (Zi) (i = 1, … , 6) denotes measuring the i-th qubit in the X basis (Z basis).
Assume that Alice wants to send a secret message directly to Bob. The protocol is designed to help Alice and Bob finish their task safely. Alice and Bob share keys 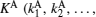
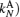
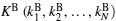
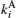
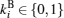
Step 1 By adding 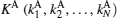
Step 2 Alice prepares photon sequence SC according to C(c1, c2, … , cN). Firstly, Alice prepares N | 0′ ⟩ states, which form qubit sequence S. If ci is 0, Alice randomly performs 1 ↔ 3 operation or nothing on the i-th | 0′ ⟩ state in S; if ci is 1, Alice randomly performs 1 ↔ 3 and 2 ↔ 4 operations or 2 ↔ 4 operation on the i-th | 0′ ⟩ state in S.
Step 3 Alice prepares other N | 0′ ⟩ states, which form a decoy photon sequence ST. To detect the eavesdropping, Alice mixes ST into SC according to a rule and sends the mixed sequence 
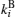
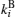
Step 4 After Bob receives 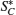
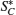
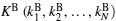
Step 5 If eavesdropping does not exist, Alice publicly announces the correct basis Z1Z2X3X4Z5Z6 or X1Z2Z3X4Z5Z6 of each 6-DF state in SC. Then Bob can measureSC correctly. According to the measurement result, Bob can restore C (c1, c2, … , cN). Then Bob obtains the secret message sent by Alice by adding 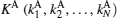
Step 6 Alice takes the next N bits of the secret message and begins the next transmission until all secret messages are sent.
In step 1, by adding 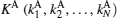
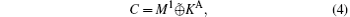
where 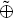

where PC denotes the permuting operations denominated by C, and S denotes the qubit sequence consisting of N | 0′ ⟩ states. After, Alice inserts decoy sequence ST to SC and obtains 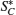
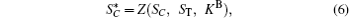
where Z denotes inserting ST to SC according to KB.
After Bob receives 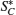
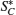

where Z− 1 denotes extracting ST from 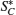

where Ms denotes measuring SC with bases Z1Z2X3X4Z5Z6 or X1Z2Z3X4Z5Z6. Bob obtains the secret message by adding 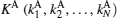
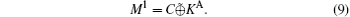
Obviously, the protocol is correct in the ideal scenario.
With the use of DF states, the collective decoherence noise will not lead to errors in the protocol. So only the noise other than collective decoherence needs to be considered. These noises might appear in all of the quantum preparation setups, quantum channels, and measurement equipment. Therefore, to protect our protocol from these non-collective decoherence noises, we can add an error-correcting code (ECC) in our protocol.
Alice and Bob select an [s, N] error-correcting code, [21] which uses an s bits codeword to encode an N bits word using generator matrix G(xN) and can correct t codeword error bits with the error-correcting function D(ys).
In step 1, after Alice obtains C, she calculates the corresponding bits codeword W= (w1, w2, … , ws), where
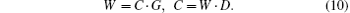
In step 2, Alice performs permuting operations on | 0′ ⟩ states according to W and forms a new qubit sequence SW,
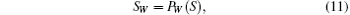
where PW denotes the permuting operations denominated by W, and S denotes the qubit sequence consisting of s | 0′ ⟩ states. After Alice inserts decoy sequence ST to SW, she obtains
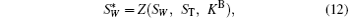
where Z denotes inserting ST to SW according to KB.
After Bob receives 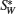
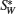
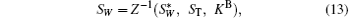
where Z− 1 denotes extracting ST from 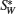
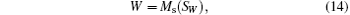
where Ms denotes measuring SW with bases Z1Z2X3X4Z5Z6 or X1Z2Z3X4Z5Z6.
Suppose that the non-collective decoherence noises appear in the courses of W (w1, w2, … , ws) as O = (o1, o2, … , os), where oi = 0 or 1 represents whether an error is existent or not in wi. Then Bob obtains bit string W’ as
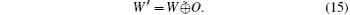
The C can be obtained by using the error-correcting function D(ys) on W’ ,
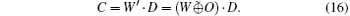
When the error rate does not exceed a rational threshold, the number of “ 1” in bit string O does not exceed t, therefore,
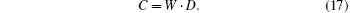
Bob obtains the secret message by adding 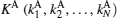
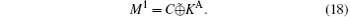
That is, the protocol is correct in the decoherence noise scenariotoo.
With the use of DF states, the protocol is immune to collective decoherence noise, therefore, the eavesdropping will be found more easily. The cryptanalysis of the QSDCA protocol boils down to two aspects: (i) how to analyze the eavesdropping detection rate if Eve eavesdrops; (ii) whether the protocol resists some common attack strategies, such as the intercept-resend attack, man-in-the-middle attack, Trojan horse attack, and coherent attack, or not. Because the identity authentication is implemented based on identity string KB, the protocol will not be threatened by the man-in-the-middle attack. Next we analyze the eavesdropping detection rate of the protocol and how the protocol resists some common attack strategies, such as the intercept-resend attack, Trojan horse attack, and coherent attack.
In the protocol, state | 0′ ⟩ is used as the decoy state to detect eavesdropping. Because the positions of decoy particles are secret, Eve cannot discriminate between decoy particles and information particles (particles in SC). Under this circumstance, Eve usually performs the same attack operation on all particles. We term the attack that Eve performs on each particle as E. Eve’ s attack will make the state | 0⟩ change to 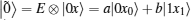
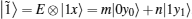
Because of Eve’ s attack, the combined system changes to
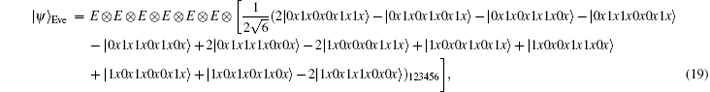

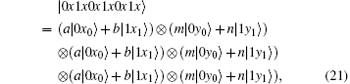
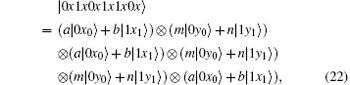

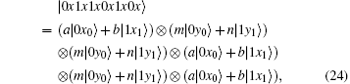
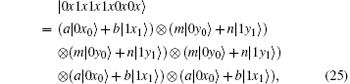
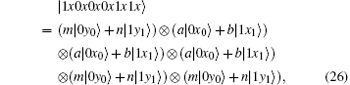
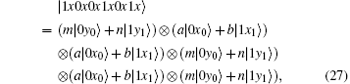
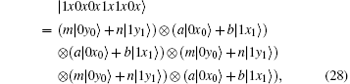
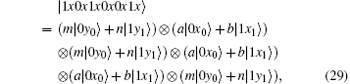
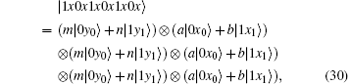
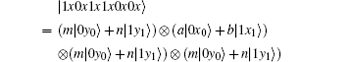
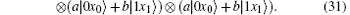
Obviously, after Bob receives 
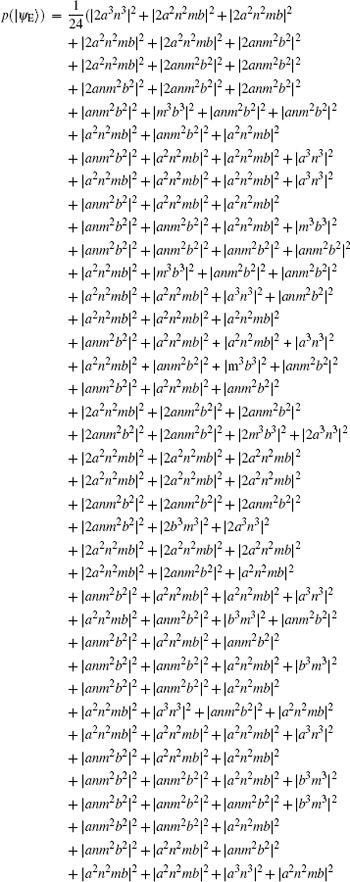
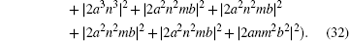
Suppose | a| 2 = s, | b| 2 = t, a = m, and b = n, then
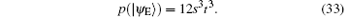
Because ∣ a∣ 2 + ∣ b∣ 2 = 1 and ∣ m∣ 2 + ∣ n∣ 2 = 1, p(∣ ψ E⟩ ) = − 12s6 + 36s5 − 36s4 + 12s3 can be obtained. Therefore, the error rate of each qubit due to eavesdropping is
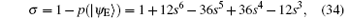
which can also be seen as the lower bound of the detection rate of each qubit eavesdropped,
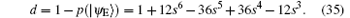
According to the theory of von Neumann entropy, the maximum amount of information contained in qubit | 0⟩ is termed as
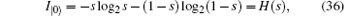
and the maximum amount of information contained in qubit | 1⟩ is termed as
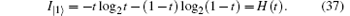
For a qubit transmitting in a quantum channel, it will be in the | 0⟩ or | 1⟩ state with equal probability (p = 0.5), therefore, the total information that Eve can eavesdrop in a qubit will be
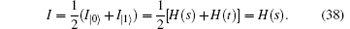
By calculating, when I = 1, d = 0.813 is obtained. Also σ = 0.813 can be obtained. That is, eavesdropping to obtain the whole message on one qubit will lead to an 81.3% qubit-error rate, whatever the noise level is. In Ref. [18], Li analyzed the security of the ping– pong protocol in the presence of collective-rotation noise (a major collective decoherence noise). According to Li’ s analysis, when the noise level is 0, the qubit-error rate caused by eavesdropping to obtain the whole message on one qubit is 0.5; when the noise level is 6%, the qubit-error rate is 0.18; and when the noise level is 11%, the qubit-error rate is 0.11. By comparing, we find that, when I = 1, the qubit-error rate in our protocol is always 81.3% whatever the noise level is; however, the qubit-error rate in the ping– pong protocol decreases dramatically with the increase of the noise level. Even when the noise level is 0, the qubit-error rate of the ping– pong protocol is only 0.5, which is much lower than that in our protocol. Therefore, the eavesdroppers will be found more easily in our protocol both in the ideal condition and the noisy condition. Even in the noisy condition, our protocol can display a better eavesdropping detection rate than the ping– pong protocol.
In an intercept-resend attack, when Alice sends particles to Bob, Eve intercepts some particles; Eve measures these individual particles and resends them to Bob. Eve intents to obtain some information by performing the intercept-resend attack. In this protocol, if Eve intercepts some particles, Eve has an 18.7% chance to guess the purpose of the particle right (for eavesdropping detection or transmitting secret information) and an 81.3% chance to guess wrong. If Eve guesses wrong, she cannot obtain any secret information contained in the qubit and is sure to be found. If Eve guesses right, Eve will have a 50% chance to choose the correct basis to measure the particle. Therefore, in this case, Eve has a 9.4% chance to know one qubit. Because six qubits contribute to one bit of C, Eve can know one bit of C with probability (9.4%)6 ≈ 6.89 × 10− 5%. However, because C is the result of M1 bitwise adding with KA, Eve cannot obtain the corresponding bit of M1 (the secret message) without KA (KA is secret to anyone else except Alice and Bob).
On the other hand, if Eve guesses right, but she chooses the wrong basis, Bob will have a 50% chance to obtain wrong information and Eve has a 50% chance to obtain the information. Under this circumstance, Eve has a 4.7% (18.7% × 50% × 50%) chance to know one qubit. Therefore, the total rate that Eve knows one qubit is 14.1% (9.4%+ 4.7%). Then Eve can know one bit of C with probability (14.1%)6 ≈ 7.86 × 10− 4%, which will not lead to leakage of M1, unless KA is leaked because of improper storage by Alice and Bob. Even if KA is leaked completely, Eve will have a 7.86 × 10− 4% chance to know the secret message on one qubit, which is much smaller than that in the ping– pong protocol (37.5%).
The KA and KB are shared by Alice and Bob by executing the QKD protocol, therefore KA and KB are safe in the process of quantum key distribution. In the process of secret transmission, KA and KB will never be delivered in classical form but in qubit form which will be unconditionally safe because of quantum mechanics. The only unsafe factor is improper storage of KA and KB by Alice and Bob. However, the loss of KA will lead to leakage of the secret message on one qubit with probability 7.86 × 10− 4%. The loss of KB will not lead to leakage of the secret message in this transmission but give Eve a chance to obtain KA by exhaustive attack, which will make leakage of the secret in the following transmission. Therefore, the loss of KB or both KB and KA will cause leakage of the secret.
The Trojan horse attack is performed by using spy photons. The spy photons are usually some invisible photons with a different wavelength or delay photons, which cannot be found by the legitimate users. Usually, Eve inserts spy photons to the legitimate photons. Because Bob cannot find the spy photons, Bob will encode the secret message on the spy photon, then Eve has the chance to obtain the secret message. In our protocol, Eve cannot obtain any secret message by performing a Trojan horse attack, because our protocol is a one-way protocol, Bob will not encode the secret message on photons.
In our protocol, | 0′ ⟩ and | 1′ ⟩ (| + ′ ⟩ and | − ′ ⟩ ) are distinguished by six single-qubit measurements Z1Z2X3X4Z5Z6 (X1Z2Z3X4Z5Z6). Bob measures 6-DF states in SC with basis Z1Z2X3X4Z5Z6 or X1Z2Z3X4Z5Z6. The decoy qubits mixed in SC are measured with basis Z1Z2Z3Z4Z5Z6. For measurements Z1Z2X3X4Z5Z6, X1Z2Z3X4Z5Z6, and Z1Z2Z3Z4Z5Z6, we can find that three single-qubit measurements, which are marked in bold, remain unaltered. If Eve wants to get some valuable information and escape from being detected, she can intercept all the states sent from Alice and only measure the qubits with Z2Z5Z6 except for the first, the third, and the fourth ones in each state.
| Table 1. All possible measurement results obtained by Eve with Z2Z5Z6 in her attack. |
All the possible measurement results obtained by Eve in this attack are shown in Table 1. From Table 1, we can see that when Alice sends | 0′ ⟩ and | + ′ ⟩ , Eve may obtain some results which will never appear in the cases | 1′ ⟩ and | − ′ ⟩ , i.e., ∣ 0⟩ 2∣ 0⟩ 5∣ 0⟩ 6 and ∣ 1⟩ 2∣ 1⟩ 5∣ 1⟩ 6. Here 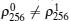
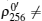

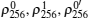

In many cases, six-qubit entangled states are very difficult to prepare and manipulate in an experiment. However, in our protocol, the 6-DF state | 0′ ⟩ can be prepared with a setup[43, 44] that can be designed by combining the two apparatuses of Ref. [41], and the other three states | 1′ ⟩ , | + ′ ⟩ , and | − ′ ⟩ can be prepared by permuting the outputs of the setup for | 0′ ⟩ .[42] The measurements of | 0′ ⟩ , | 1′ ⟩ , | + ′ ⟩ , or | − ′ ⟩ may be very difficult, however, six single-qubit measurements Z1Z2X3X4Z5Z6 (X1Z2Z3X4Z5Z6) cannot only distinguish | 0′ ⟩ and | 1′ ⟩ (| + ′ ⟩ and | − ′ ⟩ ), but also decrease the difficulty of measurement in an experiment. Therefore, our protocol is practical in an experiment.
We present a QSDCA protocol based on four six-qubit DF states. Because of the features of the four six-qubit DF states, only the state | 0′ ⟩ needs a setup and the other three states can be prepared by permuting the outputs of the setup for | 0′ ⟩ .[42] The protocol is verified as secure in the ideal scenario and the noise scenario. The four six-qubit DF states are immune to collective decoherence noise, however, they may be affected by some non-collective decoherence noises. To protect our protocol from these non-collective decoherence noises, we add an error-correcting code (ECC) in our protocol. The six-qubit DF state is not only used as the carrier to transmit a secret securely but also used as the decoy state to detect an eavesdropper. The detection rate (qubit error rate) reaches 81.3% per-qubit. Compared with the ping– pong protocol, the qubit error rate is much higher and is not effected by the noise level. The qubit-error rate in the ping– pong protocol decreases dramatically with the increase of the noise level. Most attacks including the man-in-the-middle attack, intercept-resend attack, Trojan horse attack, and coherent attack can be resisted in our protocol. If the eavesdropper performs an intercept-resend attack, he only has a 7.86× 10− 4% chance to know one bit of C, which will not lead to the leakage of M1, unless KA is leaked because of improper storage by Alice and Bob. Even if the eavesdropper measures several qubits, exploiting the coherent relationship between these qubits, she can gain one bit of secret information with probability 0.042.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|


