†Corresponding author. E-mail: fhym@ustc.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11175113), the Fundamental Research Funds for the Central Universities of China (Grant No. WK2060140013), and the Natural Science Foundation of Jiangsu Higher Education Institution of China (Grant No. 14KJD140001).
By virtue of the operator-Hermite-polynomial method, we derive some new generating function formulas of the product of two bivariate Hermite polynomials. Their applications in studying quantum optical states are presented.
In quantum mechanics and mathematical physics, the special function, the Hermite polynomial, is of fundamental importance. Physically, it is the eigenfunction of the harmonic oscillator.[1] In addition, by introducing a convenient complex form of the α -th two-dimensional fractional Fourier transform operation, it is found that the bivariate Hermite polynomial is a new eigenmode that propagates in quadratic graded index media.[2] Mathematically, the single-variable Hermite polynomial Hn(x) can be defined in terms of its generating function,
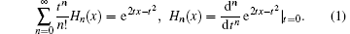
In Ref. [3], by combining the operator-Hermite-polynomials (OHP) method[4] and the technique of integration within an ordered product (IWOP) of operators, [5] we derived the generating functions of even and odd Hermite polynomials

when l = 0, 1. Since H0(x) = 1, H1(x) = 2x, we have

and these formulas are not only accumulated in mathematical handbooks but can also be useful in constructing some optical quantum states.[3] Furthermore, by introducing the Hermite-polynomial-operator Hn(X), where X is the coordinate operator (or the quadrature operator in quantum optics theory), and combining the IWOP technique, some new operator identities about quantum squeezing are derived, which are useful for studying the squeezed number state.[6] On the other hand, by replacing the arguments of the special function by quantum mechanical operators, a binomial theorem involving Hermite polynomials and a negative-binomial theorem involving Laguerre polynomials have been derived. These two theorems will have essential applications in quantum optics calculations, and the method is concise and helpful in deducing many operator identities, which may become a new branch in mathematical physics theory.[7] Using the entangled state representation, a two-mode squeezed number state can be converted into a Hermite polynomial excited squeezed vacuum state.[8] The generalized photon-added coherent state is obtained by repeatedly acting the combination of Bose creation and annihilation operations on the coherent state. It is found that it can be regarded as a Hermite excited coherent state due to its normalization factor related to Hermite polynomials.[9]
For the bivariate Hermite polynomials Hm, n(x, y) (note that Hm, n is not a direct product of two independent single-variable Hermite polynomials)[10]
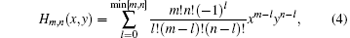
with the generating function in the form of
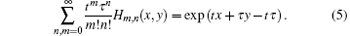
The bivariate Hermite polynomials Hm, n have their own applications in studying quantum optics. For example, in reference to the Weyl ordering
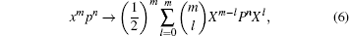
where X and P are coordinate and momentum operator, respectively. In Ref. [11], we examined the operators’ parameterized ordering and its classical correspondence, and found the fundamental function-operator correspondence

and its complementary relation

where the symbol : : denotes normal ordering.
In Ref. [12] we derived
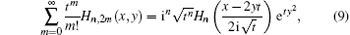
and
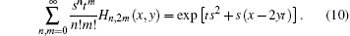
These two equations are the generating functions of Hn, 2m (x, y) and the more complicated one is

where A = 1 – 4st.
When k = l = 0, we have

In this work we shall derive some new generating function formula of the product of bivariate Hermite polynomials (PBHP), and we shall employ the OHP method to realize our goal. By the OHP method in this work, we aim to replace the classical Hermite polynomials Hm, n(x, y) by the operator ⋮ Hm, n(a† , a)⋮ first, where a† and a are the Bose creation and annihilation operator, respectively, obeying [a, a† ] = 1, ⋮ ⋮ denotes anti-normal ordering. By using
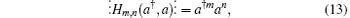
we can derive some operator identities in definite operator ordering (proof is given in Appendix A). Then we convert them back to the classical case. We also present some applications of these new generating function formulas of PBHP in quantum optics. Next, we shall briefly review the OHP method and exhibit its convenience and simplicity.
One of the fundamental operator identities in the OHP method is

where 
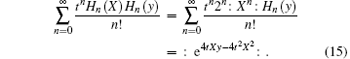
Again by using[13]
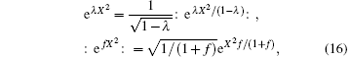
we have

Converting X back to x, we obtain
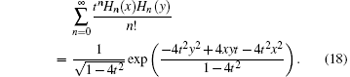
Thus, the merit of using the OHP method is fully displayed.
Now we prove the following one-index-summation of the product of two bivariate Hermite polynomials:
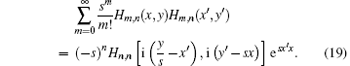
In this case, the OHP method we use is to replace Hm, n(x′ , y′ ) by ⋮ Hm, n(a† , a)⋮ .
Proof Rewrite Eq. (5) as
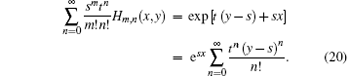
By comparing the same power term of tn/n! on the two sides we conclude

Then we employ the OHP method to consider the summation

where ⋮ Hm, n(a† , a)⋮ is in the anti-normal ordering form. Noting that a and a† are permuted within the anti-normal ordering symbol ⋮ ⋮ and using Eqs. (13) and (21) we can re-express Eq. (22) as

Then we need to change the right-hand side of Eq. (23) into anti-normal ordering for comparing with the left-hand side. Using the identity[14] which is responsible for converting an operator ρ (a, a† ) into its anti-normally ordered form
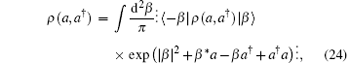
where | β 〉 = exp(− | β | 2/2 + β a† ) | 0〉 is a coherent state, 〈 − | β 〉 = e– 2| β | 2, we try to put (y – sa† )n (a – sx)n into its anti-normal ordering

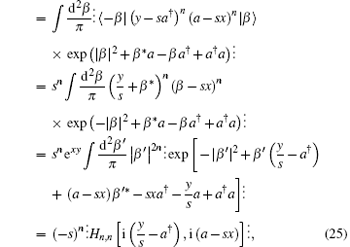
where in the last step we have used the integration formula
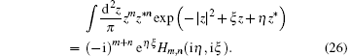
Substituting Eq. (25) into Eq. (23) we obtain
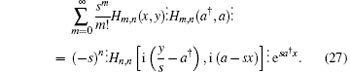
Since both sides in Eq. (18) are in anti-normal ordering and a† , a are commutable within ⋮ ⋮ , we can replace a† → x′ , a → y′ , leading to Eq. (19).
Based on the relation to the Laguerre polynomials
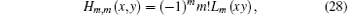
where

we can obtain
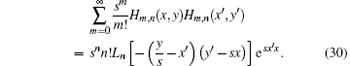
Similarly, we can prove
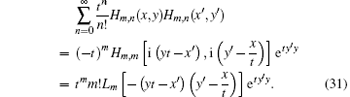
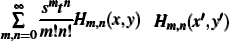
By using the generating function of Laguerre polynomials

we can further make summation 
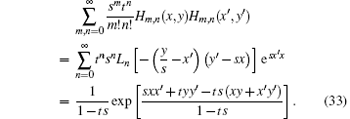
This formula can be used to derive
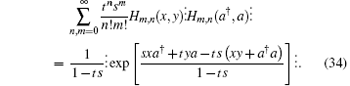
On the other hand, using Eq. (13) it is equal to

we obtain a new operator identity which links normal ordering to anti-normal ordering
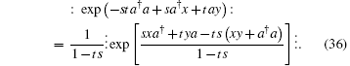
In particular, when x = y = 0,
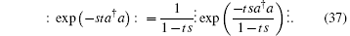
Next we examine the summation
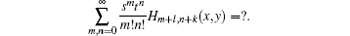
To proceed, using the OHP method and Eq. (13) we instead consider

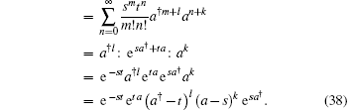
Using the binomial theorem regarding the bivariate Hemite polynomials[15]

we have

Thus, equation (29) becomes
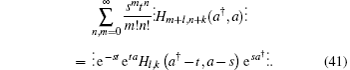
Since the both sides are in anti-normal ordering, we have
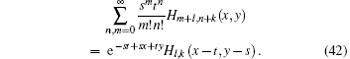
This is another type of generating function of bivariate Hermite polynomials.
As an application of Eq. (30), we consider the two-mode photon-subtracted squeezed vacuum state ambmS2(λ )| 00〉 , where S2(λ ) = exp [λ (a† b† – ab)] is the two-mode squeezing operator, with λ being a real squeezing parameter. The two-mode squeezed state is[15]
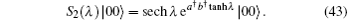
Using
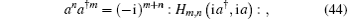
its derivation is shown in Appendix A. From Eq. (30), we obtain

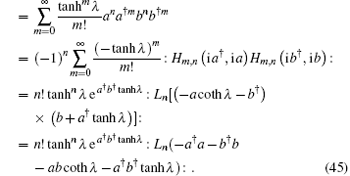
Thus, the two-mode photon-subtracted squeezed vacuum state can be expressed as

Therefore, | λ 〉 n is equivalent to Laguerre polynomial excitation on the two-mode squeezed vacuum state. In Ref. [16], we calculated its normalization factor

where Pm(x) is the Legendre polynomial

Using Eqs. (46) and (47) as well as the coherent state’ s completeness relation 
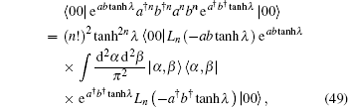
so

which is a new integration formula.
As an application of Eq. (33), we obtain
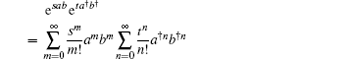

which changes the anti-normally ordered form esab eta† b† into its normal ordering, or

Then we turn to an application of Eq. (42) in quantum optics. We consider the following state vector which is generated by operating Hl, k (ξ – b† , ξ * – a† ) on the entangled state | ξ 〉 , where
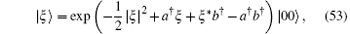
which takes the bivariate Hermite polynomials Hm, n(ξ , ξ * ) as its expansion function in the two-mode Fock space

| ξ 〉 obeys[18]

so

In comparison with Eq. (42) we see
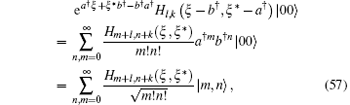
where 
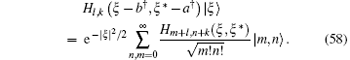
It follows the Fock space wave function of Hl, k (ξ – b† , ξ * – a† ) | ξ 〉 that

In summary, by virtue of the OHP method and the IWOP technique, we have derived some new generating function formulas about the bivariate Hermite polynomials. Their applications in studying quantum optics are presented as well.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|


