†Corresponding author. E-mail: rez.mohammadi@gmail.com, mohammadi@neyshabur.ac.ir
The aim of the present paper is to present a numerical algorithm for the time-dependent generalized regularized long wave equation with boundary conditions. We semi-discretize the continuous problem by means of the Crank–Nicolson finite difference method in the temporal direction and exponential B-spline collocation method in the spatial direction. The method is shown to be unconditionally stable. It is shown that the method is convergent with an order of
Nonlinear partial differential equations are useful in describing various phenomena in applied mathematics and physics. Analytical solutions of these equations are usually not available, especially when the nonlinear terms are involved. Since only limited classes of the equations are solved by analytical means, numerical solutions of these nonlinear partial differential equations are of practical importance (see Refs. [1]– [5]). Solitary waves are wave packets or pulses, which propagate in nonlinear dispersive media. Due to the dynamical balance between the nonlinearity and the dispersive effects, these waves retain a stable waveform. A soliton is a very special type of a solitary wave, which propagates without any change of its shape and velocity properties after collisions with other solitons. The present work is concerned with the numerical solution of the regularized long wave (RLW) equation, which was first derived by Peregrine to define undular bore development.[6] Since then, this equation has been used to model a large number of problems arising in various areas of applied science. The RLW equation is an alternative description of nonlinear dispersive waves to the more usual Korteweg– de Vries (KdV) equation. It has been found to have solitary wave solutions and govern a large number of important physical phenomena such as nonlinear transverse waves in a shallow water, ion-acoustic, magneto-hydrodynamic waves in plasma and phonon packets in nonlinear crystals, anharmonic lattices, longitudinal dispersive waves in elastic rods, pressure waves in liquid– gas bubble mixtures, rotating flow down a tube, the lossless propagation of shallow water waves, and thermally exited phonon packets in low-temperature and nonlinear crystals.[7– 9] Indeed, the RLW equation is a special case of the generalized regularized long wave (GRLW) equation, which is given by
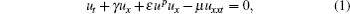
where p is a positive integer, 
The solutions of this kind of equations are important in many applications. However, for more general initial conditions, the theoretical solutions for these equations are limited. Therefore, many researchers have put in a great deal of effort to compute the solutions of these equations using various numerical methods and the numerical solutions of the initial and initial-boundary problems of the nonlinear GRLW equation.
Bona et al.[11] investigated the Fourier spectral method for the initial value problem of the GRLW equation. The method of lines based on the discretization of the spatial derivatives by means of Fourier pseudo-spectral approximations for the GRLW equation was derived by Durá n and Ló pez– Marcos.[12] Djidjeli et al.[13] discussed a linearized implicit pseudo-spectral method for the RLW equation. Adomian decomposition method was implemented for finding the solitary-wave solutions of GRLW equation by Kaya and El. Syed.[14, 15] Zhang[16] developed an implicit second-order accurate and stable energy preserving finite difference method based on the use of central difference equations for the time and space derivatives for GRLW equation. A numerical method for the GRLW equation using a reproducing kernel function was studied by Xie et al.[17] Jafari et al.[18] used sine– cosine and tanh methods to obtain the solutions of the GRLW equation. Mokhtari and Mohammadi[19] presented a mesh-free technique based on sinc basis functions for the numerical solution of the GRLW equation. In addition, they proposed a new iterative algorithm for solving the GRLW equation.[20] Feng et al.[21] presented a mesh-less method for the nonlinear GRLW equation based on the moving least-squares approximation. The GRLW equation is solved numerically via the Petrov– Galerkin method by Roshan.[22] Their method uses a linear hat function as the trial function and a quintic B-spline function as the test function. Lin[23] presented a numerical method based on parametric adaptive cubic spline functions for solving the GRLW equation.
The RLW equation is an important equation in physics media describing phenomena with weak nonlinearity and dispersion waves.[24] Recently, many well-known numerical techniques, such as finite element methods based on the least square principle, [25– 27] finite element methods based on the Galerkin and collocation principles, [28– 36] the Petrov– Galerkin method, [37] the radial basis functions collocation method, [38, 39] B-spline differential quadrature methods, [40] mesh-less methods, [41] Galerkin and collocation methods, [42– 45] the spectral method[46] and non-polynomial spline method[47] are employed to solve the RLW equation.
The RLW equation possesses only three invariant constants of motion corresponding to conservation of mass, momentum, and energy given by[48]

The MRLW equation is another particular case of the GRLW equation for p = 2. Gardner et al.[48] used a collocation method with quintic B-splines for the numerical solution of the MRLW equation. Khalifa et al.[49] applied a finite difference method to study solitary waves for the MRLW equation, and showed that the scheme is marginally stable. The MRLW equation is solved numerically via a collocation method using cubic B-splines finite element by Khalifa et al.[50] Khalifa et al.[51] used the Adomian decomposition method for solving the MRLW equation. Ali[52] has developed a classical radial basis function collocation method for solving the MRLW equation. Raslan[53] used the quadratic B-spline function and a central difference operator for the time derivative to develop a new algorithm based on the collocation method to solve the MRLW equation. A computational comparison study of quadratic, cubic, quartic, and quintic splines for solving the MRLW equation is presented by Raslan and Hassan.[54] Raslan and EL-Danaf[55] used the B-spline finite element method to solve the MRLW equation. The numerical scheme based on the quartic B-spline collocation method is designed for the numerical solution of the MRLW equation by Haq et al.[56] Achouri and Omrani[57] used the homotopy perturbation method to implement the MRLW equation with some initial conditions. The MRLW equation, with some initial conditions, is solved numerically via a variational iteration method by Labidi and Omrani.[58] Dereli[59, 60] simulated traveling wave solutions of the MRLW equation using the mesh-less method based on collocation with well-known radial basis functions. Khan et al.[61] employed the homotopy analysis method to obtain an approximate numerical solution of the MRLW equation with some specified initial conditions. Karakoc et al.[62] obtained a numerical solution of the MRLW equation based on the quintic B-spline collocation method over the finite elements.
The MRLW equation also has three conservation laws related to mass, momentum, and energy[49]

The spline function is a piecewise continuous polynomial function suitable to approximate an arbitrary function. It is known to approximate an arbitrary function better than other polynomial functions with the same degree. Spline functions are used in many applications such as interpolation, data fitting, and numerical solution of ordinary and partial differential equations. Rashidinia and Mohammadi[63, 64] derived approximate expressions for the dispersion relation of the nonlinear Klein– Gordon and sine– Gordon equations in the case of strong nonlinearities using a method based on tension spline functions and finite difference approximations. Also, Mohammadi developed explicit methods using exponential spline functions and finite difference approximations for the numerical solution of the generalized Burgers’ – Fisher, [65] convection– diffusion, [66] nonlinear Schrö dinger, [67] and Euler– Bernoulli beam[68] equations. Chegini et al.[47] employed non-polynomial spline basis functions to obtain approximate solutions of the RLW equation. Bian[69] used the Crank– Nicolson (C– N) method combined with a B-spline basis set for time-dependent and time-independent calculations of the photoionization cross sections of atoms and molecules.
In this work, we use exponential B-spline collocation and Crank– Nicolson methods for the numerical study of the GRLW equation. Our main objective is to improve the accuracy of the cubic B-spline method by utilizing some parameters, which enable us to obtain various classes of methods. Our method is a modification of the cubic B-spline method for the numerical solution of Eq. (1). Application of our method is simple. While solving initial boundary value problems in partial differential equations, the procedure is to combine a spline approximation for the space derivative with a Crank– Nicolson finite difference approximation for the time derivative. The combination of a finite difference and an exponential spline functions technique provides better accuracy than finite difference methods. Therefore, the time derivative is replaced by a finite difference representation and the space derivatives by exponential B-splines. We use the exponential B-spline basis that leads to the tri-diagonal nonlinear system which can be solved by well known algorithms such as the Newton algorithm. Numerical examples are presented, which demonstrate that the present scheme with exponential B-splines gives more accurate approximations than the scheme using cubic B-splines. Our method is a user friendly, economical and stable method for GRLW equation.
The rest of this article is organized as follows. In Section 2, the B-spline basis for the space of exponential splines is given and some interpolation results for exponential splines are stated. In Section 3, the construction of the exponential B-spline collocation method for the numerical solution of GRLW equation is described. In Section 4, the stability analysis is theoretically discussed. Using the Von Neuman method, the proposed method is shown to be unconditionally stable. Section 5 is devoted to the convergence analysis of our presented method. The method is shown to have second-order convergence. In Section 6, numerical examples are included to illustrate the practical implementation of the proposed method. The accuracy performance of the obtained numerical results are compared to the exact solution and other existing methods. The numerical results show that our proposed method is a promising approach for solving different types of these non-linear partial differential equations problems. Finally, we conclude our paper in Section 7.
For an interval [a, b], we divide it into n subintervals [xi, xi + 1] (i = 0, 1, … , n – 1) by the equidistant knots xi = a + ih (i = 0, 1, … , n), where h = (b – a)/n.
A function 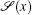

Among various classes of splines, the polynomial spline has received great attention primarily because it admits a basis of B-splines which can be accurately and efficiently computed. It has been shown that an exponential spline also admits a basis of B-splines which can be defined as follows. Let Bi(x) be the B-spline centered at xi and have a finite support on the four consecutive intervals 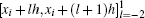

where

and
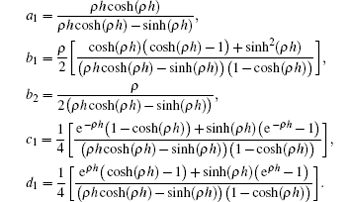
Each basis function Bi(x) is twice continuously differentiable.
Let s(x) be the cubic spline and 
Theorem 1 
Following Ref. [74] we obtain the following theorem.
Theorem 2 
These theorems together with the de Boor– Hall error estimate[75] lead to the following corollary.
Corollary 1 if u(x, t) ∈ C4[a, b], then there exists a constant, χ i, independent of h such that
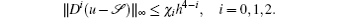
In this section, we consider the initial-boundary value problem of the GRLW equation
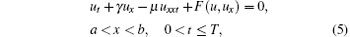
with the initial condition

and the boundary conditions

where F(u, ux) = ε upux, γ , ε , and μ are positive parameters, and ϕ (x), f0(t), and f1(t) are known functions.
The domain [a, b] × [0, T] is divided into an n × m mesh, with 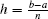
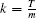
Now, we use the horizontal method of lines to discretize the time variable by means of the Crank– Nicolson method with a constant step size k, keeping the space variable x continuous. This semi-discretization yields the following system of nonlinear ordinary differential equations:

with the boundary conditions

We can rewrite Eqs. (8) and (9) as

where
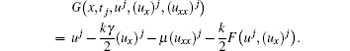
Let U(tj+ 1) be the exact solution and u(tj+ 1) the approximate solution of problem (10) at the (j + 1)-th time level, the local truncation error of the time semi-discretization method is given by ej+ 1 = U(tj+ 1) – u(tj+ 1). The local error estimate of each time step contributes to the global error in the temporal discretization, which is defined, at tj, as 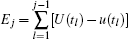
Lemma 1 if

then the local truncation error associated to the semi-discrete scheme (8) satisfies

and the global truncation error at time tj satisfies

Proof Because u is adequately smooth and 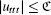
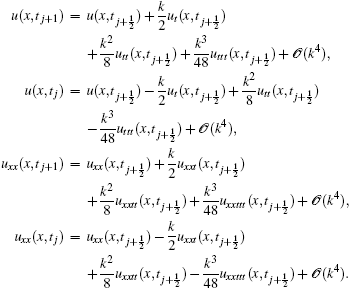
With the help of the above equations, one can obtain
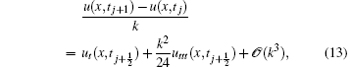
and

Using Eqs. (5), (13), and (14), we have

Moreover, as
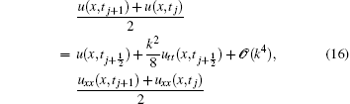

and
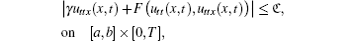
we have

From Eqs. (15) and (18), we deduce that
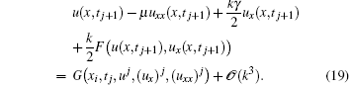
Using the mean-value theorem we rewrite Eq. (19) as
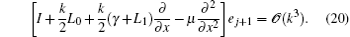
Now following Ref. [76] we obtain
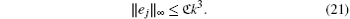
Using the local error estimate up to the j-th time step given by Eq. (21), we obtain the following global error estimate at the j-th time step:

which gives the second-order convergent of the method in time direction.
Let Bi (i = – 1, 0, … , n + 1) be the exponential B-splines with both knots xi and two additional knots outside the region, positioned at x– 1 < x0 and xn < xn+ 1. The set of exponential B-splines B– 1, B0, … , Bn+ 1 forms a basis for functions defined over the problem domain [a, b]. The exponential B-splines (4) and their first and second derivatives vanish outside the interval [xi– 2, xi+ 2].
An approximate solution u(x, t) to the analytical solution U(x, t) will be sought in the form of an expansion of B-splines

where ς i are time-dependent parameters to be determined from exponential B-spline collocation form of Eq. (1).
At knots, nodal values and their principal first and second derivatives are obtained in terms of the time parameters using exponential functions (4) and the approximate solution u(x, t) as
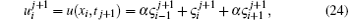
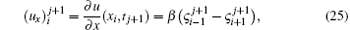

where
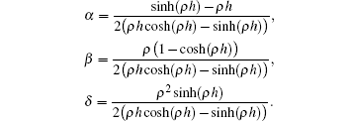
If we substitute the global approximation (23) and its necessary derivatives (24)– (26) at the knots in Eq. (10), we obtain the following difference equation with the variables ς :
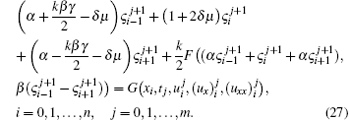
System (27) consists of (n + 1) equations in the unknowns 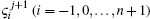
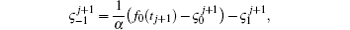
and
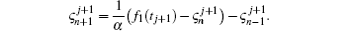
Putting i = 0, n in Eq. (27) and using the above notations we obtain two additional equations
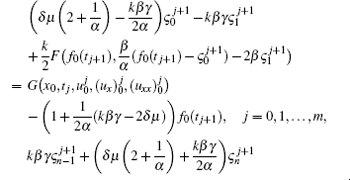
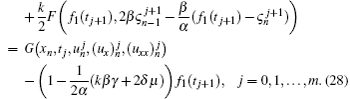
Equations (27) and (28) can be written in the matrix form as follows:
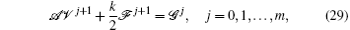
where
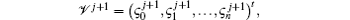
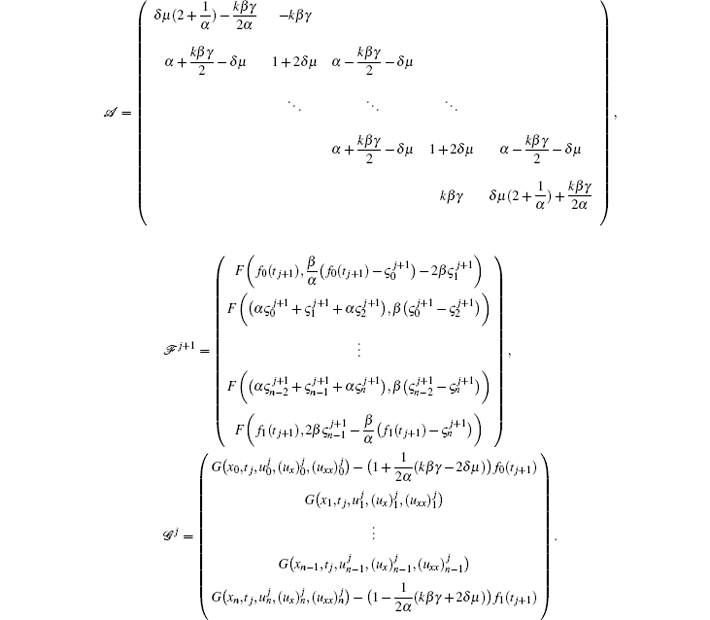
The above (n + 1) × (n + 1) nonlinear matrix system is solved using the Newton method. The starting vector is chosen to be zero.
To obtain the solution parameters, it is necessary to find the initial vector u0. To do this, the initial condition (6) uses the following expression:

After obtaining the initial vector u0, at the next time step the time vectors 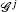
For stability analysis, following Refs. [35], [47], [48], [50], [56], and [79] and the references therein we use the Von Neumann method. The nonlinear term F(u, ux) cannot be handled by the Fourier mode method, so we must linearize it by making 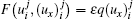


where ψ is the mode number, 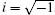

we obtain

where
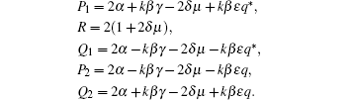
After simple calculations, equation (32) becomes
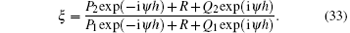
Using Euler’ s formula, that is, exp(iψ h) = cos (ψ h) + i sin (ψ h), equation (33) can be rewritten as

This equation can be rewritten as

For stability, we must have | ξ | ≤ 1, otherwise ξ j in (31) would grow in an unbounded manner, that is,

Since the numerator in Eq. (36) is smaller than the denominator, | ξ | ≤ 1, and this method is unconditionally stable, it means that there is no restriction on the grid size, i.e., on h and k, but we should choose them in such a way that the accuracy of the scheme is not degraded.
In this section, we prove that the exponential B-spline collocation method has uniform convergence of order two in the spatial domain for our problem. For the derivation of uniform convergence we first prove the following lemma.
Lemma 2 The exponential B-splines { B– 1, B0, … , Bn+ 1} defined in Eq. (4) satisfy
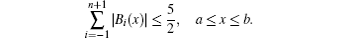
Proof See Ref. [71] for proof.
Theorem 3 Let u(x, t) be the collocation approximation from the space of exponential B-splines to the solution U(x, t) of the GRLW equation problem (5)– (7). Then the uniform error estimate is given by
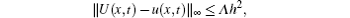
where Λ is a positive constant independent of h.
Proof Let u(x, t) be the unique exponential spline collocation approximate solution of Eqs. (5)– (7), which is given by
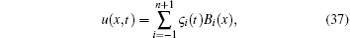
and let ũ (x, t) be the unique exponential spline interpolation from the space of exponential B-splines to the exact solution U(x, t) of Eqs. (5)– (7), which is given by
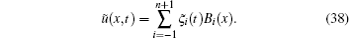
From Eq. (29) for u(x, t) and ũ (x, t) we have

where 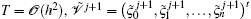
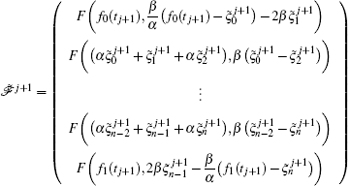
From Eq. (39) we obtain
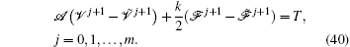
Now we consider the nonlinear term in the left hand side of Eq. (40). Following Ref. [77] and [78] and using the mean-value theorem, we have
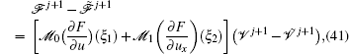
where ξ 1, ξ 2 ∈ (a, b),
and

From Eqs. (40) and (41), we have

where

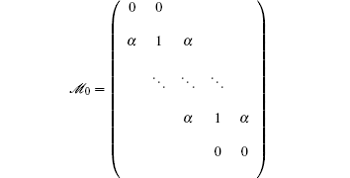
It is easy to see that for sufficiently small h, 𝔇 is a monotone matrix and hence invertible, so from Eq. (42) we have

Using the infinity norm yields

Clearly, the row sums 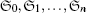
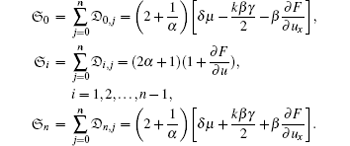
Moreover, from the theory of matrices, we have
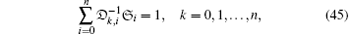
where 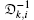
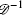
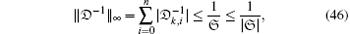
where

Also following Corollary 2.3, there exists a constant χ such that ||T||∞ ≤ χ h2. Now by substituting Eq. (46) into Eq. (44), we have
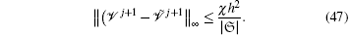
Moreover, as

Thus, combining Eqs. (47) and (48) and Lemma 2, we have

From Corollary 1, we deduce that
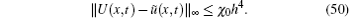
Generally, we have ||U(x, t) – u(x, t)||∞ = ||U(x, t) – ũ (x, t)||∞ + ||ũ (x, t) – u(x, t)||∞ . According to the above notations we deduce the stated result as
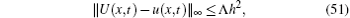
where 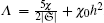
Theorem 4 Let U(x, t) be the solution of the initial boundary value problem (5)– (7) and u(x, t) be the collocation approximation to the solution U(x, t) after the temporal discretization stage. Then under the hypothesis of Lemma 1 and Theorem 3 the error estimate of the totally discrete scheme is given by

where 
To illustrate the effectiveness of the exponential spline collocation method (29), numerical results portraying a single soliton solution and the collision of two solitons are reported for different GRLW equations. The numerical results obtained are compared with the analytical solution, each providing corroborative evidence of the findings of the other. The accuracy of the scheme is measured by using the following error norms:
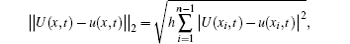
and
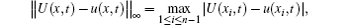
where U(x, t) and u(x, t) represent the exact and approximate solutions, respectively.
Moreover, the quantities 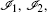


for the RLW equation and in a similar manner for the MRLW equation as

The analytical solution of the GRLW equation is given by
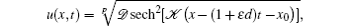
where

which corresponds to a solitary wave of amplitude 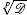
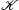
The RLW equation in the regions [− 40, 60] and [− 80, 120] ford = 0.1 and d = 0.03 was integrated from t = 0 to 20 with x0 = 0 and different values of k and h. The L∞ and L2 errors and invariants 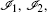
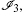
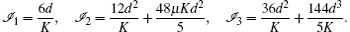
Throughout the simulation, L2 and L∞ error norms remain less than 7.950152 × 10– 5 and 4.207305 × 10– 5 (for d = 0.1), and 1.157133 × 10– 5 and 4.174280 × 10– 6 (for d = 0.03). In comparison with the analytical values, it can be seen from Tables 1 and 2 that the quantities 

| Table 1. Errors and invariants for single soliton of the RLW equation with d = 0.1, through the interval [− 40, 60] at time t = 20. |
| Table 2. Errors and invariants for single soliton of RLW equation with d = 0.03. |
Now we study the motion of a single solitary wave of the MRLW equation. For the sake of comparison with other existing methods, we take d = 1, 0.3, and x0 = 40 in the region 0 ≤ x ≤ 100. The L∞ and L2 errors and invariants 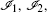

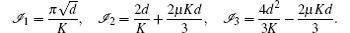
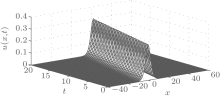
Throughout the simulation the L2 and L∞ error norms remain less than 2.3909 × 10– 3 and 1.0647 × 10– 3 (for d = 1), and 1.3378 × 10– 4 and 6.1250 × 10– 4 (for d = 0.3). A comparison with the methods in Refs. [22], [48], [50], [52], [53], [56], and [62] shows that the error norms at times t = 10 and 20, obtained with the present method, are smaller than those obtained with other existing methods (see Table 3). From this Table, it can be seen that the conservation properties (using the exponential spline collocation method) are very good. In comparison with the analytical values for the invariants, for d = 1 and d = 0.3, the relative changes in the invariants are very small. This degree of conservation is superior to that found with the other methods listed in Table 3. The profile of the solitary waves for the MRLW equation with d = 0.3, from time t = 0 to 20, are depicted in Fig. 2.
 | Fig. 2. Space– time graph of the single solitary wave up to t = 20 s, with d = 0.3, k = 0.01, and h = 0.1, for the MRLW equation, through the interval [0, 100] for x0 = 40. |
| Table 3. Invariants and errors for single soliton of the MRLW equation for x0 = 40, 0 ≤ x ≤ 100, and different values of d, t, h and k. |
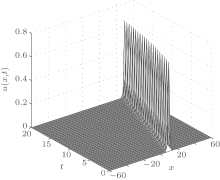
For the purpose of illustration of the presented method for solving the GRLW equation, we consider the case for p ≥ 3 in [− 60, 60] for x0 = 10. In this test, calculations are carried out with d = 1.01, k = 0.1, h = 0.48, and (p = 4, 6, 8, 10 when the final time is t = 10. Errors in L2 and L∞ norms at several times are listed in Table 4 and compared with results in Ref. [21]. The plot of the estimated solution with d = 0.3 and p = 10, from time t = 0 to 20, are shown in Fig. 3. Throughout the simulation the L2 and L∞ error norms remain less than 1.8 × 10– 3 and 8.64 × 10– 4 for the GRLW equation with different values of p. One can observe from Table 4 that the numerical results calculated with the present method are more accurate in comparison with Ref. [21].
| Table 4. Values of the error norms at different values of t and p for single soliton of the GRLW equation. |
The interaction of two GRLW solitary waves having different amplitudes and traveling in the same direction is illustrated. We consider the GRLW equation with the initial conditions given by the linear sum of two well separated solitary waves of various amplitudes
where

To allow the interaction to occur, the experiment was run from t = 0 to 10 and in the region – 150 ≤ x ≤ 100 for (p = 2, 4, 6, 8 with d1 = 1.005, d2 = 1.01, x1 = 40, x2 = – 30, h = 0.625, and k = 0.05. Errors in L2 and L∞ norms at several times are listed in Table 5 and compared with results in Ref. [21]. Figure 4 shows the interaction of two soliton solutions of the GRLW equation with p = 8. Throughout the simulation the L2 and L∞ error norms remain less than 1.6 × 10– 3 and 8.4 × 10– 4 for the GRLW equation with different values of p. A comparison with the method used in Ref. [21] shows that the error norms found with the present method are smaller than those obtained with that method.
| Table 5. Values of the error norms at different values of t and p for interaction of two solitary solutions of the GRLW equation. |
A numerical technique based on a collocation method using exponential B-splines has been presented for the numerical solution of the GRLW equation. The efficiency of the method is tested for the problems of propagation of the single solitary wave, interaction of two solitary waves, and development of an undular bore. The accuracy is examined in terms of the L∞ and L2 error norms and the conservation quantities 

| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|
| 66 |
|
| 67 |
|
| 68 |
|
| 69 |
|
| 70 |
|
| 71 |
|
| 72 |
|
| 73 |
|
| 74 |
|
| 75 |
|
| 76 |
|
| 77 |
|
| 78 |
|
| 79 |
|
| 80 |
|
| 81 |
|