†Corresponding author. E-mail: xytang@sist.ecnu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11275123, 11175092, 11475052, and 11435005), the Shanghai Knowledge Service Platform for Trustworthy Internet of Things, China (Grant No. ZF1213), and the Talent Fund and K CWong Magna Fund in Ningbo University, China.
The formal series symmetry approach (FSSA), a quite powerful and straightforward method to establish infinitely many generalized symmetries of classical integrable systems, has been successfully extended in the supersymmetric framework to explore series of infinitely many generalized symmetries for supersymmetric systems. Taking the 𝒩 = 1 supersymmetric Boiti–Leon–Manna–Pempinelli system as a concrete example, it is shown that the application of the extended FSSA to this supersymmetric system leads to a set of infinitely many generalized symmetries with an arbitrary function f ( t). Some interesting special cases of symmetry algebras are presented, including a limit case f ( t) = 1 related to the commutativity of higher order generalized symmetries.
Symmetry is an essential issue for nonlinear differential equations. However, compared with classical integrable systems, there is quite limited progress on symmetries of supersymmetric systems. As is known, many effective methods have been established to study various symmetries of classical nonlinear differential systems, for instance, the famous Lie group approaches[1, 2] and the direct method[3– 5] have been developed to study Lie point symmetries of partial differential equations. These methods can also be utilized to study symmetries of the SUSY equations. Recently, the classical Lie group approach has been used to find Lie symmetries, symmetry reductions and similarity solutions of the (2+ 1)-dimensional supersymmetric Boussinesq equation.[6] This approach has also been applied to the coupled bosonic system of the supersymmetric system obtained by the bosonization approach through introducing some fermionic parameters in the expansion of the superfield.[7] In addition, the nonlocal symmetry related to the Bä cklund transformation, also called residual symmetry, has been studied for the supersymmetric KdV equation and related interesting interacting wave solutions have been found.[8] Earlier symmetry related studies include the discrete symmetries of the 𝒩 = 2 supersymmetric modified nonlinear Schrö dingier (NLS) hierarchy[9] and the 𝒩 = 2 supersymmetric generalized NLS hierarchies, [10] the hidden symmetries of the 𝒩 = 4 supersymmetric Yang– Mills equations, [11] and the additional (non-isospectral) symmetries of the supersymmetric integrable hierarchies of Kadomtsev– Petviashvili type models.[12]
The formal series symmetry approach (FSSA) is famous for finding infinitely many generalized symmetries of integrable systems.[13, 14] It has been revealed that many famous (2+ 1)-dimensional physical models, such as the Kadomtsev– Petviashvili equation, [13] the Toda field equation, [14] dispersive long wave equations, [15] the Burgers system, [16] etc., admit one or more sequences of infinitely many generalized symmetries obtained by means of the FSSA. In this paper, taking an 𝒩 = 1 supersymmetric Boiti– Leon– Manna– Pempinelli system as an illustration, we for the first time intend to demonstrate that the FSSA can be extended in the supersymmetric framework to explore infinitely many generalized symmetries of supersymmetric systems.
The 𝒩 = 1 supersymmetric Boiti– Leon– Manna– Pempinelli (SUSY BLMP) system was given in a recent paper written by Delisle and Mosaddeghi[17]

where Di (i = x, y) denotes the supercovariant derivative defined as Di = ∂ θ + θ ∂ i. It is an 𝒩 = 1 extension of the classical BLMP equation[18]

obtained as usual by extending the space (x, y, t) to the superspace (x, y, t; θ ), where θ is a Grassmann variable satisfying θ 2 = 0. In addition, the bilinear form, multisolitons and bilinear Bä cklund transforms for the SUSY BLMP equation have been obtained.[17] It has also been pointed out that the BLMP equation is strongly related to the Korteweg-de Vries (KdV) equation, and naturally, the SUSY BLMP can be reduced to the SUSY KdV equation. The 𝒩 = 1 SUSY extension of the KdV equation was first formulated by Manin and Radul.[19] Similar to the role of the classical KdV equation in two-dimensional quantum gravity, [20, 21] it has been indicated that the 𝒩 = 1 SUSY extensions of the KdV equation might be relevant in the study of SUSY 2D quantum gravity.[22, 23] Such a significant role of the SUSY KdV equation has prompted ongoing theoretical investigations and a number of interesting properties have been established, for instance the bi-Hamiltonian structures, [24] the Painlevé property, [25] the Darboux transformation, [26] the Bä cklund transformation[27] and bilinear forms.[28, 29]
To apply the FSSA to the SUSY BLMP equation (1), let us first take the following finite Taylor expansion:

where ξ is a fermonic (odd) function and u is a bosonic (even) function, to transform the SUSY BLMP equation (1) into a system of two equations


It is evident that in the fermionic limit (ξ = 0), the above system is reduced to the classical BLMP equation (2). In Section 2, a set of infinitely many generalized symmetries of the SUSY BLMP system of Eqs. (4) and (5) is obtained. The related symmetry algebras in some interesting special cases are presented in Section 3. The last section is devoted to the summary and discussion.
A symmetry

of the SUSY BLMP system is defined as a solution of its linearized system by assuming that equations (4) and (5) are form invariant under the following infinitesimal transformation:

where ɛ is an infinitesimal parameter, Φ is a fermionic function, and U is a bosonic function. Substituting the infinitesimal transformation (7) into Eqs. (4) and (5) and picking up coefficients of ɛ arrive at the linearized equations that symmetries Φ and U should satisfy


Applying the formal series symmetry theory[13, 14] in the SUSY framework, we can expand symmetries Φ and U in the form of


respectively, where the fermionic function Φ n[k] and the bosonic function Un[k] are functions of x, y, u, ξ and their arbitrary derivatives, but not t dependent explicitly, f is an arbitrary function of t, and f(n− k) denotes the (n − k)-th derivative of f with respect to t.
The substitution of Eqs. (10) and (11) into Eqs. (8) and (9) leads to


Keeping the function f arbitrary requires the coefficients of different derivatives of f in the above two equations vanish identically. Therefore, by setting to zero all the coefficients of different derivatives of f, we obtain the following overdetermined equations:




for k = 2, 3, … , n + 1, and we have defined 
It is noted that Un[k − 1] and Vn[k] can be solved recursively from Eqs. (14)– (17) for a given g. The results can be expressed in the matrix form as

for k = 2, 3, … , n + 1, where the operators A and B are given by 

Similar to the classical case, the truncate conditions should be introduced so that meaningful generalized symmetries can be obtained, which are


Equivalently, Φ = Φ n[n] and U = Un[n + 1] satisfy the symmetry definition equations (8) and (9). Then in order to deduce explicit generalized symmetries, one has to fix an exact expression of the x-dependent function g in Eq. (18). Similarly, with the help of the dimensional analysis, one can find that the only possible selection of g is

Consequently, with this particular g given in Eq. (21), explicit generalized symmetries can be produced for the SUSY BLMP system of Eqs. (4) and (5). In principle, one can derive infinitely many generalized symmetries explicitly from the recursion equation, however, due to the difficulty in determining the integration functions, it is troublesome to write down explicit generalized symmetries for n > 2. Therefore, here we just present the first three explicit generalized symmetries, obtained by taking g = x/3, x2/18, and x3/162, respectively,


and

with

where the dot over the function denotes the derivative of the function with respect to t.
It is remarkable that in the derivation of symmetries (22)– (24), one can utilize the following tips to avoid the complicated computation caused by the anti-commuting fermionic functions. First, restrict the lower-order x-derivative of ξ placed in front of its higher orders, for instance, the term like ξ xxxξ x should be rewritten as − ξ xξ xxx. Second, to prove that the first one of the positive flow (taking f = 1 in σ 2(f)) also satisfies the symmetry definition equations (8) and (9), it is convenient to use the substitutions

where F1, F2, and F3 are all bosonic functions. Thus, σ 2(1) can be reformed as

with

With the substitution (25), equation (5) becomes

Hereafter, we mainly need to consider the anti-commuting relations involving the x-derivatives of the bosonic functions F1, F2, and F3, while other anti-commuting relations can be readily verified, when equations (26) and (27) are inserted into the symmetry definition equations (8) and (9).
The symmetries of the SUSY BLMP system can be given in a compact form by substituting Eq. (21) into Eqs. (10) and (11), that is
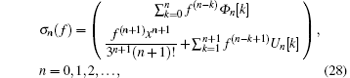
with

for k = 1, 2, … , n+ 1.
It is interesting to observe that the presence of the arbitrary function f in the generalized symmetries leads to a closed infinite-dimensional Lie algebra

Actually, it is not surprising that σ n(f) constitutes the algebra (30), because the symmetries of the classical BLMP equation constitute the same algebra. We also note that this algebra is isomorphic to those of the (2+ 1)-dimensional modified KdV type systems.[30, 31] Three interesting subalgebras of Eq. (30) are listed as follows.
Case 1f1 = f2 = 1. In this particular case, generalized symmetries with the presence of an arbitrary function f(t) degrade to t-independent symmetries

which constitute a commuting algebra

Such algebra implies the commutativity of the positive flow.
Case 2f = t. In this case, σ n(t) = τ n, called τ symmetries, linearly depend on the variables x, y, and t. The set of symmetries constitutes a centerless Virasoro algebra

It is well known that the Virasoro algebra of the asymptotic symmetry plays an important role in understanding the quantum nature of black holes.[32]
Case 3f = tr, and r ≠ 1 is an integer. In this case, we find that the general algebra reduces to w∞ type algebra

which contains all the conformal spins and plays a crucial role in some areas of physics, such as the sl(∞ ) Toda theory, [14, 33] integrable systems, [13, 34] membrane theory, [35]W string and W gravity theories.
In this paper, we have demonstrated that the 𝒩 = 1 SUSY BLMP equation admits a set of infinitely many generalized symmetries with an arbitrary function f(t). It has also been shown that these symmetries constitute a closed infinite-dimensional Lie algebra which is a generalization of the w∞ type algebra. Thus we conclude that the SUSY BLMP equation is integrable in the sense of symmetry.
In addition, one can obtain in a similar way that the SUSY BLMP equation also admits a special simple symmetry with an arbitrary function p = p(y),

which is commuting with the generalized symmetries σ n(f) by

Furthermore, from Eqs. (22), (23), and (35), one can find the SUSY BLMP possesses the following infinite-dimensional Lie point symmetries of the form

where f and h are arbitrary functions of t, and p is an arbitrary function of y. In such a special selection, it is effortless to check that the nonzero commutation relations of these symmetries are



which constitute an infinite-dimensional Kac– Moody– Virasoro– type algebra.
The additional properties of the SUSY BLMP equation, and what we know about the SUSY extensions of (2+ 1)-dimensional classical integrable systems are worthy of further study. As mentioned above, it has been confirmed that the equations of motions and symmetries in the quantum 2D gravity and the noncritical string theory at least c < 1 can be formulated in the KdV type equations.[20, 21] Similarly, it has also been indicated that the 𝒩 = 1 supersymmetric extensions of the KdV equation might be relevant in the study of the supersymmetric 2D quantum gravity.[22, 23] In the viewpoint of physics, the (2+ 1)-dimensional field theory is particularly interesting since the theory is simple yet possesses a rich asymptotic symmetry and provides us with a deeper insight in general.[36] Consequently, it is significant to study supersymmetric extensions of the KdV equation, especially those in 2+ 1 dimensions.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|


