In the past decades, many kinds of neural networks, such as cellular neural networks, Hopfield neural networks, Cohen– Grossberg neural networks, recurrent neural networks (RNNs), complex dynamical networks (CDNs), bidirectional associative memory (BAM) neural networks, chaotic neural networks (CNNs), and static neural networks (SNNs), have been studied because they have extensive applications in different fields such as fault diagnosis, pattern recognition, signal processing, and parallel computation.^{[1– 4]} Some of these applications require the equilibrium points of the designed networks to be stable. Since axonal signal transmission delays often occur in various neural networks, and may also cause undesirable dynamic network behaviors such as oscillation and instability, it is important to study the stability of the neural networks.^{[5– 8]}

Considerable efforts have been dedicated to the stability analysis of neural networks with delays. Most neural networks can be classified as either continuous^{[9, 10]} or discrete.^{[11, 12]} While, the signal propagation is sometimes instantaneous and can be modeled with discrete delays, it may also be distributed during a certain time period so that distributed delays are incorporated into the model.^{[13– 15]} Therefore, both discrete and time-varying distributed delays should be taken into account when modeling a realistic neural network.

On the other hand, a neural network is a highly interconnected network with a large number of neurons, and as a result most neural networks are large-scale and complex networks. In fact, only partial information about the neuron states is available in the outputs of large-scale neural networks. It is very difficult to obtain the state estimation of the neurons in neural networks because the neural networks have complicated structures. Therefore, it is important to estimate the neuron states through available measurement outputs, and there are many remarkable attempts to design state estimators for various types of neural networks.^{[16, 17]} The delay-dependent H_∞ problems for delayed neural networks have received substantial attention from the control community for the past few years.^{[18, 19]} The H_∞ control of switched neutral-type neural networks was presented in Ref.  [20] to estimate the robust exponential stability. However, to the best of the authors’ knowledge, the H_∞ state estimation of static neural networks with discrete and distributed time-varying delays via augmented Lyapunov approach has not yet been considered, which motivates this study.

In this paper, we study the delay-dependent H_∞ state estimation problem for a class of neural networks with discrete and distributed time-varying delays. Our main aim is to design a delay-dependent state estimation gain matrix, such that the concerned system is globally asymptotically stable with a prescribed H_∞ performance of disturbance attenuation for all admissible parameters. A sufficient condition for the H_∞ state estimation is presented in terms of linear matrix inequality (LMI) using the augmented Lyapunov– Krasovskii functional (LKF) together with the zero function which guarantees the global asymptotic stability of the concerned neural networks. Finally, numerical examples are given to illustrate the usefulness and effectiveness of the proposed method.

The following notations are used. Throughout this paper, ℛ ⁿ and ℛ ^{n× n} denote, respectively, the n-dimensional Euclidean space and the set of all n × n real matrices. The notation * represents the entries implied by symmetry. The matrix transpose and inverse of A are denoted as A^T and A^{− 1}, respectively. The X > 0 means that matrix X is real symmetric positive definite with appropriate dimensions. The I denotes the identity matrix with appropriate dimensions. Let , where ‖ f ‖ refers to the Euclidean norm of the functionf(t) at time t, and L₂[0, ∞ ) is the space of square integrable vectors on [0, ∞ ).

Consider the following neural network with discrete and distributed time-varying delays:

where x(t) = [x₁(t), x₂(t), … , x_n(t)]^T ∈ ℛ ⁿ is the state vector of the network at time t ≥ 0, n is the number of neurons, y(t) ∈ ℛ ^m is the network measurement, z(t) ∈ ℛ ^q, to be estimated, is a linear combination of the states, and w(t) ∈ ℛ ^p is the noise input belonging to L₂[0, ∞ ). Here A = diag{a₁, … , a_n} is a diagonal matrix with a_i > 0, i = 1, 2, … , n; B, W₀, and W₁ represent the connection weight matrix, the discretely delayed connection weight matrix, and the distributively delayed connection weight matrix, respectively; and, C, D, B₁, B₂, and H are known real constant matrices with appropriate dimensions. The g(x(t)) = [g(x₁(t)), … , g(x_n(t))]^T ∈ ℛ ⁿ denotes the neuron activation function at time t, and J = [J₁, … , J_n]^T∈ ℛ ⁿ is a constant external input vector. The ϕ (t) is the initial condition. The τ (t) and d(t) denote the discrete time-varying and distributed time-varying delays, respectively, and are assumed to satisfy

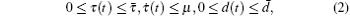
where , μ , and are constants.

Assumption 1 Each neuron activation function g_i(t), (i = 1, 2, … , n) is continuous and bounded, and satisfies the following condition:

with are some constants and k₁, k₂∈ ℛ , k₁≠ k₂

We consider the following state estimator for the neural network  (1):

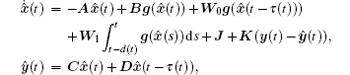
where denotes the estimated state, , denotes the estimated measurements of y(t), z(t), respectively, and K is the estimator gain matrix to be determined.

Define the error ) and . Then, based on Eqs.  (1) and (4), we easily obtain the error system as follows:

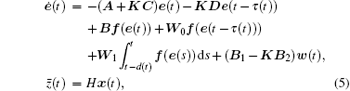
where e(t) = [e₁(t), e₂(t), … , e_n(t)]^T ∈ ℛ ⁿ is the state vector of the transformed system and . It follows from Assumption 1 that the neural activation function satisfies

where k ∈ ℛ , k ≠ 0.

Definition 1 Given a prescribed level of noise attenuation γ > 0, the error system  (5) is said to be globally asymptotically stable with a prescribed level of noise attenuation γ , if there is a proper state estimator  (4) such that the equilibrium point of the result error system  (5) with w(t) = 0 is globally asymptotically stable, and under zero-initial conditions for all nonzero w(t) ∈ L₂ [0, ∞ ).

Lemma 1 (Schur complement^[21]) Let M, P, Q be given matrices such that Q > 0, then

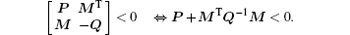
Lemma 2^[22] For any constant matrix M ∈ ℛ ^{n× n}, M = M^T > 0, scalar η > 0, vector function w : [0, η ] → Rⁿ such that the integrations concerned are well defined, we have

Lemma 3^[23] For real matrices P > 0, M_i (i = 1, 2, 3) with appropriate dimensions, and τ (t) satisfying Eq.  (2), we have

where

Lemma 4^[24] For any scalar τ (t) ≥ 0 and any constant matrix Q ∈ ℜ ^{n× n}, Q = Q^T > 0, the following inequality holds:

where ξ (t) is defined in Lemma 3 and V is a free-weighting matrix with appropriate dimensions.

Lemma 5^[25] The inequalities

are equivalent to the following condition:

where R₁, R₂, and Δ are constant matrices with appropriate dimensions, variable m ∈ [0, β ] ∈ ℛ , and β > 0.

Theorem 1 For given scalars and matrix K, the error system  (5) is globally asymptotically stable with H_∞ performance γ if there exist real matrices P > 0, P₁₁ > 0, P₁₂, P₂₂ > 0, Q₁ > 0, Q₂, Q₃ > 0, R > 0, S > 0, T₁ > 0, T₂ > 0, Z₁ > 0, Z₂, Z₃ > 0, T > 0, and any appropriate dimensions matrices M_l, N_l, U_m, V_m, (l = 1, 2, … , 6, m = 1, 2), such that the following LMIs hold:

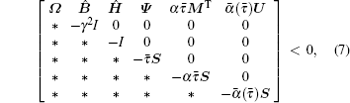
where

with

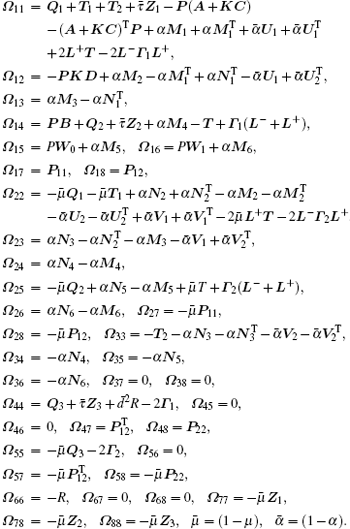
Proof Define the Lyapunov functional candidate as follows:

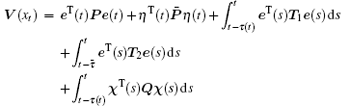
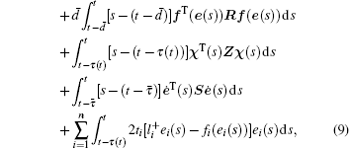
where

By calculating the time derivative of V(x_t), we obtain

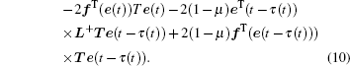
By using Lemma 2, we obtain

From LMI  (10), we have

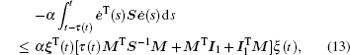
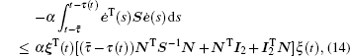
where By using Lemma 3, we obtain

where

By using Lemma 4, we have

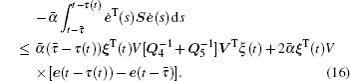
In addition, for positive diagonal matrices Γ ₁ > 0, Γ ₂ > 0, the following equations hold based on formula  (6):

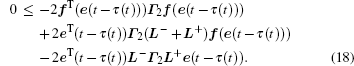
By combining inequality  (10) to inequality  (18), we obtain

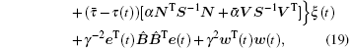
where the inequality

is used, ζ (t) is defined by and Ω is defined the same as in LMI  (7). Under the zero initial conditions and V(x_t)| _{t= ∞} → 0 for system  (1), we have

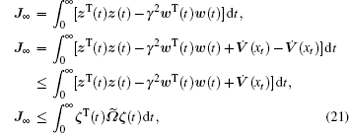
where

Obviously, if then Based on Lemma 5, the matrix inequality is equivalent to the following matrix inequalities:

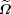
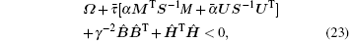
when and τ (t) → 0, respectively. By applying Schur complement lemma to inequalities  (23) and (24), we obtain LMIs  (7) and (8), respectively. Now it is easy to see that for any nonzero w(t) ∈ L₂[0, ∞ ) is satisfied. When w(t) ≡ 0, the error system  (5) is globally asymptotically stable.

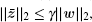
In this section, we present a delay-dependent sufficient condition for the solvability of the H_∞ performance of the concerned neural network.

Theorem 2 Consider the neural network  (1) and let γ > 0 be a prescribed scalar. The H_∞ state estimation problem is solvable if there exist matrices P > 0, P₁₁ > 0, P₁₂, P₂₂ > 0, Q₁ > 0, Q₂, Q₃ > 0, R > 0, S > 0, T₁ > 0, T₂ > 0, Z₁ > 0, Z₂, Z₃ > 0, T > 0, and any appropriate dimensions matrices M_l, N_l, U_m, V_m, (l = 1, 2, … , 6, m = 1, 2), such that the following LMIs hold:

where

with

Proof Define K = P^{− 1}G, then pre and post multiplying LMIs  (7) and (8) by diag and diag respectively. By using the inequality (see Ref.  [26]) we obtain LMIs  (25) and (26). This completes the proof.

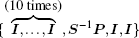
Remark 1 In order to show the reduced conservatism of our stability criteria, we consider the following systems as a special case of the system  (1) reduced to a neural network with time-varying delays described by

Using the same method in Theorem 1, we can obtain the following results.

Corollary 1 For given scalars and matrix K, the neural network  (27) is globally asymptotically stable with H_∞ performance γ if there exist real matrices P > 0, P₁₁ > 0, P₁₂, P₂₂ > 0, Q₁ > 0, Q₂, Q₃ > 0, R > 0, S > 0, T₁ > 0, T₂ > 0, Z₁ > 0, Z₂, Z₃ > 0, T > 0, and any appropriate dimensions matrices M_l, N_l, U_m, V_m, (l = 1, 2, … , 6, m = 1, 2), such that the following LMIs hold:

where

with

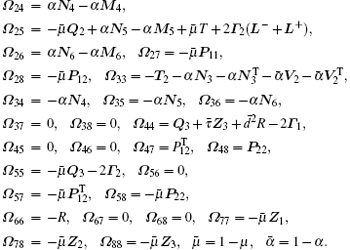
Remark 2 Recently, the H_∞ state estimation of static neural networks with time-varying delays was studied in Ref.  [27]. Furthermore, the delay-dependent H_∞ state estimation of neural networks with discrete and distributed delays was investigated in Ref.  [28]. The H_∞ cluster synchronization and state estimation for delayed complex dynamical networks were presented in Ref.  [29]. In Theorem 2, we present a sufficient condition to ensure that the error system  (5) is globally asymptotically stable with an H_∞ performance index γ > 0. The delay-dependent condition is derived by constructing an augmented Lyapunov– Krasovskii functional with Lemmas 3 and 4.

Example 1 Consider the neural network  (27) with the following matrix parameters:

By solving LMI in Corollary 1 with , α = 0.5, and μ = 0.3, and using LMI toolbox, ^[30] the feasible solutions are

Example 2 Consider the neural network  (1) with the following matrix parameters:

By solving LMI in Theorem 2 with d = 0.5, μ = 0.5, and α = 0.3, and using the LMI toolbox, the feasible solutions are

The state estimator gain matrix is then obtained as

The minimum H_∞ performance index γ with different and fixed d = 0.5 and μ = 0 is listed in Table  1.

Table 1.

Table 1.

Table 1. Minimum H∞ performance index γ with different (, μ ) and fixed d = 0.5 and μ = 0 for Example 2. Method α (1, 0.3) (0.9, 0.5) (0.9, 0.3) (0.8, 0.5) (0.8, 0.3) γ in Ref.  [28] 0.15 1.3784 1.3475 1.3148 1.2846 1.2451 γ in Thm 2 1.2086 1.1807 1.1649 1.1456 1.1278 γ in Ref.  [28] 0.25 1.3278 1.2973 1.2611 1.2314 1.1952 γ in Thm 2 1.1797 1.1584 1.1337 1.1151 1.0952

Table 1. Minimum H∞ performance index γ with different (, μ ) and fixed d = 0.5 and μ = 0 for Example 2.

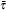Example 3 Consider the neural network  (1) with the following matrix parameters:

Table 2.

Table 2.

Table 2. Minimum H∞ performance index γ with different (,   μ ) and fixed d = 0.5 for Example 3. Method (0.9, 0.3) (1, 0.5) (1, 0.4) (1, 0.3) α = 0.5 0.6830 0.8207 1.0349 1.1456 α = 0.7 0.6776 0.8017 1.0237 1.1351

Table 2. Minimum H∞ performance index γ with different (,   μ ) and fixed d = 0.5 for Example 3.

By solving LMI in Theorem 2 with 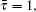, d = 0.5, μ = 0.5, and α = 0.5, and using the LMI toolbox, the state estimator gain matrix is obtained as

The result is presented in Table  2.

In this work, we have studied the H_∞ state estimation control of neural networks with discrete and distributed time-varying delays. Some improved delay-dependent H_∞ state estimation analyses have been established in terms of linear matrix inequality by constructing an appropriate type of LKF for delayed neural networks. It is shown that a desired state estimation controller gain matrix can be constructed when the given linear matrix inequalities are feasible. Numerical examples are given to demonstrate the effectiveness and the usefulness of the proposed method. The results are also compared with existing methods. In this paper, we have considered augmented LKFs to show the less conservative results. However, we construct the augmented LKFs with single integral terms. We would like to point out that it is possible to extend our main results to a more general discrete-time uncertain neutral with interval time-varying and distributed delays by using the augmented LKF approach with triple integral terms. The results will appear in the near future.