†Corresponding author. E-mail: karpov@iph.krasn.ru
*Project supported by the Russian Academy of Sciences (Grant Nos. 24.29, 24.31, III.9.5, 43, SB RAS-SFU (101), and 3-9-5).
Interactions of pulsed laser radiation with resonance domains of multiparticle colloidal aggregates having an increasingly complex local environment are studied via an optodynamic model. The model is applied to the simplest configurations, such as single particles, dimers, and trimers consisting of mono- and polydisperse Ag nanoparticles. We analyze how the local environment and the associated local field enhancement by surrounding particles affect the optodynamic processes in domains, including their photomodification and optical properties.
The physics of interactions between metallic nanoparticle aggregates and pulsed laser radiation is an important part of nanoplasmonics; it involves a broad scope of research in optics and nonlinear optics accompanied by a wide range of application problems.[1– 20] In particular, these problems involve fabrication of surface plasmon polariton waveguides and devices, novel solutions in medicine, lab-on-a-chip plasmonic biosensing, plasmonic enhancement of optical properties of metal nanoparticles and ultrasensitive Raman spectroscopy of biomolecules adsorbed by plasmonic nanoparticles in colloidal aggregates, new nonlinear optical and photochromic composite materials containing plasmonic colloidal aggregates, and so forth.
Approaching most of the problems requires a deep understanding of the processes underlying the interaction of high intensity optical radiation with systems of plasmonic nanoparticles.
Under external optical radiation, plasmonic nanoparticle aggregates feature giant fluctuations of electromagnetic field that are strongly associated with the geometry of the local environment of each particle or, more exactly, with the degree of anisotropy of the local environment of particles in an aggregate.[21, 22]
Fluctuations of electromagnetic field, in turn, result in inhomogeneous broadening of plasmon absorption bands of disordered multiparticle aggregates. The absorption amplitude at the resonance frequency correlates with the number of resonance domains.[3, 4, 23]
Resonance domains can include both single particles and groups of particles in an aggregate with a single resonant frequency closely coupled by electromagnetic interaction.[17, 21, 22, 24] Their location in an aggregate is determined by the maximum amplitude of the local field.
Generally speaking, the resonance domain is a group of closely spaced optically interacting particles in an aggregate whose resonance frequency coincides with or is close to the radiation frequency. In our case, proximity of a particle to resonance is determined by the maximum magnitude of dipole moments induced by laser radiation.
Electromagnetic interaction of particles with each other in a resonance domain and with an applied optical field may alter the resonance frequencies, depending on the position of particles in the domain and the particle size.[3, 4, 16, 21, 22, 24] The inhomogeneously broadened extinction spectrum of a multiparticle aggregate is a set of spectral modes spread over a wide range of frequencies corresponding to different resonance domains.[3, 4, 23]
Optical interparticle links[25] are realized due to the dipole interaction between particles; the dipole moment of each of them is calculated by the coupled dipole method (see, e.g., Refs. [3], [4], and [16] and references in Ref. [17]) allowing for the contribution from higher multipoles.[23, 26] In Ref. [24], we reported finding the roles and contributions of various interrelated factors leading to photomodification of Ag dimer-type domains under applied picosecond laser pulses. Evolution of the spectral properties of a domain, whose resonance frequency dynamically changes while a picosecond laser pulse is on, may be associated with changes in the aggregate state of the metallic core of particles in domains, and after the pulse is over with shifts of neighboring particles in the domain relative to each other. Furthermore, the spectral properties of a domain may vary with the sizes[26] and shapes of the particles (see also our earlier paper[16] covering the effect of particle polydispersity on the dimer absorption spectrum). All these processes lead to photomodification of the resonance domain and, hence, to photomodification of large colloidal aggregates in pulsed laser fields. This causes photochromic reactions in noble metal nanocolloids and nanocomposite plasmonic materials. Note also that understanding the processes in resonance domains in pulsed laser fields can help to explain the pattern of interaction of multiparticle colloidal aggregates with laser radiation in various optical and nonlinear optical phenomena.
Our aim is to study the interaction between pulsed laser radiation and a resonance domain of a multiparticle aggregate depending on the number of particles in the domain and to find out how the local environment of plasmonic nanoparticles affects any photomodification and the kinetic characteristics of the domain.
The model of resonant interaction of a domain with laser pulses proposed in Ref. [24] takes into account a wide range of interrelated mechanical, thermodynamic, chemical, physical, and optical processes. On one hand, these processes are due to the local interparticle interactions, of various natures, occurring in domains of a multiparticle aggregate, and on the other hand, they arise from factors accompanying these interactions. Note that models of the resonant interaction of a domain with laser radiation were also considered in Refs. [14]– [16].
The physical pattern of the interaction of a domain with laser radiation is as follows. Before a laser pulse is applied, there is a balance of the van der Waals and elastic forces in the domain particles. High-intensity laser radiation generates light-induced forces, existing however only for as long as the pulse is on. Absorption of radiation by the domain leads to heating of conduction electrons in the particles. Heating of electrons leads to heating of the ionic subsystem of the particle material (crystal lattice) and the heat is transferred to the polymer adsorption layer (adlayer). This results in the destruction of molecular bonds in adlayers and the degradation of their elastic properties. This is accompanied by an imbalance of forces and by approaches of particles to each other under the van der Waals attraction (up to a complete contact of their metallic surfaces). Furthermore, heating and melting of particles results in increased relaxation constants of conduction electrons, which reduces the Q-factor of surface plasmon resonance and hence affects the efficiency of laser interaction with the domain. That is, radiation affects the position of a particle in the domain through their heating and thereby changes the optical properties of particles (in case of melting) as well as changing the elastic properties of their adlayers. Thus, interaction of a nanoparticle aggregate with radiation is essentially nonlinear. Note that the role of melting was ignored in the earlier models of resonant domains (see, e.g., Refs. [17] and [18]).
Our model is based on the system of differential equations and the set of linear algebraic equations (18) from Ref. [24]
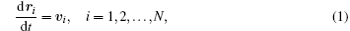
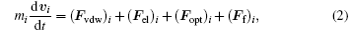
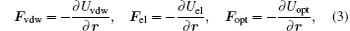

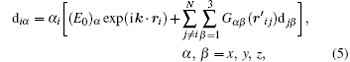

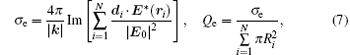
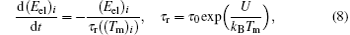

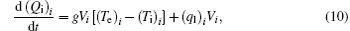
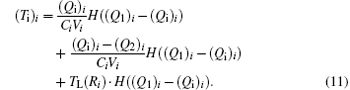
Here t is the time from the start of the pulse; mi, Ri, υ i, ri, and Fi are the mass, radius, speed, and radius vector of the center of mass of the i-th particle, and the resultant force; (Fvdw)i is the van der Waals force, (Fel)i is the elastic force related to the deformation of the adlayers of contacting particles; (Fopt)i is the optical force caused by the interaction of light-induced dipoles; (Fv)i is the viscous friction force; (Ff)i is the tangential interparticle friction forces; Uopt is the potential energy of the interaction of light-induced dipole moments; di is the light-induced dipole moment; E(r) is the strength of external electromagnetic field (E0 is the amplitude of the field, and the symbol (* ) denotes complex conjugation); α i is the dipole polarizability of the i-th particle; τ is the laser pulse duration; H(x) is the Heaviside function; k is the wave vector of laser radiation; r′ ij is the vector joining the centers of the particles, adjusted for the renormalization coefficient; [26]Gα β is the interparticle interaction tensor; [25]ε i is the dielectric constant of the particle taking into consideration its size, temperature, and aggregate state; ε m is the dielectric constant of the interparticle medium; σ e is the extinction cross section, Qe is the extinction efficiency, (Eel)i is the elasticity modulus of particle adlayer; τ 0 = 10− 12 s– 10− 13 s is the characteristic vibration period of atoms in molecules. τ r is the relaxation time of molecular bonds in adlayers; (Tm)i is the average temperature of the heated area near the i-th particle; (Te)i, (Ti)i are the temperatures of electron and lattice (ion) component of the i-th particle; (Ce)i is the volumetric heat capacity of electron components; g is the rate of energy exchange between the electron and ion subsystems; Wi is the absorbed power of laser radiation; Vi is the particle volume; ω is the angular frequency of the laser radiation; (ql)i is the heat flow per unit volume, describing thermal losses; TL(Ri) is the size dependence of the melting temperature; (Qi)i is the thermal energy transferred to the ion component of a particle, (Q1)i, and (Q2)i are the thermal energies at the initial and final stages of melting. Greek subscripts denote the Cartesian components of vectors and tensors.
Unlike the original version, [17, 18] the model in Ref. [24] takes into account the following factors: the light-induced interparticle forces in aggregates with an arbitrary geometry and an arbitrary number of particles; the polydispersity of particles inherent in real metallic nanocolloids; the dependence of the metal relaxation constant on the temperature and aggregate state of the particle material, and the melting temperature dependence on the size of the particle. As shown below, the multifactorial nature of the interaction of a domain with laser radiation leads to complex dynamics of particles in domains depending on the radiation parameters. Allowance for the accompanying phenomena related to interaction that play a key role in laser photomodification of plasmonic nanoparticle aggregates makes the model versatile and suitable for describing real optical and nonlinear optical processes occurring in arbitrary nanocolloids and “ metal-insulator” nanocomposites.
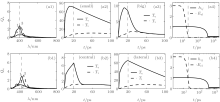
In this section we discuss the results of applying our optodynamic model to calculate the kinetic characteristics of the interaction between pulsed laser radiation and resonance domains of a multiparticle colloid aggregate such as a trimer consisting of three spherical Ag nanoparticles with different local environments (Figs. 1(a), 1(b)). In addition, we compare these results with the kinetic characteristics of dimers as well as with single spherical Ag particles without regard to the local environment (Fig. 1(a)). Thus we have a set of objects with different local environments, which brings out the contribution of this factor to the investigated processes. In a general case, orientation of dimers to the laser field polarization can be arbitrary. In this section, however, we chose to study resonant domains that are parallel to the polarization (Fig. 1(b)), since in this case the photomodification effects (changes of spectral and structural characteristics) are most pronounced (compared to the transversal polarization). The domain characteristics were shown to change insignificantly for transverse polarization under the same conditions.
We emphasize that the locally anisotropic environment of particles in colloidal aggregates (i.e., their chain-like structure) is their intrinsic feature, so the trimers in a triangular configuration are atypical in disordered aggregates with a dendrite structure (see, e.g., Refs. [21], [22], and [27]).
In typical nanocolloids, nanoparticle diameters fall within the range 3 nm– 20 nm. In this paper we demonstrate the difference between the interactions of laser radiation with domains formed by monodisperse and polydisperse nanoparticles. In the monodisperse case, the particle radii are 5 nm. In the case of polydisperse particles, the radius is Ri = 8 nm for a bigger particle (B) and Ri = 2 nm for a smaller one (S). (The average size is 5 nm, as in the monodisperse case.)
We compare the basic kinetic characteristics of monodisperse and polydisperse resonant trimers with those of the corresponding dimers (for the latter we look at the “ resonance case” ; i.e. when the peak of the extinction spectrum (within the plasmon absorption band) λ max occurs at the laser radiation wavelength λ las), the average radius of a polydisperse domain being the same as the radii of monodisperse particles. The following domain characteristics (see Fig. 2) are compared: the extinction spectra Qe(λ ), the temperature of ion (Ti)i and electron (Te)i components of the metal, the interparticle gap hij and the elasticity modulus (Eel)i of the polymer adlayer of particles. Changes in the domain characteristics due to heating and melting of the particle material occur under applied laser pulses having τ = 20 ps duration and various wavelengths.
The initial values are hij ≈ 1 nm for the interparticle gap, hi = hj = 0.65 nm and Eel = 3 × 108 N/m2 for the thickness and the elasticity modulus of the polymer adlayer, respectively (hij < hi + hj in the case of the deformation of adlayers in the contact area). The elasticity modulus depends on the balance of particles in the domain before a laser pulse is applied.
Figure 1(a) illustrates the evolution of the extinction spectrum Qe, (Fig. 1(a): (a1), (a3), (a5); curve 1) and the temperature of the electronic Te and the ionic Ti subsystems (Fig. 1(a): (a2), (a4), (a6)) of a single spherical particle with radius Ri = 5 nm under the action of a picosecond laser pulse. The radiation intensity in Fig. 1#cod#x02013; 3 is I = 7.5 · 108 W/cm2, which corresponds to the lower threshold of manifestations[24] of static (persistent after the pulse) photomodification of a monodisperse resonant domain (dimer or trimer). The extinction spectrum of a low-concentration aggregated colloid within the plasmonic absorption band virtually coincides with the absorption spectrum because the absorption is a dominant factor in extinction (scattering is negligible). Changes in the extinction spectrum of a single particle caused by a picosecond laser pulse are manifested by a drastic decrease in the Q-factor of the plasmon resonance (Fig. 1(a): (a1), (a3), and (a5); curve 2). This is due to the increased relaxation constants of heated particles when they reach the melting temperature (Fig. 1(a): (a2), (a4), (a6)).[24] The original plasmon resonance recovers as the single particle cools down 300 ps– 400 ps after the laser pulse ends.
Figure 2 shows the kinetics of the basic characteristics (see above) of monodisperse domains consisting of two (Fig. 2(a)) and three (Fig. 2(b)) particles with a radius Ri = 5 nm. Figure 2(b) illustrates the kinetics of the elasticity modulus (Eel)i for the central particle, since the change of (Eel)i for lateral particles is negligible.
A distinctive feature of the extinction spectrum of a trimer compared to that of a dimer is a greater extension of its long-wavelength wing (Fig. 2(a), and, Fig. 2(b): (b1)). This is explained by the stronger electromagnetic interactions between particles in a trimer leading to the shift of eigen resonances of particles.
The local field enhancement effect has a different impact on the process of photomodification of a monodisperse trimer compared to a monodisperse dimer. The difference lies in the heating rate of the central and lateral particles (Fig. 2(b): (b2), and (b3)). A significant difference between temperatures of particles in a trimer is due to the different local environments of the particles. In particular, the central particle in a trimer is surrounded by two lateral particles, while particles in a dimer each have just one adjacent particle. The presence of lateral particles in a trimer increases the local field near the central particle due to the fields produced by light-induced dipole moments of the neighboring particles. The local field near the center of a trimer is stronger than the local fields near lateral particles, and stronger than that around each of the particles in a dimer (for the same particle size and interparticle gaps). This explains why the electron and ion subsystems reach their maximum temperatures near the central particle. In particular, in the case of resonance (Fig. 2(b)), because of heating of the central particle in the trimer (Fig. 2(b): (b2)) the elasticity modulus of its adlayer reduces and the particles approach each other under the influence of the van der Waals forces (Fig. 2(b): (b4)). Thus, prevalent heating of central particles in a monodisperse trimer is the dominant factor in its photomodification.
If domain particles reach the melting temperature while the laser pulse is on, there is a sharp decrease in the quality factor of plasmon resonances (Fig. 2(a): (a1); Fig. 2(b): (b1); curve 2), describing the dynamic photomodification (manifested only during the pulse).
Once the pulse ends, spectral changes are caused by the approach of particles to each other, which is due to the low elasticity modulus of adlayers and the predominant influence of the van der Waals attraction. The approach leads to a shift of the extinction spectrum to the long-wavelength range (Fig. 2(a): (a1); Fig. 2(b): (b1); curve 3). Cooling of the particle restores its plasmon resonance.
The irreversible approach of particles to each other contributes to static changes[24] both in optical and in structural characteristics.
As noted above, the local environment is determined not only by locations of neighboring particles in a domain but also by their size. Even if particles are arranged symmetrically with respect to the central particle, if their size is different, the local field enhanced by adjacent particles and acting on the central particle is determined by the size of the surrounding particles as well.
Figure 3 shows the kinetics of the basic characteristics of a polydisperse domain consisting of two (Fig. 3(a)) or three (Fig. 3(b)) different size particles: big Ri = 8 nm (B) and small Rj = 2 nm (S). Kinetics of the elasticity modulus is given for small particles (for larger ones it varies insignificantly).
The extinction spectrum of a polydisperse domain exhibits asymmetry of the plasmon absorption band (Fig. 3(a): (a1); Fig. 3(b): (b1); curve 1 (see also Ref. [24])). Note that the spectrum of polydisperse domains is less extended into the long-wavelength range than monodisperse domains, due to the weaker electromagnetic interaction of highly polydisperse particles.
The effect of the difference in the local field of nearby particles is even more pronounced among polydisperse trimers than among monodisperse trimers, because the local environment is not only determined by the position but also by the size of neighboring particles.
To study the photomodification of polydisperse trimers, we used a “ small-big-small” — SBS (rather than BSB) configuration, since the high local field enhanced by big lateral particles on a small central particle in a BSB configuration leads to instantaneous melting of small particles. Under these conditions, the BSB domain spectrum is similar to that of two separate weakly interacting particles.
The different heating rates and temperatures of the particles (Fig. 3(a): (a2), (a3); Fig. 3(b): (b2) and (b3)) are explained by a different-size environment wherein a bigger central particle produces a higher local field near small lateral particles. While a small particle melts upon reaching the melting temperature under the applied pulse and loses its resonant properties, a bigger particle maintains its crystal lattice. This leads to a shift of the extinction spectrum maximum to the short-wavelength range. Melting of bigger particles is accompanied by a sharp decrease in the quality factor of the plasmon resonance (Fig. 3(b): (b1); curve 2). The effects described above correspond to a manifestation of dynamic photomodification.
Changes in the extinction spectrum (Fig. 3(b): (b1); curve 3) and structural characteristics (Fig. 3(b): (b4)) 20 ns after the pulse ends are the result of static photomodification.
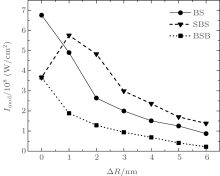
Figure 4 is a generalized dependence of the threshold of static photomodification of the domain as a function of nanoparticle size dispersion Δ R. As can be seen from the figure, for the dimer (BS) and trimer (BSB) configurations, the photomodification threshold monotonically decreases with growing Δ R, whereas for SBS trimers, this dependence is nonmonotonic.
Since static photomodification occurs when the elasticity modulus of the adlayer of at least one particle drops far enough to allow the collapse of the domain under the van der Waals attraction, the threshold of photomodification of this type of domain is determined by the temperature of the hottest particles. The temperature of a particle is determined by its local environment, and hence by the local electromagnetic field produced by this environment. In a dimer, the hottest particle is always the smaller one, [24] since a bigger particle produces stronger local field on the smaller one. Accordingly, a growing difference in the particle size results in higher temperatures of small particles and eventually in a lower photomodification threshold. Similarly, in the BSB trimer, two big particles surrounding a small central particle produce a stronger local field than the small particle does on big ones. This requires less laser field energy for photomodification with increased size dispersion.
However, the situation is different in an SBS trimer. When the size dispersion is insignificant, the local field enhanced by two small particles surrounding a bigger one is stronger than the local field enhanced by the big particle on small ones. Static photomodification in this case is determined by the energy expended on melting of the big central particle. Thus the local field enhanced by smaller particles on bigger ones decreases with the growth of the size dispersion Δ R, increasing the threshold for small Δ R (Δ R < 1 nm). However, beyond a certain value of Δ R (Δ R > 1 nm), when the size dispersion is significant, the local field enhanced by bigger particles on smaller ones becomes stronger than the field enhanced by smaller particles on the bigger ones. Once this becomes the case, static photomodification will be determined by the temperature of the small particles. Since the local field at small particles increases with Δ R, the photomodification threshold decreases.
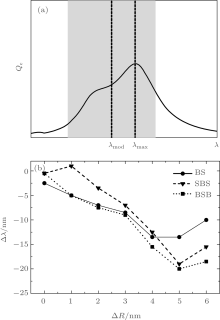
Figure 5(a) schematically illustrates the range of laser radiation wavelengths against the extinction spectrum of domains and its maximum (λ max), within which static photomodification of polydisperse domain is possible. There are two resonances of the system in the extinction curve: short-wavelength (weakly pronounced) and long-wavelength resonances (the latter has a higher amplitude). As Δ R grows, the short-wavelength resonance shifts toward shorter wavelengths and reduces its amplitude.
Figure 5(b) shows the dependence of the shift of the spectral range of domain photomodification (λ mod – λ max = Δ λ ) on Δ R. The calculations are performed for a field strength 1.15 times greater than the threshold of photomodification at the laser wavelength λ las = λ max (τ = 20 ps). As can be seen from Fig. 5(b), as Δ R grows, the middle of the photomodification range (λ mod) monotonically shifts to shorter wavelengths relative to λ max. This feature was found statistically in the calculations of photomodification for a large series of dimers and trimers and various Δ R values.
As can be seen from the presented dependence, the shift of the photomodification range toward shorter wavelengths increases with the degree of polydispersity of the domain. This is explained by the asymmetry of the absorption band of a polydisperse domain having a longer short-wavelength wing, which contributes to a stronger absorption of radiation in this wing. In a monodisperse domain, the range shift tends to zero, due to the symmetry of the extinction contour.
Slight nonmonotonicity in the dependence Δ λ (Δ R) (Fig. 5(b)) is observed as it increases at Δ R = 6 nm, due to a decrease of the amplitude of short-wavelength resonance of the system and shortening of the short-wavelength wing with growing Δ R. Accordingly, the shortening leads to a reduced radiation absorption in the short-wavelength wing. Thus, for Δ R = 6 nm, the chosen laser intensity appears to be insufficient
for static photomodification. In this case, absorption occurs in the range of longer wavelengths, and the range of photomodification shifts to the same range. In a monodisperse domain, the shift tends to zero due to the symmetry of the extinction contour.
The spectral range of static photomodification of a resonance domain of a multiparticle colloidal aggregate under picosecond pulsed laser fields shifts to a short-wavelength range relative to the maximum of the domain absorption band with the growing size dispersion.
A higher degree of polydispersity of the resonance domain reduces the radiation intensity threshold of its static photomodification. Since static photomodification occurs when the elasticity modulus of adlayers of at least one of the particles decreases enough to allow particles in the domain to collapse under the van der Waals attraction, the threshold of this type of photomodification is determined by the temperature of the hottest particle. This temperature depends on the local environment of particles in the domain and on the local field enhanced by this environment. Accordingly, the temperature of small particles grows with the difference in particle size, which causes a monotonic decrease in the threshold of static photomodification for dimers and trimers with BS or BSB configurations.
The local field near the central particle in a monodisperse trimer is stronger than the local field near its lateral particles and stronger than the field near each particle in the dimer, which is in the presence of just one neighbor particle (given the same particle size and interparticle gaps). Therefore the maximum temperature is reached in the central particle of monodisperse trimer (except in the BSB configuration). Thus, the position of particles in a monodisperse trimer determines the photomodification and changes of optical and structural characteristics of the trimer.
In contrast, an additional and more significant factor for the manifestation of photomodification is the polydispersity of the plasmonic nanoparticles in aggregates. In highly polydisperse dimers or trimers, the hottest particle is always small, because big particles (or two big particles surrounding a small one) produce a higher local field at the small particle than the small particle does at a bigger one.
A single-particle resonance domain can be subjected only to dynamic reverse photomodification because of melting of the particle and its subsequent crystallization. Dynamic photomodification is also characteristic of multiparticle domains, and it is due to melting of one or more of the particles accompanied by a change in the absorption spectrum of the domain. Dynamic photomodification of colloidal aggregates under picosecond laser pulses always precedes their static photomodification.
The authors thank Prof. V. A. Markel (University of Pennsylvania) for supplying program codes with realization of the coupled dipole method for polydisperse nanoparticle aggregates. This work was performed within the state contract of the RF Ministry of Education and Science for the Siberian Federal University for scientific research in 2014 (Reference number 1792).
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|