In pursuit of further miniaturization and higher frequency operation of magnetic devices such as magnetic recording heads, planar inductors, and sensors, the study of soft magnetic thin films is a persistent interest. The granular films prepared from ferromagnetic metals (for example, Fe, Co, Ni, and their alloys) and insulated oxides (SiO₂, HfO₂, and Al₂O₃)^{[1– 3]} integrate high magnetic permeability μ , high electrical resistivity ρ (reducing the eddy loss), and moderate anisotropy field H_k (determining the frequency range under which the electromagnetic devices can be operated). For the application requirements, the study of damping phenomena of the dynamic magnetization is critical for obtaining the optimum high-frequency magnetic properties and understanding the dynamic magnetization process in soft-magnetic films. The phenomenological Landau– Lifshitz– Gilbert (LLG) model describes the dynamic magnetization behavior of magnetic moment^[4]

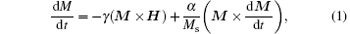
where γ is the gyromagnetic ratio, α is a phenomenological dimensionless damping factor, M_s is the saturation magnetization, and H is the effective field in the films. The first term on the right-hand side of the equation describes the procession of magnetic moment M around the external magnetic field H. The second term is phenomenological in nature and describes the magnetic energy dissipation.^[5] The damping factor α mentioned here is also a phenomenological value and is decided by the microstructure and the magnetic coupling properties. So any study of the damping factor, especially of how to tune α , is very significant for future applications.

Several studies were conducted of the contributions of different preparation technologies to the damping factor, including alternatives for fabricating the underlayer, ^[5] fabrication conditions, ^{[6– 8]} changing the film thickness, ^[9] and magnetic field annealing.^[10] However, studies related to the dependence of magnetization dynamics on the volume fraction of the ferromagnetic metal in a granular film system are still lacking. In our work, in a wide x range (the volume fraction of Ni₇₅Fe₂₅), ranging from 0.55 to 0.82, good soft-magnetic properties have been obtained in the (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular thin films. And high frequency properties are studied to analyze the dependence of damping properties on the variance of x. Study results indicate that the large and tunable damping coefficient α _eff can be obtained by adjusting the film microstructure.

(Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular thin films were deposited on water-cooled glass substrates by rf magnetron sputtering in a chamber with a base pressure of 6.0× 10^{− 4} Pa. The film thickness was kept constant at about 280 nm by controlling the sputtering time. A pure ZnO target (99.9%) and an Ni₇₅Fe₂₅ alloy target (99.9%) with the same diameter of 2 in (1 in = 2.54 cm) were used during the sputtering. The Ar gas pressure was maintained 0.12 Pa, and the Ar gas flux was fixed at 50 SCCM (SCCM donates cubic centimeters per minute at STP) during deposition. Both targets face the substrate with an incident angle of approximate 30° without an external magnetic field. The sputtering power for Ni₇₅Fe₂₅ was kept at 100 W, and the volume fractions of Ni₇₅Fe₂₅ were regulated by adjusting the power of ZnO. The powers of ZnO were 30 W, 40 W, 50 W, 60 W, and 70 W, respectively, and the corresponding measured volume fractions of ferromagnetic metal (x) were 0.82, 0.74, 0.64, 0.62, and 0.55, as determined by energy dispersive x-ray spectroscopy (EDS). Static magnetic properties (saturation magnetization M_s, coercivity H_c, and in-plane magnetic anisotropy field H_k) were measured by a vibrating sample magnetometer (VSM, Lake Shore model 7304). A surface profile meter (Dektak 6M) was employed to measure the thickness of films. The structure and microstructure were analyzed by x-ray diffraction (XRD) with Cu Kα radiation and high resolution transmission electronic microscopy (HRTEM), using a Tecnai-G2-F30 system, respectively. The microwave permeability measurements were carried out with a PNA E8363B vector network analyzer using the shorted microstrip transmission-line perturbation method, which works from 100 MHz to 5.5 GHz.

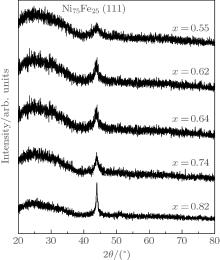
Figure 1 shows the XRD patterns of (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular thin films with different x values. Only one clear diffraction peak, indexed as face-centered cubic (fcc) Ni₇₅Fe₂₅ (111) was exhibited. As x decreases from 0.82 to 0.55, the Ni₇₅Fe₂₅ (111) diffraction peak becomes somewhat broader, reflecting the decrease of grain size. No diffraction peak corresponding to ZnO was found, indicating that the ZnO may be amorphous.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. XRD patterns of films with different volume fractions x.

TEM bright-field micrographs and their selected area electron diffraction (SAED) patterns of (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular films with x = 0.55, 0.64, and 0.82 are shown in Figs. 2(a), 2(b), and 2(c), respectively. The dark area is the Ni₇₅Fe₂₅ particles and the bright area corresponds to the ZnO matrix. It can be seen that as x decreases, the Ni₇₅Fe₂₅ particles are gradually wrapped by the semiconductor matrix. The average particle sizes obtained from HRTEM are about 13.2 nm, 5.7 nm, and 4.5 nm, corresponding to the samples with x = 0.55, 0.64, and 0.82. The grain size D can also be calculated through Scherrer’ s equation, as is shown in Fig. 2(d). With decreasing x, D decreases, which is consistent with the results from HRTEM. So it is obvious that the existence of the ZnO matrix impedes the growth of Ni₇₅Fe₂₅ particles. The microstructure of (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular thin films satisfies Herzer’ s model, ^[11] in that the average size D of magnetic particles is smaller than the ferromagnetic exchange length L_ex. An exchange interaction between particles may take place, which leads to good soft-magnetic properties.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. HRTEM micrographs for typical samples with x = 0.82 (a), x = 0.64 (b), x = 0.55 (c); the variation of mean particle size with x is shown in panel (d).

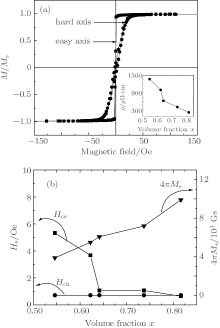
Figure 3(a) displays the hysteresis loops measured along the easy axis and hard axis at room temperature for a sample with x = 0.64. The hysteresis loop in the easy axis shows good squareness with smaller coercivity, and the film shows obvious in-plane uniaxial anisotropy. Figure 3(b) shows the dependence of coercivity (easy axis (H_ce) and hard axis (H_ch)) and saturation magnetization 4π M_s upon x. The saturation magnetization 4π M_s increases with increasing x. The H_ch remains nearly a constant, close to 1.0 Oe (1 Oe = 79.5775 A· cm^{− 1}), while H_ce varies from 5.3 Oe to 0.6 Oe with increasing x. In addition, the electrical resistivity ρ , shown in the inset of Fig. 3(a), increases up to 1370 μ Ω · cm with x decreasing from 0.82 to 0.55. Because the ferromagnetic metal particles are isolated, the scattering of conduction electrons increases, leading to higher electrical resistivity.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Hysteresis loops measured along the easy axis and hard axis for a typical sample of x = 0.64. (b) Volume fraction x dependence of 4π Ms, Hce, and Hch for (Ni75Fe25)x(ZnO)1− x granular films. The unit 1 Gs = 10− 4 T.

Figure 4 shows the frequency dependence of the complex permeability μ = μ ′ + iμ ″ for samples with different x values. By solving Eq. (1), one can obtain the complex permeability^[12]

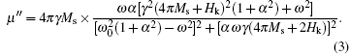
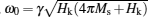
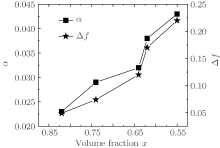
Here, and H_k is the in-plane uniaxial anisotropy field. All real and imaginary parts of the permeability can be well fitted with Eqs. (2) and (3). The values of M_s and H_k are measured by the VSM. The ferromagnetic resonance frequency (FMR) f_r has no obvious change for different x values. However, Δ f, the full width at half maximum of the resonance peak of the imaginary permeability spectra, increases as x decreases from x = 0.82 to x = 0.55, as is shown in Fig. 5 and is generally considered as the results of inhomogeneous and the Landau– Lifshitz magnetic damping.^{[13– 15]} The damping factor α _eff also shows the similar trend with Δ f.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Real part μ ′ and imaginary part μ ″ of the complex permeability of measured and fitted curves for samples with various volume fractions: (a) x = 0.82, (b) x = 0.74, (c) x = 0.64, (d) x = 0.62, (e) x = 0.55.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The volume fraction (x) dependence of damping factor α and frequency linewidth Δ f.

As reported previously, ^{[9, 15]}α _eff is generally divided into two parts: intrinsic part α _in and extrinsic part α _ext, and α _eff = α _int + α _ext. The α _int contributes to fundamental properties like the Zeeman transition, crystallographic or magnetic structure, while the two-magnon scattering and the local anisotropy dispersion contribute significantly to α _ext.^{[16, 17]} In our (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} nanogranular thin films, the microstructure is changed by tuning x, as is demonstrated by HRTEM patterns shown in Fig. 2. With decreasing x, the distance between ferromagnetic nanoparticles increases, resulting in the occurrence of the interparticle decoupling effect, ^[18] which contributes to the dispersion of spins and local anisotropy. Thus, α _ext, related with the microstructure, is the primary contribution to the effective damping factor α _eff, and α _eff can be tuned by adjusting the film microstructure. The α _eff of our granular films is bigger than that of most soft-magnetic films. For comparison, Table 1 summarizes the effective damping factor α _eff of several films that are good soft-magnetic films for high frequency applications. It can be seen that (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular films possess not only smaller coercivities but also larger damping factors α for a wide range of x.

Table 1.

Table 1.

Table 1. The effective damping factor α eff of several films. Composition α eff Hce/Oe Hch/Oe Reference FeCoN 0.007− 0.014 3.02− 10.9 3.54− 6.55 [6] FeCoSiN 0.007− 0.016 6.7− 10.5 4.3− 5.0 [19] CoAlO 0.03− 0.04 ∼ 22− 28 ∼ 7 [20] FeCoSi/native-oxide 0.026 8.4 − [21] (CoZr/SiO2)15 0.013− 0.017 2.5− 7.5 3.7− 8.3 [22] [Fe/SiO2]5 0.026− 0.07 8-30 7− 29 [23] FeNi− ZnO 0.023− 0.043 0.64− 5.33 0.02− 1.69 present

Table 1. The effective damping factor α eff of several films.

The large α _eff indicates that the (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} nanogranular thin films are ideal candidates for electromagnetic shielding applications in the high frequency range.

In conclusion of this paper, in a wide x range from 0.55 to 0.82, good soft magnetic properties have been obtained in (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} granular thin films. Permeability spectra of (Ni₇₅Fe₂₅)_x(ZnO)_{1− x} nanogranular thin films have been analyzed based on the phenomenological LLG equation. Study results indicate that the large and tunable damping coefficient α _eff can be obtained by adjusting the film microstructure (by changing x). The dependence of damping factor α upon x results mainly from the weakened exchange coupling between Ni₇₅Fe₂₅ particles.