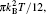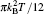Cite this Article
Zhu Guo-Bao, Yang Hui-Min, Yang Sheng-Yuan. Thermal and thermoelectric response from Keldysh formalism with application to gapped Dirac fermions* . Chinese Physics B, 2015, 24(4): 047401  
Permissions
Thermal and thermoelectric response from Keldysh formalism with application to gapped Dirac fermions*
Zhu Guo-Baoa),b)†, Yang Hui-Mina), Yang Sheng-Yuanc)
Department of Physics and Electronic Engineering, Heze University, Heze 274015, China
Institute of Theoretical Physics, Heze University, Heze 274015, China
Engineering Product Development, Singapore University of Technology and Design, Singapore 138682, Singapore

†Corresponding author. E-mail: zhuguobao@gmail.com

*Project supported by the Special Funds of the National Natural Science Foundation of China (Grant No. 11447145) and the Doctoral Program of Heze University, Shandong Province, China (Grant No. XY14B002).

Abstract

Based on the Keldysh Green’s functions theory, we present a general formula of the thermal and thermoelectric transport. In the clean limit, our formula recovers the previous results obtained from the semiclassical transport theory. In our approach, we propose an appropriate energy current operator and electric current operator, and the unphysical divergence from the direct application of the Kubo formula is eliminated. As an application, we study the thermal and the thermoelectric Hall conductivities of a gapped Dirac fermion model in the presence of impurity scattering.

Keyword: 74.25.fc; 73.50.Lw; 72.10.–d; 73.50.Bk; thermal; thermoelectric; Green’s function
1. Introduction

The study of energy transport in various systems has attracted a lot of attention.[1– 4] The control of the heat fluxes and minimization of the related energy loss are important factors in modern electronics. Energy transport in metals or semiconductors is mainly related to the electric current flow. Electrons move in the materials, carrying not only charge but also energy. A temperature gradient can generate both electric current and energy (heat) current. In linear response, the electric and thermal transport induced by a temperature gradient is given by the following relation

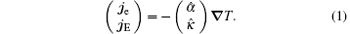
where je and jE represent the electric and heat current densities, respectively. 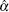is the thermoelectric conductivity tensor and the coefficient is the thermal conductivity tensor.

Transport properties can be affected by electrical, optical, and magnetic means. The corresponding mechanical force on the carriers are the electric force and the Lorentz force; however, there is no mechanical force that corresponds to the temperature gradient. Therefore, many of the theoretical tools which are used to describe charge (spin) transport cannot be straightforwardly extended to the study of heat transport. The direct application of linear response theory typically yields unphysical divergence[5– 7] at zero temperature. In this paper, by choosing an appropriate energy operator and electric current operator with auxiliary gravitational field we are able to derive general formulas for the thermal and thermoelectric conductivities based on the Keldysh Green functions theory.[8– 16] The method can eliminate the troublesome divergence from the direct application of the Kubo formula. We show that in the clean limit, our formula reduces to the previous results obtained from other approaches. Expressed in terms of Green’ s function, our result has the advantage that disorder effects and interaction effects can be systematically studied using the standard perturbation method. As an application, we study the thermal and thermoelectric Hall conductivities in a disordered gapped Dirac model.

The structure of this paper is organized as follows. In Section  2 we derive our general formula of thermal and thermoelectric conductivities. In Section  3, we present the application of our formula to study the thermal and thermoelectric Hall conductivities in the disordered gapped Dirac fermion model. In Section  4, we summarize our results.

2. Formula

In this section, we derive the thermal and thermoelectric transport coefficients in the presence of the temperature gradient in the linear response regime. However, it is not possible to directly incorporate the temperature gradient into the Hamiltonian as an external field. This is because the temperature gradient is a statistical force that affects the particles through the distribution function rather than a dynamical force that exerts direct force to the particle. To solve this problem, Luttinger[17] proposed a method to study first the response due to the mechanic force from an inhomogenous gravitational field, then using the Einstein relation to relate the obtained transport coefficients to the thermal transport coefficients.

We follow Luttinger’ s method, and introduce an auxiliary gravitational field γ to the Hamiltonian. In the presence of gravitational field γ corresponding to the mechanic counterpart of the temperature gradient, the term in Hamiltonian due to the interaction with this field[9] is

We note that by including the interaction, the velocity operator becomes

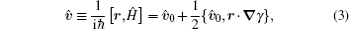
and the energy current operator becomes

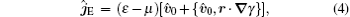
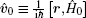
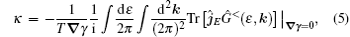
where , [A, B] = AB − BA, {A, B} = AB + BA and Ĥ = Ĥ 0 + Ĥ int. Hence the velocity and energy current operators have additional contributions from the inhomogeneity of the gravitational field. In Keldysh formalism, the total transport current which is proportional to Tr[jĜ < ] therefore has an additional contribution proportional to ∇ γ . According to Luttinger’ s argument based on the Einstein relation, the ratio between this contribution and T∇ γ just leads to the thermal transport coefficients. Explicitly, the corresponding thermal and thermoelectric conductivity tensors can be written as

where lesser Green’ s function Ĝ < (ε , k) can be determined by introducing the auxiliary gravitational field γ into the Dyson equation. The Dyson equation for Green’ s function in the presence of Luttinger’ s gravitational field γ (r) is

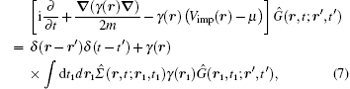
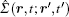
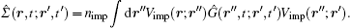
where Ĝ (r, t; r′ , t′ ) = − i 〈 Tc{ψ (r, t)ψ † (r′ , t′ )}〉 is the contour-ordered Green’ s function matrix, and is the corresponding self-energy matrix. Tc{· · · } is the time-ordering operator, and ψ (r, t) and ψ † (r, t) are the annihilation and creation operators for quasiparticles. In the Born approximation we have

Where nimp and Vimp denote a possible disorder concentration and potential respectively. By applying the following transformation to the Dyson equation  (7)

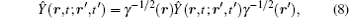
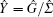
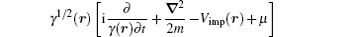
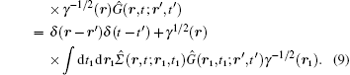
with , we obtain

After Fourier transforming the relative time, the Dyson equation in the linear response regime becomes

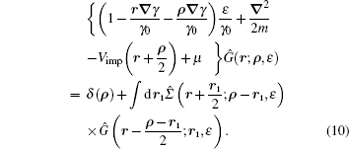
Here we separated the dependence on the center of mass and the relative coordinates. Then, we have the ∇ γ -dependent part of the Green function given by

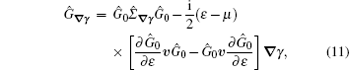
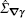
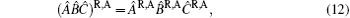
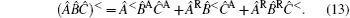
where Ĝ ∇ γ and are the ∇ γ -dependent part of the Green function and the self-energy respectively. In Keldysh space, the product of matrices obeys the following rules[18]

Using the above relations, we can separate G< into two terms: a Fermi surface contribution and a Fermi sea contribution

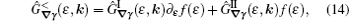
where

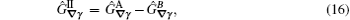
and

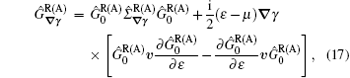
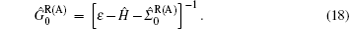
First we consider the simplest clean limit result. This also serves as a check of our theory. In this case, the retarded and advanced Green’ s functions are just given by

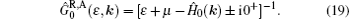
Ĥ 0 is disorder free part of the Hamiltonian. Plugging Eq.  (19) into Eq.  (6), we can obtain

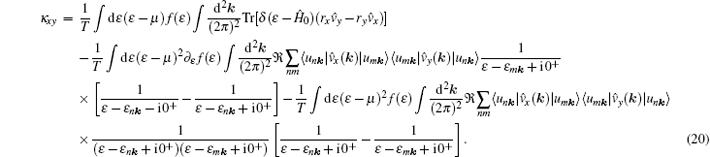
Using the residue theorem, we find that

After some algebra (the same procedure described in Refs.  [9] and [10]), we obtain

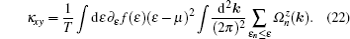
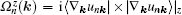
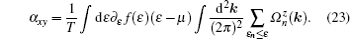
Here is the Berry curvature of the Bloch state | n, k〉 = eik· r/ħ | unk〉 . This clean limit result was previously derived by Qin et al.[6] and Matsumoto et al.[7, 8] Now it is also reproduced as a special limiting case of our general formula. For the thermoelectric conductivity in the clean limit, we have

3. Model and results
3.1. Dirac model

In the following we apply our derived formula to study the thermal and thermoelectric Hall conductivities of the 2D gapped Dirac model. This model has been widely used to describe systems such as gapped graphene and gapped topological insulator surfaces.[19, 20] It can be written as

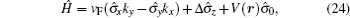
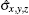
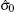
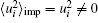
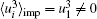
where are the Pauli matrices and is the identity matrix. vF is a constant representing the velocity. The second term represents a gap opened in the spectrum due to certain symmetry breaking effects. For topological insulator surfaces, this could originate from the Zeeman field or exchange field produced by magnetic doping or nearby magnetic layers. Here, we consider the spin-independent random impurities V(r) = ∑ riuiδ (r − ri), with the impurities potential ui, and the impurities concentration ni. ri is the random locations of the scattering centers, and we assume the disorder has the following statistical properties 〈 ui〉 imp = 0, , and . The band dispersions of the clean system are

the corresponding wave functions are

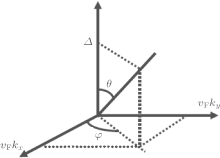
Where φ = arctan(ky/kx) is the azimuthal angle (see Fig.  1),

is the polar angle (see Fig.  1), and we have unitized the size of the system.

Fig.  1. Schematic diagram for azimuthal angle φ and polar angle θ .

3.2. Results

In the following we consider that the system is electron doped with ε F > Δ . Due to particle hole symmetry, the results can be easily generalized to the hole-doped case. In our model, we assume that the impurities are dilute, and then we obtain the self-energy using Born approximation[21]

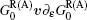
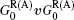
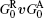
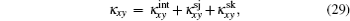
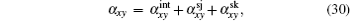
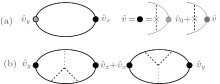
Since we have assumed that is the relaxation time, [21] and the real part of the self-energy can be neglected. The effect of in Eq.  (17) is canceled out. This is similar to the case of the perturbation from an electric field.[12] The terms and are of higher order in 1/ε Fτ , hence only the disorder free part of these term is important to physical quantities.[21, 22] Therefore, the disorder effects are contained in the term . The thermal and thermoelectric Hall conductivity can be decomposed in the following way (see Fig.  42(a) in Ref.  [22])

where the first term denotes an intrinsic Berry curvature-driven contribution, and the other two terms caused by the scattering of electrons off impurities: the side-jump contribution and the skew-scattering contribution.[23] According to the diagrammatic representation as shown in Fig.  2, the side-jump contribution and skew-scattering contribution to thermal and thermoelectric conductivity are

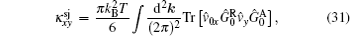
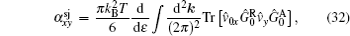
and

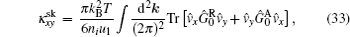
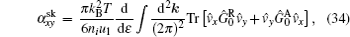
respectively. Where

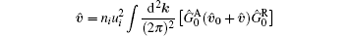
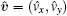
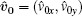
is the ladder-diagram corrected velocity vertex, , and .

Fig.  2. Graphical representation (a) of the side-jump contribution and (b) of the skew-scattering contribution. The solid lines are the disorder averaged Green’ s functions, and the dashed lines with crosses represent disorder scattering.

When ε F > Δ , the intrinsic contributions (above band gap) can be calculated by Eqs.  (22) and (23) using Sommerfeld expansion, and we have

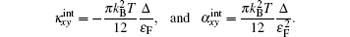
Straightforward calculations show that

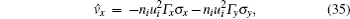
Where

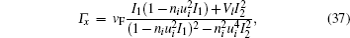
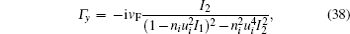
and

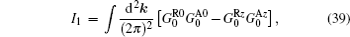
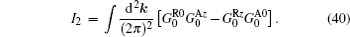
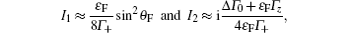
are the i-th components of advanced (α = A) and retarded (α = R) Green’ s functions in the Pauli matrix representation, i.e., . In the weak scattering limit,

when both subbands are partially occupied, i.e., ε F > Δ , where sinθ F = γ kF/ε F. Then we obtain

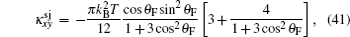
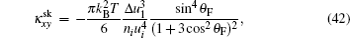
and

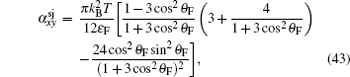
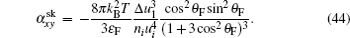
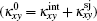
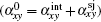
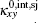
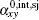
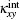
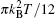
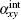
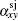
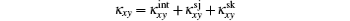
The skew scattering contribution only dominates in the ultraclean limit.[22] Here we are most interested in the sum of intrinsic and side-jump thermal and thermoelectric Hall conductivity . We only include the intrinsic contribution from the conduction band.[24] The extra contributions from the fully occupied valence bands are beyond the description of the effective model here. In comparison, the extrinsic contribution comes from electrons near the Fermi surface, so they are well-captured in the effective model. In Fig.  3. we plot and as a function of the Fermi energy ε F. and approach a constant value asymptotically as ε F ⟶ ∞ , while , , and approach 0 value asymptotically as ε F → ∞ . They change sign at ε F ≈ 7.3Δ and ε F ≈ 2.1Δ , respectively. Because the extrinsic contribution to the thermal Hall conductivity has opposite sign as compared with the intrinsic contribution and they compete as the Fermi energy varies. These behaviors are similar to the anomalous Hall conductivity.[22, 24] Indeed, for good metals, the thermal Hall conductivity

can be obtained from anomalous Hall conductivity[22, 23] based on Wiedemann– Franz law. The thermoelectric Hall conductivity

can be obtained from anomalous Hall conductivity based on the Mott rule. The calculations here again demonstrate the validity of our formula.

Fig.  3. The intrinsic contribution (dashed blue curve), side-jump contribution (dash-dotted green curve), and their sum (solid red curve) to thermal Hall conductivity (a), and thermoelectric Hall conductivity (b) as a function of the Fermi energy ε F. The thermal Hall conductivity is measured in units of and the thermoelectric Hall conductivity is measured in units of .
4. Conclusion

In summary, we have derived a general formula of the thermal and thermoelectric transport of disordered electron systems based on the Keldysh Green’ s functions theory. Following the method proposed by Luttinger, we proposed an appropriate energy current operator and electric current operator. The unphysical divergence from the direct application of the Kubo formula is eliminated in our approach. In the absence of disorders, our formula recovers the previous results obtained from the semiclassical theory. As an application, we studied extrinsic thermal and thermoelectric Hall conductivities of a disordered gapped Dirac model. Our theory would be useful for systematic studies of disorder and interaction effects in thermal transport phenomena.

Reference
1 Dubi Y and Ventra M D 2011 Rev. Mod. Phys. 83 131 DOI:10.1103/RevModPhys.83.131 [Cited within:1] [JCR: 44.982]
2 Xiao X X, Xie W J, Tang X F and Zhang Q J 2011 Chin. Phys. B 20 087201 DOI:10.1088/1674-1056/20/8/087201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
3 Wu J Bo, Tang X G, Jia Z H, Chen D G, Jiang Y P and Liu Q X 2012 Acta Phys. Sin. 61 207702(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
4 Meng D Y, Shen L X, Shai X X, Dong G J and Deng S K 2013 Acta Phys. Sin. 62 247401(in Chinese) DOI:10.7498/aps.62.247401 [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
5 Qin T, Niu Q and Shi J 2011 Phys. Rev. Lett. 107 236601 DOI:10.1103/PhysRevLett.107.236601 [Cited within:1] [JCR: 7.943]
6 Matsumoto R and Murakami S 2011 Phys. Rev. Lett. 106 197202 DOI:10.1103/PhysRevLett.106.197202 [Cited within:1] [JCR: 7.943]
7 Matsumoto R and Murakami S 2011 Phys. Rev. B 84 184406 DOI:10.1103/PhysRevB.84.184406 [Cited within:2]
8 Smrčka L and Strěda P 1977 J. Phys. C: Solid State Phys. 10 2153 DOI:10.1088/0022-3719/10/12/021 [Cited within:2]
9 Vafek O, Melikyan A and Tečnović Z 2001 Phys. Rev. B 64 224508 DOI:10.1103/PhysRevB.64.224508 [Cited within:2]
10 Onoda S, Sugimoto N and Nagaosa N 2006 Phys. Rev. Lett. 97 126602 DOI:10.1103/PhysRevLett.97.126602 [Cited within:1] [JCR: 7.943]
11 Onoda S, Sugimoto N and Nagaosa N 2008 Phys. Rev. B 77 165103 DOI:10.1103/PhysRevB.77.165103 [Cited within:1]
12 Michaeli K and Finkel’stein A M 2009 Phys. Rev. B 80 115111 DOI:10.1103/PhysRevB.80.115111 [Cited within:1]
13 Michaeli K and Finkel’stein A M 2009 Phys. Rev. B 80 214516 DOI:10.1103/PhysRevB.80.214516 [Cited within:1]
14 Kovalev A A, Tserkovnyak Y, Vyborny K and Sinova J 2009 Phys. Rev. B 79 195129 DOI:10.1103/PhysRevB.79.195129 [Cited within:1]
15 Kovalev A A, Sinova J and Tserkovnyak Y 2010 Phys. Rev. Lett. 105 036601 DOI:10.1103/PhysRevLett.105.036601 [Cited within:1]
16 Zhu G B, Yang S A, Fang C, Liu W M and Yao Y G 2012 Phys. Rev. B 86 214415 DOI:10.1103/PhysRevB.86.214415 [Cited within:1]
17 Luttinger J M 1964 Phys. Rev. 135 A1505 DOI:10.1103/PhysRev.135.A1505 [Cited within:1] [JCR: 6.583]
18 Rammer J and Smith H 1986 Rev. Mod. Phys. 58 323 DOI:10.1103/RevModPhys.58.323 [Cited within:1] [JCR: 44.982]
19 Lu H Z, Shi J R and Shen S Q 2011 Phys. Rev. Lett. 107 076801 DOI:10.1103/PhysRevLett.107.076801 [Cited within:1] [JCR: 7.943]
20 Krstajić P M and Vasilopoulos P 2012 Phys. Rev. B 86 115432 DOI:10.1103/PhysRevB.86.115432 [Cited within:1]
21 Misawa T, Yokoyama T and Murakami S 2011 Phys. Rev. B 84 165407 DOI:10.1103/PhysRevB.84.165407 [Cited within:3]
22 Nagaosa N, Sinova J, Onoda S, MacDonald A H and Ong N P 2010 Rev. Mod. Phys. 82 1539 DOI:10.1103/RevModPhys.82.1539 [Cited within:5] [JCR: 44.982]
23 Sinitsyn N A, MacDonald A H, Jungwirth T, Dugaev V K and Sinova J 2007 Phys. Rev. B 75 045315 DOI:10.1103/PhysRevB.75.045315 [Cited within:2]
24 Yang S A, Pan H, Yao Y and Niu Q 2011 Phys. Rev. B 83 125122 DOI:10.1103/PhysRevB.83.125122 [Cited within:2]