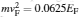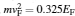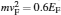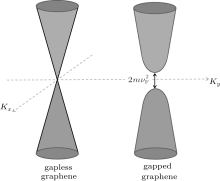
As is well known, graphene is a two-dimensional monolayer of graphite.^[1] Its unique properties are indicated to be an appropriate candidate for constructing electronic and spintronic devices.^{[2, 3]} The carriers in the graphene fabricated on SiO₂ are massless relativistic particles with a linear dispersion relation near the K point (E (k) = ℏ kv_F) where v_F (∼ 10⁶ m/s) is the Fermi velocity (Fig. 1(a)).

Recent studies show that despite the extremely high carrier mobility of gapless graphene, it is necessary to open a gap between the conduction and valence bands of graphene in order to realize some device functions, ^{[4– 6]} so opening and tailoring a band gap in graphene is probably one of the most important and urgent research topics in graphene research currently.^{[7– 9]}

Since the electronic properties are strongly related to the delocalized electrons in graphene, obviously any modification will influence the electronic properties of the system. To gain the two-dimensional gapped graphene, the possible experimental approaches include the epitaxial growth of a graphene monolayer on an SiC or BN substrate. It is estimated that the graphene sample opens a band gap of about 50 meV on a boron– nitride substrate, ^{[6, 10]} and it opens about 260 meV on a silicon– carbide substrate.^[11] The carriers in gapped graphene are fermions like massive Dirac particles (see Fig. 1(b)). Unique features of graphene motivate researchers to study electronic and spintronic transport properties of graphene-based systems^{[12– 38]} as well as photonics and plasmonics.^{[39– 42]}

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Energy spectra of quasiparticles in (a) gapless and (b) gapped graphene.

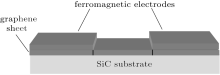
In this paper, we consider clean gapped graphene-based ferromagnetic/normal/ferromagnetic (FG/NG/FG) junctions where the graphene is fabricated on the SiC and BN substrates separately. The ferromagnetic state can be induced by depositing a ferromagnetic insulator on top of graphene.^[43] The magnitudes of the graphene energy gap 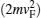for SiC and BN substrates are 260 meV and 50 meV, respectively and the Fermi energy in the normal graphene region (E_FN) is 400 meV.

Our model is composed of two similar ferromagnetic layers separated by a normal graphene of thickness L (Fig. 2). Direction of the magnetization of the left ferromagnet is fixed to be upward but the right ferromagnet has magnetization parallel (up) or antiparallel (down) to the magnetization direction of the left ferromagnet. The system is considered to be in the xy-plane. Since the considered graphene nanoribbon is short and wide (i.e., W/L ≫ 1, where L is the thickness of the normal graphene region and W is the width of the graphene sheet), microscopic details of edge and chirality are both neglected.^{[44, 45]}

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Schematic illustration of a gapped FG/NG/FG junction.

The wave functions describing the quasiparticles are the solutions of the massive Dirac– Bogoliubov– de Gennes equation defined as

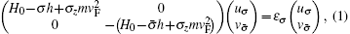
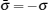
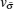
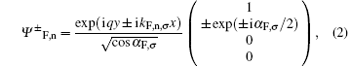
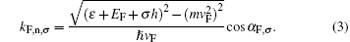
where H₀ = − iℏ v_F(σ _x∂ _x ± σ _y∂ _y) − E_FN, with σ _x, σ _y, and σ _z being 2 × 2 Pauli matrices; ε _σ is the energy of quasiparticles related to the Fermi level; E_FN is the Fermi energy of normal graphene; h is the magnetization exchange energy; v_F denotes the Fermi velocity of quasiparticles; σ = ± 1 for up and down spins of quasiparticles; . Both u_σ and (electron and hole-like quasiparticle wave functions) have two components of sublattices in the hexagonal lattice of graphene. The solution to Eq. (1) can be clearly seen in different regions. In the ferromagnetic region, wave functions are given by

While for the normal graphene region

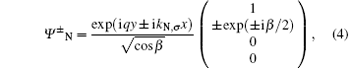
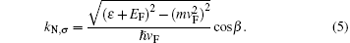
Here k_{F, n, σ} and k_{N, σ} are the components of electron-like wave vector perpendicular to the interface in ferromagnetic and normal graphene regions, respectively. In our calculations, we have in the two-dimensional plane of graphene. Also, α _{1, σ} are injection angles of electron-like quasiparticles in the first ferromagnetic region, with respect to the axis normal to the interface. α _{F, σ} and β as the incident angles in the second ferromagnetic and normal graphene regions, are calculated using the conservation of momentum in the y direction.

The refection coefficient r and the transmission coefficient t are calculated by applying the boundary conditions at the interface between ferromagnetic and normal regions. The interfaces between ferromagnets and normal graphene are perpendicular to the x axis at x = 0 and x = L, that is

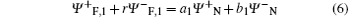
for x = 0, and

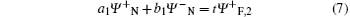
for x = L. Using the boundary conditions (6) and (7), the transmission coefficient for the antiparallel case is obtained as follows:

For the parallel case we only need to set α _{F, σ} = α _{1, σ} .

Using the approach of Refs. [46]– [48], the differential electronic conductance at zero temperature is

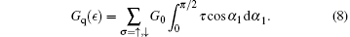
For differential spin conductance at zero temperature, we have

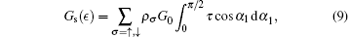
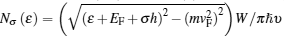
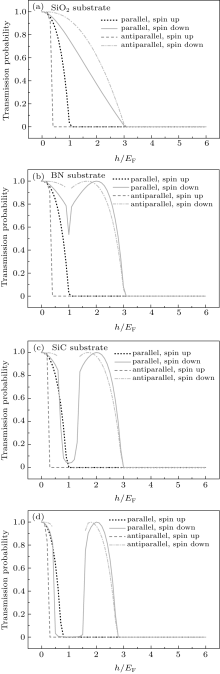
where G₀ = 2e²/hN_σ (ϵ V) is spin-dependent normal conductance, ρ _σ = + 1 (− 1) for σ = ↑ (↓ ), and the density of states is with W being the width of the graphene-based FNF junction.

Figure 3 demonstrates the transmission probability (τ = | t| ²) of quasiparticles in terms of the exchange energy of ferromagnets in parallel and antiparallel structures for a gapless case and three gapped cases.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Transmission probabilities of electrons versus h/EF of ferromagnets, here, the thickness of the graphene-based normal region is kL= 10. (a) Gapless graphene, (b) gapped graphene fabricated on BN substrate, , (c) gapped graphene fabricated on SiC substrate, , (d) gapped graphene with arbitrary gap size, .

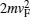
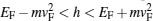
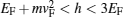
It is observed that for h/E_F > 3 the transmission probability is zero for all cases. Also there is an energy interval around the Fermi energy with a size of graphene gap of in which the transmission probabilities of spin-down quasiparticles are negligible in both parallel and antiparallel structures. However, the considered gapless structure can be used for only spin-down polarized current. It is clear that in gapped cases both spin-up and spin-down polarized currents may be produced. Since the transmission probability for the exchange energies is nonzero only for spin-up quasiparticles in parallel setup and in the cases of a large graphene gap, we can use the parallel setup to obtain spin-up polarized current. Like the gapless case, for the exchange energies the spin-down polarized current passes through the antiparallel structure of gapped setups.

Figures 4 and 5 show the charge conductances of parallel and antiparallel structures versus h/E_F of ferromagnets, respectively.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Normalized charge conductances of parallel structure versus h/EF of ferromagnets. Here, the thickness of the graphene-based normal region is kL= 10.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Normalized charge conductances of antiparallel structure versus h/EF of ferromagnets. Here, the thickness of graphene-based normal region is kL= 10.

Increasing the strength of ferromagnet h, the potential well will be deeper and charge transport suppresses. It can be seen that the conductance diagrams of gapped parallel structures in terms of the exchange-energy have a special behavior at the energies close to 2E_F. For the antiparallel structures, the special behavior at energy close to E_F can be seen for both gapless and gapped structures. 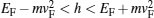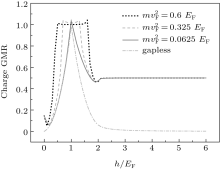Also in the range of , which is the magnitude of the graphene energy gap, the charge conductances of all gapped structures are zero. Since a giant magnetoresistance (GMR) effect is observed as a significant change in the electrical resistance depending on whether the magnetizations of ferromagnetic layers are in a parallel or an antiparallel alignment, the latter case leads to perfect charge gaint magnetoresistance (GMR) in this energy range for gapped graphene-based FG/NG/FG junctions as shown in Fig. 6.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Charge GMRs versus h/EF of ferromagnets. Here, the thickness of graphene-based normal region is kL= 10 .

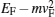
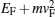
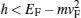
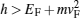
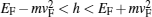
Figures 7 and 8 show spin conductances of parallel and antiparallel structures versus h/E_F of ferromagnets. The spin conductance of the gapped parallel structure has different behaviors in energies less than from those in energies greater than . The difference is due to the distinct behavior in the number of available states which decreases with increasing the exchange energy for exchange energies , but for exchange energies with increasing the exchange energy, the number of available states increases. Also it is clear that the spin conductances of gapped parallel structures have considerable values in exchange energies and the size of this interval is equal to graphene energy gap.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Normalized spin conductances of parallel structure versus h/EF of ferromagnets. Here, the thickness of the graphene-based normal region is kL= 10.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Normalized spin conductances of antiparallel structure versus h/EF of ferromagnets. Here, the thickness of the graphene-based normal region is kL= 10.

Unlike the parallel structure case, the only effect of increasing the graphene energy gap is to reduce the spin conductance of the antiparallel structure, which has significant magnitude in energy around h ∼ 2E_F.

Since parallel and antiparallel spin conductances have significant values in different ranges of energies (except E_F < h < 2E_F), the spin GMR is almost 1 in most exchange energies as illustrated in Fig. 9.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Spin GMRs versus h/EF of ferromagnets.

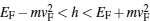
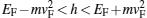
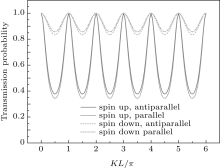Our calculations show oscillating dependences of transmission probability, charge, and spin conductance on the thickness of the normal graphene region for all exchange energies except (Figs. 10 and 11). This is because of the interference between incident and reflected quasiparticles from the two different FN interfaces inside the normal region.^{[49– 52]} In the range of , there is a damping factor for all quasiparticles except spin-up quasiparticles in the parallel setup.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Transmission probabilities of electrons versus thickness of the normal region, h = 4EF.

Fig. 11.

	Figure Option ViewDownloadNew Window
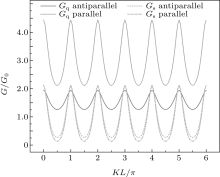	Fig. 11. Charge and spin conductance of electrons versus thickness of the normal region, h = 4EF.

We studied the electronic and spintronic conductances in parallel and antiparallel clean gapped graphene-based FG/NG/FG junctions by taking into account the effect of the exchange energy of magnetic layers and thickness of the normal graphene region.

In our calculations, the experimental data given in Refs. [6], [10], and [11] are used. For gapped graphene grown on SiC and BN substrates, the values of energy gap are 260 meV and 50 meV, respectively and the Fermi energy of the normal graphene region (E_FN) is 400 meV.

It is illustrated that despite gapless FG/NG/FG structures, which can be used to acquire spin-up (or spin-down) polarized current (see Ref. [16]), the gapped FG/NG/FG structures can be used for both spin-up and spin-down polarized currents. It means that they can be used as a spin-polarized current switch. Also in the gapped FG/NG/FG structure, perfect charge GMR is observed in the range of while in the case of gapless FG/NG/FG structure, perfect charge GMR is obtained only in h = E_F. The transmission property in gapped structure has an oscillating dependence on the thickness of the normal graphene layer, which is similar to that in the gapless FG/NG/FG structure.