Cite this Article
Li Yi, Liu Jian, Wang Chun-Lei, Su Wen-Bin, Zhu Yuan-Hu, Li Ji-Chao, Mei Liang-Mo. Thermoelectric properties of Sr0.61Ba0.39Nb2O6− δ ceramics in different oxygen-reduction conditions* . Chinese Physics B, 2015, 24(4): 047201  
Permissions
Thermoelectric properties of Sr0.61Ba0.39Nb2O6− δ ceramics in different oxygen-reduction conditions*
Li Yia), Liu Jiana),b)†, Wang Chun-Leia),b), Su Wen-Bina),b), Zhu Yuan-Hua), Li Ji-Chaoa),b), Mei Liang-Moa),b)
School of Physics, Shandong University, Jinan 250100, China
State Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China

†Corresponding author. E-mail: liujjx@sdu.edu.cn

*Project supported by the National Basic Research Program of China (Grant No. 2013CB632506) and the National Natural Science Foundation of China (Grant Nos. 51202132 and 51002087).

Abstract

The thermoelectric properties of Sr0.61Ba0.39Nb2O6− δ ceramics, reduced in different conditions, are investigated in the temperature range from 323 K to 1073 K. The electrical transport behaviors of the samples are dominated by the thermal-activated polaron hopping in the low temperature range, the Fermi glass behavior in the middle temperature range, and the Anderson localized behavior in the high temperature range. The thermal conductivity presents a plateau at high-temperatures, indicating a glass-like thermal conduction behavior. Both the thermoelectric power factor and the thermal conductivity increase with the increase of the degree of oxygen-reduction. Taking these two factors into account, the oxygen-reduction can still contribute to promoting the thermoelectric figure of merit. The highest ZT value is obtained to be ∼0.19 at 1073 K in the heaviest oxygen reduced sample.

Keyword: 72.15.Jf; 72.20.Ee; Sr0.61Ba0.39Nb2O6− δ, electrical transport mechanism, thermoelectric figure of merit, thermal conductivity
1. Introduction

Thermoelectric materials can be used to convert thermal energy and electrical energy into one another, which is of significance for environmentally friendly refrigeration and waste heat recycling. The thermoelectric conversion efficiency is evaluated by the thermoelectric figure of merit ZT = S2T/ρ κ , where S is the Seebeck coefficient, T is the absolute temperature, ρ is the electrical resistivity, and κ is the thermal conductivity. Although heavy-metal-based thermoelectric materials, such as (Bi, Sb)2(Te, Se)3, SiGe, PbTe, and relevant semiconductors, have been well studied, [1– 7] there are some limitations, for instance, high costs, instability at high temperatures, and dependence on rare or toxic elements.[8– 10] Oxide thermoelectric materials can solve these problems, [8, 9] but the thermoelectric properties of oxide are still far from practical application. Therefore, it is significant to find new oxide thermoelectric materials with high ZT values.

In recent research, tungsten bronze-structured ferroelectric Sr1− xBaxNb2O6− δ (SBN) was found to be a promising n-type thermoelectric oxide. Scientists observed that Sr0.61Ba0.39Nb2O6− δ (SBN61) single crystals have a high thermoelectric power factor (∼ 2000  μ W/mK2 at 516  K) in the direction parallel to the c axis.[10] In the SBN structure, the Nb– O octahedron is interconnected orderly along the c axis, and shows a complex arrangement in the ab plane. There are many voids among the Nb– O octahedron, occupied by Sr2+ or Ba2+ ions. The complex system has previously been concerned with its low thermal conductivity, [10– 12] which may contribute to the enhancement of the thermoelectric figure of merit. In the oxygen reduced SBN61 ceramics, the oxygen vacancy concentration, the electron concentration, and the ratio of Nb4+ /Nb5+ all increase through the oxygen-reduction treatment. The negative charge carriers contribute to the electrical conductivity, and the oxygen vacancies and Nb4+ ions may influence the thermal conduction.[10] As a new thermoelectric oxide, there are many questions that remain to be investigated. For example, the thermal conductivity and exact ZT values of SBN61 ceramics have not been reported yet. In this paper, we measure the thermoelectric properties of the oxygen reduced Sr0.61Ba0.39Nb2O6− δ ceramics. The electrical conduction mechanism and the thermal conduction behavior are analyzed in detail. The influence of oxygen-reduction on thermal properties is discussed, and it is concluded that the heavily oxygen-reduction effectively enhance the thermoelectric figure of merit of SBN61 ceramics.

2. Experiment

Sr0.61Ba0.39Nb2O6− δ ceramic samples were prepared with using SrCO3 (99.8%), BaCO3 (99.8%), and Nb2O5 (99%) powders by the solid-state reaction technique. Appropriate quantities of the starting materials were ground and pressed into pellet discs. These discs were calcined at 1200  ° C for 6  h in an air atmosphere. After intermediate grinding and pressing, the discs were sintered at 1400  ° C in an air atmosphere. Then the discs were annealed at 1100  ° C or 1250  ° C for 10  h in pure argon or forming gas (5-mol% hydrogen in argon) with a flow rate of 0.2  l/min. The phase structures were characterized by powder x-ray diffraction (XRD) with a Rigaku D/MAX-2550P diffractometer using Cu Kα radiation (λ = 0.154056 nm). A scanning electron microscope (SEM, Hitachi SU-70) equipped with an energy dispersive spectrometer (EDS) was used for evaluating the microstructure and composition. The thermal conductivity was calculated from the same thermal diffusivity, specific heat capacity, and sample density as that measured by a laser flash apparatus (Netzsch LFA 427), a thermal analyser (Netzsch STA 449C), and the Archimedes’ method, respectively. The sintered discs were cut into rectangular columns (16  mm× 2  mm× 2  mm) for measurements of the Seebeck coefficient and the electrical conductivity using a Linseis LSR-3/1100 instrument in helium atmosphere by a modified dynamic method.[13]

3. Result and discussion
3.1. The x-ray diffraction and SEM analysis

In Fig.  1 we shows the x-ray diffraction patterns of the SBN61 samples in various oxygen-reduction conditions. The XRD patterns show that the profile of each sample includes all the diffraction peaks of tungsten bronze-structured Sr0.61Ba0.39Nb2O6. It is found that the NbO2 second phase is in the heavily oxygen-reduced sample SBN61H1250. The Nb4+ /Nb5+ ratio is increased by the oxygen-reduction reaction, and the Nb4+ O2 second phase will appear with the increase of Nb4+ /Nb5+ content.[11] Referring to Lee et al.’ s[10] paper, both the reductive forming gas and the high annealing temperature contribute to deepening the oxygen-reduction degree, so the oxygen-reduction degree increases in the order of SBN61Ar (annealed at 1250  ° C in argon), SBN61H1100 (annealed at 1100  ° C in a gas mixture of H2/Ar), and SBN61H1250 (annealed at 1250  ° C in a gas mixture of H2/Ar).

The densities and lattice parameters of the samples are shown in Table  1. The lattice parameters do not vary monotonically with increasing the degree of oxygen-reduction. The non-monotonic variations of the lattice parameters may be affected by many factors, such as the oxygen vacancies, the larger radii of Nb4+ than Nb5+ , and the bond angles in the NbO6 octahedrons.[11] The relative densities are calculated, which are also shown in Table  1. All the samples have high relative densities above 96.5%. Figure  2 shows the SEM micrographs of samples SBN61Ar and SBN61H1250. The average grain size is 3.11  μ m and 2.83  μ m for SBN61Ar and SBN61H1250, respectively. As seen from Fig.  2, the SBN61 ceramics have compact grains for both heavily and slightly oxygen reduction degrees. As shown in Fig.  2(b), there are two kinds of grains: coarse grains and slender grains. According to the results of EDS, the coarse grains are of the SBN61 crystal and the slender grains are of the NbO2 second phase. These slender grains do not exist in the sample SBN61Ar as shown in Fig.  2(a), which is consistent with the XRD result.

Fig.  1. XRD patterns for SBN61 ceramics. The samples are annealed at 1250  ° C in argon (SBN61Ar), 1100  ° C in a gas mixture of H2/Ar (SBN61H1100), and 1250  ° C in a gas mixture of H2/Ar (SBN61H1250), respectively. The NbO2 second phase is marked by solid squares in the figure.

Table 1. Lattice parameters (a, b, c), theoretical densities (ρ th), measured densities (ρ m), and relative densities (ρ r) of the samples.

Fig.  2. The SEM micrographs (2000× ) of samples SBN61Ar (a) and SBN61H1250 (b).

3.2. Seebeck coefficient and electrical resistivity

Figure  3 shows the results of electrical resistivity ρ and the Seebeck coefficient S for samples SBN61Ar, SBN61H1100, and SBN61H1250. The electrical resistivity and the Seebeck coefficient are measured intensively below 623  K. As shown in Fig.  3, the temperature dependences of Seebeck coefficient and electrical resistivity below 508  K are similar to those in the slightly reduced SBN61 ceramics reported by Lee et al.[11] However, in Lee et al.’ s report, the temperature dependence of the Seebeck coefficient changes in the lower pO2 annealed sample. This distinction may be ascribed to the higher annealing oxygen partial pressure in our experiment. Moreover, we measure the Seebeck coefficient and the electrical resistivity up to 1073  K and find a different conduction behavior in the high temperature region (above 508  K). As shown in Figs.  3(a) and 3(b), both the electrical resistivity and the magnitudes of the Seebeck coefficient decrease with the deepening oxygen-reduction degree, which accords with Lee et al.’ s results.[11] As a result, the thermoelectric power factor (PF = S2/ρ ) is enhanced from 182  μ W/K2m (in SBN61Ar at 1073  K) to 375  μ W/K2m (in SBN61H1250 at 1073  K).

Fig.  3. Plots of S versus T (a) and ρ versus T (b) for samples SBN61Ar, SBN61H1100, and SBN61H1250. The inset in Fig.  3(b) shows the plots of ρ versus T in a temperature range from 500  K to 1100  K.

In the following, the electrical transport properties are discussed in detail. The Seebeck coefficient directly reflects the behavior of the band structure and is less influenced by the scattering at the interfaces of the grain boundaries, therefore, the discussion is based mainly on the behavior of the Seebeck coefficient. As shown in Fig.  3(a), the behaviors of the Seebeck coefficients of the SBN61Ar and SBN61H1100 samples can be divided into three parts: part I is in the low temperature range (below 380  K for SBN61Ar, and below 400  K for SBN61H1100); part II is in the middle temperature range (380  K∼ 508  K for SBN61Ar, and 400  K∼ 508  K for SBN61H1100); and part III is in the high temperature range (above 508  K for SBN61H1100 and SBN61Ar). The behavior of the Seebeck coefficient of the SBN61H1250 sample can be divided into two parts at temperature 457  K.

Firstly, we discuss the slightly reduced samples SBN61Ar and SBN61H1100. For these two samples, their temperature ranges are divided into three parts. In part I, the magnitudes of the Seebeck coefficients decrease with the increase of temperature, and the values of ln ρ for the two samples each show a linear dependence on 1/T, as displayed in Fig.  4(a), which indicates a thermal activation behavior. The ρ and S of this behavior can be related by[14]

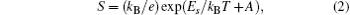
where ρ 0 and A are the constants, kB is the Boltzmann constant, Eρ is the overall activation energy for conduction, and Es is the activation energy associated with carrier generation. If Eρ = Es, the semiconductor gap and the resistivity are thermally activated; however, if Eρ is larger than Es, the behavior is dominated by polaron hopping.[14] In this case, the charge carriers just jump between the neighbouring sites and the hopping is also thermally activated.[14, 15] From the data in Figs.  3(a) and 4(a), the values of Eρ and the Es for sample SBN61Ar and sample SBN61H1100 can be calculated according to Eqs.  (1) and (2): Eρ is about 0.29  eV, and Es is about 0.01  eV. Apparently, Eρ is larger than Es, so the conduction behavior in part I is dominated by the thermal activated polaron hopping.

Part II shows the scenarios of temperature invariant S for the two samples SBN61Ar and SBN61H1100. There is an obvious change for the Seebeck coefficient from part I to part II, and this change may be correlated with the 4mm-to-4/mmm phase transition.[10, 11] In this part, the temperature-independent Seebeck coefficient can be described by the Heikes formula: S = − (kB/e) ln[(2 − c)/c], where c is the ratio of the number of electrons to the number of sites. It indicates that the Seebeck coefficient is determined solely by the constraints on the occupancy of states and the density of electrons in the system. The temperature independence of the Seebeck coefficient is governed entirely by the entropy change per added carrier.[16, 17] At the same time, the electrical resistivity shows an insulating behavior. Considering the complex crystal structure and large disorder in SBN, this behavior is probably due to the Fermi glass behavior, in which the disorder is great enough to ensure that electrons are localized in the Anderson sense.[14]

Fig.  4. Curves of lnρ versus 1000/T (a) and ln ρ versus T− 1/ 4 (b) for samples SBN61Ar, SBN61H1100, and SBN61H1250.

In part III, the magnitudes of the Seebeck coefficient increase steadily with the increase of temperature, and the slope of S versus T plot does not change obviously. The electrical resistivity values of these two samples each show a transition from semiconductor behavior to metal-like behavior at about 770  K. Taking these factors into account, these transport properties are assumed to be dominated by the Anderson localized behavior in a conduction band. Therefore, the resistivity should follow the variable range hopping (VRH) model at first, and the relation between ρ and T is given by Mott’ s law[18]

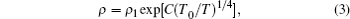
where ρ 1 and C are the constants and T0 is the Mott characteristic temperature. As shown in Fig.  4(b), the ln ρ depends linearly on T− 1/4 in the first temperature region in part III, following the VRH model. Then, after the temperature rises above T0, the electrons begin to enter into the extended states, and the variable range hopping turns into the fixed range hopping. Thus, the resistivity is determined mainly by the thermal activation behavior, and the relation of ρ and T obeys the following equation:[18]

where ρ 2 is a constant, and Δ ε = ε c − ε F is the thermal activation energy (ε c is the mobility edge, and ε F is the Fermi level). The ln ρ linearly depending on 1/T above T0 (∼ 594  K for SBN61Ar, 563  K for SBN61H1100) is also shown in Fig.  4(a). Finally, because plenty of electrons enter into the extended states, no more electrons enter into the extended states from the localized states with the increase of temperature. Therefore, the scattering plays an important role in determining the electrical resistivity. In this case, the resistivity should follow the metal-like model: ρ ∼ Tα , where α is an exponent of T.[18] As shown in the inset of Fig.  3(b), above 770  K, the ρ begins to increase with the increase of temperature, indicating the metal-like conduction behavior. Therefore, it could be concluded that the electrical conduction behaviors in part III for SBN61Ar and SBN61H1100 should be dominated by the Anderson localized theory.

In summary, the electrical transport behaviors of SBN61Ar and SBN61H1100 samples are dominated by the thermally-activated polaron hopping in the low temperature range, the Fermi glass behavior in the middle temperature range, and the Anderson localized behavior in the high temperature range. In the low temperature region, the interaction between electrons and the lattice is very strong, and the lattice near electrons is distorted to form the polaron. So the transport behavior is dominated by the thermally-activated polaron hopping. After the phase transition around 400  K, the interaction between electrons and the lattice is weakened and the polaron is broken up. In the intermediate temperature region, the disorder of the lattice is so strong that all electron states are localized, therefore, the transport behaviors exhibit the Fermi glass behaviors. With increasing the temperature, the disorder of the lattice is weakened and the extended states appear after the phase transition at 508  K. Thus the transport behaviors are dominated by the classical Anderson localized conducting band model in the high temperature region.

In most of the heavily oxygen-reduced sample SBN61H1250, the transport behaviors can be divided into two different parts at about 457  K, as shown in Fig.  3(a). Like the discussion above, the thermal-activated polaron hopping behavior is present in the low temperature region and the Anderson localized conducting band behavior appears in the high temperature region. The Fermi glass behavior with the plateau Seebeck coefficient is not observed in the sample SBN61H1250, indicating that the disorder in the lattice should be weakened by oxygen reduced treatment. It is still an open question how the oxygen reduced treatment influences the disorder of the lattice, which needs further investigation, both experimentally and theoretically.

3.3. Thermal conductivity

Figure  5 shows the variations of total thermal conductivity κ (a), and the lattice thermal conductivity κ l (b) with temperature. The value of κ l is calculated by subtracting the electronic thermal conductivity κ e from κ . κ e is calculated by the Wiedemann– Franz relation, κ e = LT/ρ (where L = 2.23 × 10− 8  V2/K2 is the Lorenz number, ρ is electrical resistivity, and T is the absolute temperature).[18] With increasing the oxygen-reduction degree, the average grain size decreases and the NbO2 second phase appears in the heavily reduced sample, both of which can reduce the lattice thermal conductivity. However, the magnitude of the lattice thermal conductivity increases, indicating that the scattering of grain boundaries and NbO2 second phase do not have the largest influence on the lattice thermal conductivity. The increase of the lattice thermal conductivity might be related to the change of the lattice structure, such as weakened disorder. As shown in Fig.  5(b), the values of lattice thermal conductivity of these three samples exhibit the same behaviors. At first, the κ l increases with the increase of temperature. Then, the high-temperature plateau κ l (∼ 1.77  W/Km, 1.97  W/Km, 1.98  W/Km for SBN61Ar, SBN61H1100, and SBN61H1250, respectively) is observed when the temperature is above 530  K. This thermal conduction behavior indicates a glass-like thermal conductivity, which probably relates to the complex lattice structure.[19, 20]

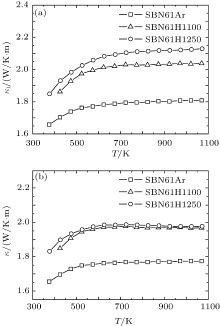Fig.  5. Variations of total thermal conductivity (a) and lattice thermal conductivity (b) with temperature for samples SBN61Ar, SBN61H1100, and SBN61H1250.

However, the magnitude of the glass-like lattice thermal conductivity of SBN61 is surprisingly larger than the one (∼ 1  W/Km) predicted by the method in the literature.[21] The origin of this glass-like thermal conductivity remains to be further investigated.

3.4. Thermoelectric figure of merit

The values of thermoelectric figure of merit (ZT) of SBN61Ar, SBN61H1100, and SBN61H1250 each as a function of temperature are shown in Fig.  6. The ZT values for all the samples increase with the increase of temperature in the measured range. Although, as discussed above, the oxygen-reduction raises the thermal conductivity, the increase of the PF value due to the oxygen-reduction plays a more important role in determining the thermoelectric figure of merit. Therefore, the SBN61 ceramic reduced in a deeper degree obtains a higher ZT value, and the sample SBN61H1250 has the highest ZT value (∼ 0.19 at 1073  K). It can be concluded that the oxygen-reduction for SBN61 is helpful to improving the thermoelectric properties.

Fig.  6. Curves of thermoelectric figure of merit (ZT) with temperature for samples SBN61Ar, SBN61H1100, and SBN61H1250.

4. Conclusions

The thermoelectric properties of Sr0.61Ba0.39Nb2O6− δ ceramics, reduced in different conditions, are investigated in the temperature range from 323  K to 1073  K. In the slightly oxygen-reduced Sr0.61Ba0.39Nb2O6− δ ceramics, at first, the electrical conduction mechanism follows a thermally-activated polaron hopping behavior when the temperature is below 380  K. Then a 4mm-to-4/mmm phase transition appears at 380  K, and the Seebeck coefficient becomes unchanged with temperature, showing the Fermi glass behavior. Above the temperature 508  K, the electrical transport is dominated by the Anderson localized transport behavior in a conduction band. In the most heavily reduced sample, the Fermi glass behavior with a plateau Seebeck coefficient in the middle temperature range disappears. The absolute Seebeck coefficient and the electrical resistivity decrease with deepening the oxygen-reduction degree, resulting in the increasing of the thermoelectric power factor (PF). The values of lattice thermal conductivity of all the reduced SBN61 samples each show a glass-like behavior. Although the thermal conductivity of SBN61 ceramic increases with deepening the oxygen-reduction, the ZT value is dramatically enhanced via the enhancement of thermoelectric power factor. The heaviest oxygen reduced sample SBN61H1250 achieves the highest ZT value of ∼ 0.19 at 1073  K.

Reference
1 Snyder G J, Christensen M, Nishibori E, Caillat T and Iversenet B B 2004 Nat. Mater. 3 458 DOI:10.1038/nmat1154 [Cited within:1] [JCR: 35.749]
2 Svechnikova T E, Shelimova L E, Konstantinov P P, Kretova M A, Avilov E S, Zemskov V S, Stiewe C, Zuber A and Muller E 2005 Inorg. Mater. 10 1043 DOI:10.1007/s10789-005-0258-y [Cited within:1] [JCR: 0.376]
3 Zhang H, Luo J, Zhu H T, Liu Q L, Liang J K, Li J B and Liu G Y 2012 Chin. Phys. B 21 106101 DOI:10.1088/1674-1056/21/10/106101 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
4 Nolas G S, Cohen J L, Slack G A and Schujman S B 1998 Appl. Phys. Lett. 73 178 DOI:10.1063/1.121747 [Cited within:1] [JCR: 3.794]
5 Venkatasubramanian R, Siivola E, Colpitts T and O’Quinn B 2001 Nature 413 597 DOI:10.1038/35098012 [Cited within:1] [JCR: 38.597]
6 Tritt T M 2002 Thermoelectric Materials: Principles, Structure, Properties, and Applications, in: Encyclopedia of Materials: Science and Technology 1 11 [Cited within:1]
7 Lu P X, Qu L B and Cheng Q H 2013 Chin. Phys. B 22 117101 DOI:10.1088/1674-1056/22/11/117101 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
8 H Ohta 2007 Mater. Today 10 44 DOI:10.1016/S1369-7021(07)70207-9 [Cited within:2] [JCR: 6.071]
9 Liu Y, Li H J, Zhang Q, Li Y and Liu H T 2013 Chin. Phys. B 22 057201 DOI:10.1088/1674-1056/22/5/057201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
10 Lee S, Wilke R H T, Trolier-McKinstry S, Zhang S J and Rand all C A 2010 Appl. Phys. Lett. 96 031910 DOI:10.1063/1.3291563 [Cited within:6] [JCR: 3.794]
11 Lee S, Dursun S, Duran C and Rand all C A 2011 J. Mater. Res. 26 26 DOI:10.1557/jmr.2010.78 [Cited within:5] [JCR: 0.691]
12 Choy C L, Leung W P, Xi T G, Fei Y and Shao C F 1992 J. Appl. Phys. 71 70 DOI:10.1063/1.350648 [Cited within:1] [JCR: 0.71]
13 Liu J, Wang C L, Yi L, Su W B, Zhu Y H, Li J C and Mei L M 2013 J. Appl. Phys. 114 223714 DOI:10.1063/1.4847455 [Cited within:1] [JCR: 0.71]
14 Mott N F and Davis E A 1971 Electronic Processes in Non-Crystalline Materials2nd edn. New York Oxford University Press [Cited within:4]
15 Jaime M, Salamon M B, Pettit K, Rubinstein M, Treece R E, Horwitz J S and Chrisey D B 1996 Appl. Phys. Lett. 68 1576 DOI:10.1063/1.116686 [Cited within:1] [JCR: 3.794]
16 Heikes R R and Ure R W 1961 Thermoelectricity: Science and Engineering New York Interscience 77 [Cited within:1]
17 Chaikin PM and Beni G 1976 Phys. Rev. B 13 647 DOI:10.1103/PhysRevB.13.647 [Cited within:1]
18 Kittel C 1996 Introduction to Solid State Physics7th edn. New York John Wiley [Cited within:4]
19 Fischer E, Hässler W and Hegenbarth E 1982 Phys. Stat. Sol. 72 169 DOI:10.1002/(ISSN)1521-396X [Cited within:1]
20 Kittel C 1949 Phys. Rev. 75 972 DOI:10.1103/PhysRev.75.972 [Cited within:1] [JCR: 6.583]
21 Cahill D G, Watson S K and Pohl R O 1992 Phys. Rev. B 46 6131 DOI:10.1103/PhysRevB.46.6131 [Cited within:1]