†Corresponding author. E-mail: lifeipaper@163.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11204076 and 11147011), the Scientific Research Fund of Hunan First Normal University (Grant No. XYS13N16), and the Opening Project of Key Laboratory of Low-dimensional Quantum Structures and Quantum Control (Hunan Normal University), Ministry of Education (Grant No. QSQC1005).
A space-dependent atomic superfluid current with an explicit analytical expression and its role in Bose–Einstein condensates are studied. The factors determining the intensity and oscillating amplitude of the space-dependent atomic superfluid current are explored in detail. Research findings reveal that the intensity of the current can be regulated by setting an appropriate configuration of the trap and its oscillating amplitude can be adjusted via Feshbach resonance. It is numerically demonstrated that the space-dependent atomic superfluid current can exert great influence on the spatial distribution of condensed atoms, and even force condensed atoms into very complex distributional states with spatial chaos.
In 1941 Landau first introduced the term superfluidity to describe the amazing properties of superfluid helium.[1] To date, it has been recognized that Bose– Einstein condensates (BECs) are idealized models for superfluid.[2] It may help to understand the meaning of superfluidity. In recent years, phenomenological features of superfluidity in gaseous BECs have been experimentally examined.[3– 9] The observation of the scissors mode of a 87Rb BEC gives direct evidence of superfluidity in BECs.[3] For impurity atoms propagating through a trapped BEC, the collisional cross section is dramatically reduced when the impurity velocity is reduced below the condensate speed of sound.[4] This is in good agreement with the Landau criterion for superfluidity.[1] A recent experiment with resonantly pumped polariton condensates demonstrated superfluidity as a dramatic reduction in the intensity of resonant Rayleigh scattering, [5] just as originally predicted in Ref. [6]. At present, one of the most concerned superfluid phenomena in the BEC field is the vortex. Using a focused laser beam to stir a single component BEC of 87Rb, Madison et al. observed the formation of a vortex.[7] Vortex fusion and giant vortex states in confined superconducting condensates have been observed.[8] The vortice in two-component BECs was created through a coherent process involving the spatial and temporal control of interconversion between the two components.[9] Stimulated by experimental findings, there has always been a great deal of effort devoted to theoretical studies on the superfluid in BECs.[10– 22] The superfluidity of a BEC with periodically modulated scattering length has been studied theoretically and when the modulation strength is strong enough, the BEC loses its superfluidity completely.[17] With a theoretical technique Yan and coworkers studied two-dimensional superfluid flows in inhomogeneous BECs.[18] The existence of superfluidity in a driven-dissipative Bose gas out of thermal equilibrium was revealed and the relation with conventional superfluids was discussed theoretically.[19] In addition to single superfluids, miscible superfluids in BECs also attract research attention.[20]
Undoubtedly, the superfluids can exert significant influence on BECs, and may even result in chaotic behaviors in the system. It has been reported that for some specific parameters and initial/boundary conditions, spatial chaos[23– 28] and dynamical chaos[29– 41] can appear in BECs. Due to the diversity of the configurations of BEC systems, there are still open problems to be considered. This is the aim of the present work.
We start from the quasi-one-dimensional (1D) mean-field Gross– Pitaevskii equation (GPE)
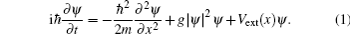
At zero temperature in the lowest-order mean-field approximation, the dynamical evolution of BEC in a cigar-shaped trap can be well described by the above equation. Here ψ = ψ (x, t) is the macroscopic quantum wave function of the quasi-1D BEC, ħ is Planck’ s constant, m is the atomic mass, Vext(x) is a 1D trapping potential, g = 2ħ ω ⊥ as characterizes the interatomic interaction strength with ω ⊥ and as the frequency of atomic oscillations in the radial direction and the s-wave scattering length, respectively. as > 0 indicates a repulsive interaction and as < 0 corresponds to an attractive case.
In the early years, manipulations of BECs were often by means of modulating the external trapping potentials.[42, 43] Afterwards, an advanced experimental technique called Feshbach resonance made it possible to rapidly and effectively adjust the value and sign of the s-wave scattering length at will.[44– 50] That means the value and sign of the nonlinear parameter can also be rapidly and effectively adjusted accordingly through the Feshbach resonance technique. A varying scattering length can be achieved in a very broad range by employing either magnetic or optical Feshbach resonances and undoubtedly can become an effective tool for manipulations of BECs.[51] Time-dependent s-wave scattering lengths are first realized and widely used in a variety of manipulations of BECs in experiments.[52– 54]
In recent years, the experimental realization and role of space-dependent s-wave scattering lengths in BEC systems has aroused more and more interest.[45– 47, 54] It has been reported that space-dependent scattering lengths can be achieved by a (longitudinally) changing transversal confinement or an inhomogeneity of the external magnetic field in the vicinity of a Feshbach resonance.[55] Consequently, a space-dependent nonlinear parameter can be obtained. Owing to this, in this paper we will consider a space-dependent nonlinear parameter bearing the following form[45, 46]

where g0 is the nonlinear parameter in absence of modulation and g1 is the amplitude of the modulation. κ is the wave number of the modulating laser. For simplicity, we adopt the dimensionless variables as given below

with n being the number density of BEC atoms and [κ ] the unit of κ . It will not cause misunderstanding to remove “ ∼ ” from the above variables. Then the quasi-1D GPE can be rewritten in the following dimensionless form

Applying the transformation 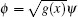
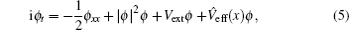

Considering a weak scattering-length modulation satisfying g0 ≫ g1 and substituting Eq. (2) into Eq. (6) yields
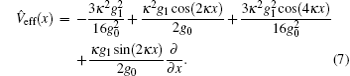
Due to the constraint condition g0 ≫ g1, we can define a small quantity ε = κ g1/g0 ≪ 1, which leads to
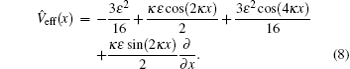
In order to get a better understanding of BEC dynamics, we assume the solution of Eq. (5) to be the time-dependent variational macroscopic condensate wave function of the form

where μ denotes the chemical potential of BEC, proportional to the number of atoms trapped in the condensate, R(x) and θ (x) are the amplitude and the phase of the wave function, respectively. Both R(x) and θ (x) are real functions. Inserting Eq. (9) into Eq. (5), we obtain the following two coupled nonlinear ordinary differential equations


with 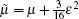

Integrating Eq. (12) over the space coordinate, we obtain an interesting result as

From the above expression, one can see that its left side is a product of R2 and dθ /dx. R2 is proportional to the number density of BEC atoms and dθ /dx is the superfluid velocity field. Therefore, equation (13) clearly implies that there exists a space-dependent atomic superfluid current
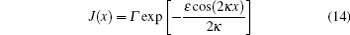
in the system. Here Γ is an integral constant determined by boundary conditions. ε has been defined as a small quantity before, leading to e− ε cos(2κ x)/2κ ≈ 1. Therefore Γ overwhelmingly determines the intensity of the space-dependent atomic superfluid current. That means in experiments the intensity of the atomic superfluid current can be controlled by setting appropriate boundary conditions, because the boundary conditions are directly relevant to the trap potential. Therefore, the intensity of the superfluid current is closely and directly attached with the trap potential. Below we will demonstrate that the oscillating amplitude of the superfluid current can be tuned through the Feshbach resonance.
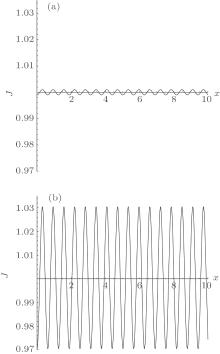
Due to ε = κ g1/g0, evidently, the explicit analytical expression (14) contains the parameters κ , g0, and g1, which indicates that the atomic superfluid current can be adjusted through Feshbach resonance. From Eq. (14) we numerically demonstrate the space-dependent superfluid current in Fig. 1 with Γ = 1, κ = 5, and different values of ε . In Fig. 1(a) one can observe that the oscillating amplitude of the superfluid current is small when ε = 0.01. Keeping the values of Γ and κ fixed and increasing ε to 0.3, we see a much larger oscillating amplitude of the superfluid current in Fig. 1(b). According to Fig. 1 and the above discussion, we know the oscillating amplitude of the superfluid current can be regulated through the Feshbach resonance and the superfluid current always oscillates near “ 1” almost symmetrically, showing that the average intensity of the superfluid current is approximately equal to “ 1” . In plotting Fig. 1 we have set Γ = 1, therefore, figure 1 just shows the spatial evolution of e− ε cos(2κ x)/2κ . So when condition ε = κ g1/g0 ≪ 1 is strictly satisfied, the average value of the intensity of the superfluid current will be approximately equal to the value of Γ . Thus, one can reach such a conclusion that the boundary conditions will overwhelmingly determine the average intensity of the space-dependent atomic superfluid current. Undoubtedly, the atomic superfluid current and its oscillating amplitude can exert an important effect on the dynamical evolution of BECs. Studies of the atomic superfluid current will help to manipulate BECs.
Applying Eqs. (13) and (14) to Eq. (10), we obtain

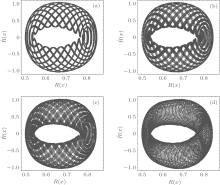
In order to investigate the influence of the space-dependent atomic superfluid current on the spatial distribution of BEC atoms, we first consider Vext as a typical harmonic potential of the dimensional form mω ̃ 2x2/2 whose dimensionless form is ω 2x2/2 with ω = m2ω ̃ 2/[κ ]4ħ 2. Here ω ̃ is the trap frequency of the harmonic potential and ω is the corresponding dimensionless trap frequency. After applying ω 2x2/2 to Eq. (15) and numerically calculating it, we picture the phase orbits on the equivalent phase space (R, Ṙ ) in Fig. 2 with the “ MATHEMATICA” soft package. The values of Γ , κ , and ε for Figs. 2(a) and 2(b) are the same as those of Figs. 1(a) and 1(b), respectively. The other parameters and boundary conditions are set as μ ̃ = 10.1, ω = 0.001, R(0) = 0.5, and Ṙ (0) = 0. Figure 1(a) has shown that when ε = 0.01, the oscillating amplitude of the superfluid current is small, and from the corresponding phase space in Fig. 2(a), we can see only one closed orbit. That means for a superfluid current with a small oscillating amplitude BEC atoms are in a regular state with a single-periodic spatial distribution. For a superfluid current with a larger oscillating amplitude as shown in Fig. 1(b), the phase portrait in Fig. 2(b) demonstrates that great change occurs and a lot of phase orbits interweave with each other forming a typical quasi-period phase space, implying BEC atoms in a spatial quasi-period state.
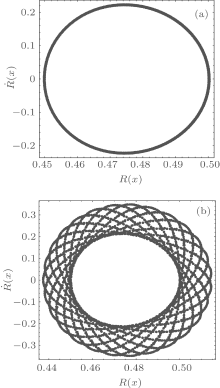 | Fig. 2. Plots of the orbits in the equivalent phase space (R, Ṙ ) with μ ̃ = 10.1, ω = 0.001, R(0) = 0.5, Ṙ (0) = 0. (a) ε = 0.01, (b) ε = 0.3. |
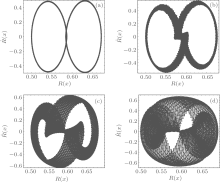
To further confirm the effect of the atomic superfluid current on the BEC system, we select a typical optical lattice potential of the form V cos(2Kx) as the trapping potential Vext. It will not result in misleading to treat V cos(2Kx) as a dimensionless one. We set the parameters and boundary conditions as μ ̃ = 3.17, K = 7, V = 3.52, R(0) = 0.5, Ṙ (0) = 0 and plot the equivalent phase space (R, Ṙ ) in Fig. 3. The values of Γ , κ , and ε for Figs. 3 (a) and 3(b) are the same as those of Figs. 1(a) and 1(b), respectively. For the small oscillating amplitude with ε = 0.01, a typical quasi-period phase portrait appears in the phase space of Fig. 3(a), clearly denoting that BEC atoms are in a spatial quasi-period distributional structure. For the large oscillating amplitude with ε = 0.3, one cannot distinguish the number of the phase orbits and the phase space structure due to the complexity of the phase space, as can be seen in Fig. 3(b). This implies that BEC atoms are in a complex or even chaotic spatial distribution.
 | Fig. 3. Plots of the orbits in the equivalent phase space (R, Ṙ ) with μ ̃ = 3.17, K = 7, V = 3.52, R(0) = 0.5, Ṙ (0) = 0. (a) ε = 0.01, (b) ε = 0.3. |
Through comparing Fig. 3 with Fig. 2, one can conclude that a space-dependent atomic superfluid current with large oscillating amplitude can dramatically influence the spatial distribution of BEC atoms. In fact, due to ε = κ g1/g0, for a fixed κ , changing ε is equivalent to changing the ratio g1/g0. A small ε means a small value of g1/g0, namely a small parametrical modulation of the nonlinear interaction between BEC atoms; on the contrary, a large ε means a strong parametrical modulation of the nonlinear interaction between BEC atoms. It is just the parametrically modulating intensity of the nonlinear interaction between BEC atoms that actually determines the oscillation intensity of the atomic superfluid current. As a result, an atomic superfluid current with a large oscillating amplitude represents a stong parametrical modulation of the nonlinear interaction between BEC atoms, which will undoubtedly result in an apparent change in the spatial distribution of BEC atoms, and even forces BEC atoms into a chaotic spatial distribution.
In further numerical simulations for the same parameters and initial conditions as those of Figs. 2 and 3 respectively, we find that when the trapping potential is a typical harmonic potential, in the range 0 ≤ ε ≤ 0.3 the system is always in a series of quasi-periodic states similar to the one represented by Fig. 3(a); when the trapping potential is a typical optical lattice potential, in the range 0 ≤ ε < 0.07 the system is also in a series of quasi-periodic states; but when 0.07 ≤ ε ≤ 0.3, the system exhibits a series of chaotic states. In Fig. 4 we plot the phase portraits for ε = 0, 0.02, 0.04, 0.07 and the other parameters and initial conditions are the same as those in Fig. 3. Figures 4(a)– 4(c) demonstrate visible quasi-periodic orbits in the phase spaces. But when ε increases to 0.07, all quasi-periodic features vanish and a typical chaotic phase portrait appears, see Fig. 4(d). That indicates 0.07 may be the critical value of ε in the range 0 ≤ ε ≤ 0.3 for avoiding or producing spatial chaos under the selected parameters and initial conditions. The parameter κ is coupled with ε through ε = κ g1/g0. We have discussed the critical value of ε for avoiding or producing spatial chaos, so it is not necessary to do the same on κ .
In this paragraph, we explore the effect of Γ on the BEC system. We adjust the value of Γ and keep the other parameters and boundary conditions the same as those of Fig. 3(a). It is found that when Γ = 0.8085, two closed orbits appear in the phase space of Fig. 5(a) implying that the system is in a biperiodic spatial structure. When the value of Γ is changed to 0.812, multi-periodic phase orbits appear in the phase space of Fig. 5(b), which indicates that the BEC atoms are in a multi-periodic spatial distributional state. When Γ keeps increasing to 0.82, the phase orbits in Fig. 5(c) show that the system enters into a complex state with some chaotic characteristics. Finally, when Γ = 0.83, a typical chaotic attractor appearing in the phase space of Fig. 5(d) clearly illustrates that BEC atoms are in a chaotic spatial distributional state. The evolution of the phase portraits in Fig. 5 demonstrates that when Γ increases from 0.8085 to 0.83, BEC atoms undergo a process from a regular biperiodic spatial distribution to a chaotic spatial distribution under the selected parameters and boundary conditions.
The above discussion shows that adjusting some specific parameters relevant to the space-dependent superfluid current can cause spatial chaos. So in experiments these parameters can be chosen as controlling ones to avoid or produce spatial chaos.
In summary, we have studied the space-dependent atomic superfluid current and discussed its role in the spatial distribution of BEC atoms. Research findings demonstrate that the oscillating amplitude of the atomic superfluid current can be adjusted through Feshbach resonance and the intensity of the superfluid current can be controlled by setting appropriate boundary conditions. Numerical simulations for cases with typical trapping potentials reveal that the atomic superfluid current can dramatically influence the spatial distribution of the BEC atoms, and even force the system into very chaotic spatial distributional structures. It is undeniable that the spatial distributional structure of BEC atoms plays a crucial role in the BEC dynamics. As a result, studies on the spatial distribution of BEC atoms are of great importance in the BEC field.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|