Cite this Article
Yu Bin, Deng Jian-Hua, Wang Zheng, Li Bao-Hui, Shi An-Chang. Self-assembly of lamella-forming diblock copolymers confined in nanochannels: Effect of confinement geometry* . Chinese Physics B, 2015, 24(4): 046402  
Permissions
Self-assembly of lamella-forming diblock copolymers confined in nanochannels: Effect of confinement geometry*
Yu Bina)†, Deng Jian-Huaa), Wang Zhengb), Li Bao-Huib)‡, Shi An-Changc)
Department of Physics and Materials Science, Tianjin Normal University, Tianjin 300387, China
Department of Physics and Astronomy, McMaster University, Hamilton, Ontario L8S 4M1, Canada
School of Physics, Key Laboratory of Functional Polymer Materials, Ministry of Education, Nankai University, and Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), Tianjin 300071, China

†Corresponding author. E-mail: stevenyubin@163.com

‡Corresponding author. E-mail: baohui@nankai.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11204215, 51302187, 20990234, 20925414, 21204040, and 91227121), the Natural Science Foundation of Tianjin City, China (Grant Nos. 12JCYBJC32500 and 14JCZDJC32100), the Program for Changjiang Scholars and Innovative Research Team in University (PCSIRT) (Grant No. IRT1257), and the 111 Project. A. C. Shi gratefully acknowledges the supports from the Natural Sciences and Engineering Research Council (NSERC) of Canada.

Abstract

The self-assembly of symmetric diblock copolymers confined in the channels of variously shaped cross sections (regular triangles, squares, and ellipses) is investigated using a simulated annealing technique. In the bulk, the studied symmetric diblock copolymers form a lamellar structure with period LL. The geometry and surface property of the confining channels have a large effect on the self-assembled structures and the orientation of the lamellar structures. Stacked perpendicular lamellae with period LL are observed for neutral surfaces regardless of the channel shape and size, but each lamella is in the shape of the corresponding channel's cross section. In the case of triangle-shaped cross sections, stacked parallel lamellae are the majority morphologies for weakly selective surfaces, while morphologies including a triangular-prism-shaped B-cylinder and multiple tridentate lamellae are obtained for strongly selective surfaces. In the cases of square-shaped and ellipse-shaped cross sections, concentric lamellae are the signature morphology for strongly selective surfaces, whereas for weakly selective surfaces, stacked parallel lamellae, and several types of folding lamellae are obtained in the case of square-shaped cross sections, and stacked parallel lamellae are the majority morphologies in the case of ellipse-shaped cross sections when the length of the minor axis is commensurate with the bulk lamellar period. The mean-square end-to-end distance, the average contact number between different species and the surface concentration of the A-monomers are computed to elucidate the mechanisms of the formation of the different morphologies. It is found that the resulting morphology is a consequence of competition among the chain stretching, interfacial energy, and surface energy. Our results suggest that the self-assembled morphology and the orientation of lamellae can be manipulated by the shape, the size, and the surface property of the confining channels.

Keyword: 64.75.Jk; 64.75.Yz; 83.80.Uv; 83.80.Sg; diblock copolymers; self-assembly; confinement geometry; phase behavior
1. Introduction

The self-assembly of block copolymers has attracted tremendous scientific attention due to the formation of various equilibrium ordered structures and the potential applications of these structures in nano-technology.[1] Potential applications of block copolymer microstructures include lithographic templates for nano-arrays, [2] nanodots, and nanoholes in metal films, [3] photonic crystals, [4] etc. For the simplest diblock copolymers, ordered bulk phases including body-centered-cubic arrays of spheres, hexagonally packed cylinders, lamellae and a bicontinuous network structure called gyroid have been identified experimentally[5] and theoretically.[6, 7] In a spatially confined environment, the combination of the structural frustration, confinement-induced entropy loss, and wall interactions provides opportunities to engineer novel structures which cannot be obtained in the bulk.

The self-assembly of diblock copolymers under one-dimensional (1D) confinement, where the block copolymers are sandwiched between two parallel surfaces forming polymer thin films, has been well studied.[8– 15] For bulk lamella-forming symmetric diblock copolymers, much attention has been focused on controlling the orientation of the lamellae with respect to the confining surfaces. The existing research illustrates that lamellar structures perpendicular to the surfaces (perpendicular lamellae) are preferred when the surfaces are neutral. As the surface preference to one of the two blocks is strong enough, lamellae parallel to the surfaces (parallel lamellae) are the preferred structures. However, when the surface preference is weak, either perpendicular or parallel lamellae are observed, depending on the commensurability between the film thickness and the bulk period LL.[14] When the film thickness is commensurate with LL, parallel lamellae are preferred. On the other hand, perpendicular lamellae are formed when the film thickness is incommensurate with LL. Furthermore, it is found that the lamellar period of parallel lamellae oscillates around LL with changing the film thickness.[14, 15] In general, the interplay between the confinement and the strength of surface preference causes morphological deviations from that observed in the bulk for asymmetric diblock copolymers.[11– 13] The self-assembly of a mixture of diblock copolymers confined between two parallel walls has also been investigated.[16]

In recent years, the self-assembly of diblock copolymers under two-dimensional (2D) confinement imposed by using nano-channels has aroused significant interest. It has been demonstrated that 2D confinement can lead to richer morphologies due to the very tightly confined geometry compared with 1D confinement.[17– 41] The interplay of symmetries of block copolymers and confining geometries, the principles of complex structure formation from confined block copolymers, and the relationship between the confining conditions and the resulting structures for diblock copolymers under 2D and three-dimensional (3D) confinements have been reviewed.[42– 44] In experiments, the phase behaviors of polystyrene-b-polybutadience (PS-b-PBD) diblock copolymers confined in cylindrical nanochannels of alumina membranes were studied.[17– 21] The diameter of the cylindrical channels (D) varies from tens of nm to more than one hundred nm. For symmetric diblock copolymers, concentric lamellar structures are obtained when the channel diameter D is several times the bulk period LL due to the preferential interaction of the channel wall for one block. When D is comparable to LL and D/LL is not an integer, novel morphologies such as stacked-disks or toroids are observed experimentally.[18] Concentric lamellae were also observed by Sun et al. in their study of symmetric polystyrene-b-poly(methyl methacrylate) diblock copolymers confined in alumina nanochannels, [22] and by Ma et al. in their studies of polystyrene-b-polyisoprene nanowires[23] and of polystyrene-b-polydimethylsiloxane nanofibers[24] fabricated by confining block copolymers in a cylindrical poly(methacrylic acid) shell using an electrospinning technique. The self-assembly of diblock copolymers in 2D confinement has also been extensively investigated by theoretical and simulation studies.[25– 37] He et al.[25] and Sevink et al.[26] investigated the morphologies of bulk lamella-forming diblock copolymers confined in cylindrical channels using Monte Carlo and dynamical density functional simulations, respectively. For channels with strongly selective surfaces for one of the blocks, concentric lamellae were observed.[25, 26] Lamellae normal to the channel axis (perpendicular lamellae) were observed when the surface is neutral to both of the blocks.[26] Concentric lamellar structures have also been predicted by Li et al. using self-consistent field theory calculations in 2D for diblock copolymers under cylindrical confinement.[28] In subsequent extensive studies, the effects of the surface field are systematically investigated. The combination of the surface preference and the structural frustration due to being incommensurate between D and LL can lead to other novel morphologies, such as porous lamellar morphologies, stacked lamellae parallel to the channel axis (stacked parallel lamellae), as well as helices besides the concentric and perpendicular lamellae for bulk lamella-forming diblock copolymers confined in cylindrical channels as shown in Monte Carlo[29, 30, 33– 35] and dissipative particle dynamics[35] (DPD) simulations. Besides the equilibrium morphologies, a variation of layer thickness with the channel diameter in concentric lamellar structures was also reported.[28– 30] Furthermore, the surface-induced effects on the morphologies of lamella-forming diblock copolymers in nanorod arrays have also been studied.[45]

Comparing the self-assembled morphologies of lamella-forming diblock copolymers in 2D cylindrical confinement with those observed in 1D confinement, it is apparent that the perpendicular lamellae and concentric lamellae in 2D confined systems are the counterparts of perpendicular and parallel lamellae, respectively, in 1D confined systems. Furthermore, stacked parallel lamellae and multiple non-lamellar structures are obtained for diblock copolymers under 2D confinement of a cylindrical channel with weakly preferential surfaces.[29, 34] Among these structures, it is interesting and useful to observe that the orientation of stacked parallel lamellae can be controlled by simply tuning the selectivity of the channel-wall. However, in the study of self-assembly of diblock copolymers under cylindrical channels, it was found that the stacked parallel lamellae only occur in a narrow range of channel-wall selectivity and channel size.[29, 34] Thus it may be difficult to observe these structures experimentally. Therefore, it remains a challenge to expand the parameter space in which stacked parallel lamellae are stable.

Meanwhile, the self-assembly of asymmetric cylinder-forming diblock copolymers under the two-dimensional (2D) confinement of the cylindrical channels has been extensively studied.[17, 18, 20, 28, 29, 31, 35, 36, 38– 41] Xiang et al. observed that large channels (D/LL > 4.1) lead to hexagonally packed cylindrical domains.[20] In addition, helical structures have been observed in channels of small diameter (D/LL = 1.1– 1.5).[17] Helices and stacked toroids have been predicted[29, 31, 35, 36, 38– 40] in theory and simulations and confirmed experimentally[21, 41] to spontaneously form for cylinder-forming diblock copolymers inside cylindrical channels. The self-assembled morphologies of a mixture of AB-diblock copolymer and C-homopolymer in nanorod arrays have also been investigated.[46] Interestingly, helices and core-shelled structures were predicted to spontaneously form by the encapsulation of the graphene nanoribbons[47] or carbon nanorings[48] into single-wall carbon nanotube, or by the self-assembly of graphene and metallic particles.[49] The spiral configuration of the graphene nanoribbons[47] or carbon nanorings[48] takes the least amount of energy and achieves the maximum occupancy.

In the present paper, we report a systematic investigation of the self-assembly of lamella-forming diblock copolymers confined in channels of various shaped cross sections. Our study is motivated by the following observations. First of all, for two-dimensionally confined block copolymer systems, most, if not all, of the experiments have been carried out with pores of noncircular cross sections. Furthermore, it has found that the geometry and size of the confining channels have a large effect on the structure and symmetry of the self-assembled morphologies for cylinder-forming diblock copolymers.[18] Secondly, experimental studies of block copolymers confined in channels with regular and non-circular cross sections have been carried out. For example, the self-assembly of sphere-forming diblock copolymers confined in V-shaped[50, 51] grooves, i.e., channels of triangular cross sections, has been investigated.[50, 51] It is found that the V-shaped groove promotes the formation of a well-ordered fcc close-packed sphere array with the (111) planes of the array parallel to the groove walls, which are different from those observed in bulk or in cylindrical confinement. And the sphere size in the block copolymer adjusts, depending on the commensurability between the periodicity of the block copolymer and the film thickness within the V-shaped groove.[51] Finally, the self-assemblies of cylinder-forming diblock copolymers confined in various shaped channels, [39, 52] sphere-forming diblock copolymers confined in square-shaped channels, [53] and lamella-forming diblock copolymers on sparsely nanopatterned substrates[54] as well as in parallel substrates filled with square-pillar arrays, [55] have been systematically investigated theoretically or with simulation. A variety of nanostructures not available in bulk were observed. Based on these existing studies, it is expected that the shape of the confining geometry may have a large effect on the self-assembly of lamella-forming diblock copolymers.

In the present paper, the cross sections of the confining channels include regular triangles, squares, and ellipses. In the bulk, the studied symmetric diblock copolymers form a lamellar structure with period LL. It is found that the geometry and surface property of the confining channel have a large effect on the self-assembled structure and the orientation of the lamellar structure. Morphologies such as stacked perpendicular lamellae, stacked parallel lamellae, multiple tridentate lamellae, and several types of folding lamellae are obtained, depending on the channel shape, size, and surface property. The mean-square end-to-end distance and the average contact number between different monomers are computed to elucidate the formation mechanisms of the different morphologies.

2. Model and method

Our simulation is based on the simulated annealing method applied to the “ single-site bond fluctuation” model of polymers.[56– 58] The simulated annealing is a well-established procedure for obtaining the lowest energy “ ground states” of disordered systems.[59– 62] Our extensive previous studies have established that the simulated annealing and the lattice model are appropriate for studying the self-assembly of block copolymers in confinement.[27, 29, 38, 39] For completeness, the model and algorithm are reviewed briefly below.

Specifically, a diblock copolymer A6B6 is considered in this study. For this symmetric diblock copolymer with fA = 1/2, it has been found that it forms a lamellar phase with period LL = 9.33 in the bulk.[29] In the present study, this lamella-forming diblock copolymer is confined in a long channel of various shaped cross sections. The shapes of the channel cross sections used in this study include regular triangles, squares, and ellipses. For a channel with a regular triangle- or a square-shaped cross section, its size is represented by a characteristic length Dn (n = 3, 4) which is related to the side length of the corresponding regular polygon. For ellipse-shaped channels, we need two characteristic sizes, Dex and Dey, to represent the lengths of two axes in the x and y directions.

The simulations are performed on a model system that is embedded in a simple cubic lattice of volume V = LX × LY × LZ. The lengths of LX and Ly are related to the characteristic lengths of a given channel. In all cases, the extra m with m = 2 is added to construct the channel. That is, Lx = m + D3 and 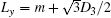for a regular triangle-shaped channel, Lx = Ly = m + D4 for a square-shaped channel, and Lx = m + Dex and Ly = m + Dey for an ellipse-shaped channel. For a given channel, its boundary is constructed by computing and judging the distance of each lattice site to the symmetric axis of the channel cross section based on simple geometric relations. These sites inside the boundary determine the channel and can be occupied by copolymers and vacancies. Each monomer occupies one lattice site and the polymers are self- and mutual-avoiding. The bond lengths are set to be 1 and lattice spacing respectively, so that each site has 18 nearest-neighbor sites. The total monomer concentration in the system is kept at a constant ρ = 85% . The lattice sites outside the channel constitute the channel-wall which cannot be occupied by the polymers. Periodic boundary conditions are adopted in the z direction along the channel. The channel length is set to be LZ = 37 (LZ/LL≈ 4), which has been proven to be the optimum condition.

In all cases, only nearest-neighbor interactions are considered. The repulsive interaction between different kinds of monomers is modeled by parameter ε AB = 1.0kBTref, where kB is the Boltzmann constant and Tref is the reference temperature. The A– A and B– B interactions are set to be zero and interaction between a monomer and a vacancy is also set to be zero. The surface preferences (characterized by the polymer-wall interactions, ε AS and ε BS) are set as − ε AS = ε BS = α ε AB, thus the surface of the channel is strongly selective to the A blocks. For regular triangle- and square-shaped channels, α is varied from 0 to 1 with a small step. For ellipse-shaped channels, the cases with α = 0, 0.1 and 1 are studied.

The start configuration is generated by putting an array of polymer chains onto the lattice inside the channel. The polymer chains are parallel to the z direction along the channel. These chains are either in an extended or one-fold conformation. Starting from the initial state, the ground state of the system is obtained by executing a set of Monte Carlo simulations at reducing temperatures. Simulations with several different random number generator seeds have been performed to test the robustness of the observed self-assembled morphologies. Good reproducibility of the morphologies is obtained. In the following section, self-assembled morphologies are plotted in terms of the densities of A (ρ A) and B (ρ B) blocks on each lattice site. Unless otherwise specified, the curved surfaces with ρ A = 0.5 and ρ B = 0.5 are plotted using the Mayavi software. To render the morphologies smooth, ρ i is defined as ρ i = Ni/Nnnn, where Ni and Nnnn are the numbers of i-monomers (i = A or B) in the nearest-neighbor sites of the given site and of the total nearest-neighbor sites, respectively.

3. Results and discussion
3.1. Channels with regular triangle-shaped cross sections

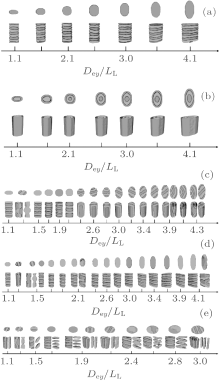
In this case, typical self-assembled morphologies formed with the variations of channel size D3/LL and surface selectivity α , are shown in Fig.  1 where the A-blocks are shown in red and the B-blocks in green. As shown in Fig.  1, morphologies are relatively simple for the limiting cases of α = 1 and α = 0. In the limiting case of α = 1, the channel surfaces are strongly selective to the A-blocks. A wetting A-layer is formed near the channel wall, and the layer presents a shape of the boundary. Inside the wetting A-layer, the structure formed by the B-blocks depends on the channel size. For a small channel with D3/LL ≤ 1.2, a B-cylinder with a roughly circle cross section along the channel is formed. With the increase of the channel size, the cylinder gradually evolves into a triangular-prism-shaped B-cylinder at D3/LL ≈ 1.5 ∼ 2.4. When D3/LL ≈ 2.6, the triangular-prism-shaped cylinder evolves into a morphology of tridentate lamellae where each branched lamella points to each vertex point and is perpendicular to the corresponding side of the triangle. With widening the channel to D3/LL ≈ 3.7, holes occur in the center of the tridentate lamellae and they are filled with A-blocks. With the further increase of the channel size to D3/LL ≈ 3.9, a structure with the B-domain is similar to that obtained at D3/LL ≈ 1.5 ∼ 2.4 but a new A-cylinder with a circular cross section is formed in the center of the channel. It is noticed that the tridentate lamellae occur in a wider range of α (0.3 ≤ α ≤ 1.0) for larger channels with D3/LL > 2.0 whereas they occur in a narrower α range for smaller channels with D3/LL < 2.0. The morphologies with α ≈ 1 in Fig.  1 are different from and much more complex than those obtained for the same block copolymer confined in cylindrical channels, where only concentric-lamellae are observed.[29]

Fig.  1. Self-assembled morphologies formed with the variations of D3/LL and α for symmetric diblock copolymers confined in channels with regular triangle-shaped cross sections. For clarify, the structure of the B domain is also shown for some special morphologies. When the same type of morphology is formed at a given D3/LL but in a range of α values, only these morphologies at the two boundary α values are shown. The color scheme in this and the following figures: A blocks (red) and B blocks (green).

In the limiting case of α = 0, the surfaces are neutral to both A- and B-blocks. Stacked perpendicular lamellae are obtained regardless of D3/LL. It is noticed that the shape of each lamella in a stacked perpendicular lamellar structure is a regular triangle in accordance with the shape of the confinement boundary, and the period of lamellae is the same as LL. It is also noticed that the stacked perpendicular lamellae only occur in the case of neutral surfaces, which is different from that observed for the same diblock copolymer confined in a cylindrical channel where perpendicular lamellae also occur for weakly selective channels.[29, 34]

In contrast to the two limiting cases, complex morphologies are observed for weakly selective surfaces with α = 0.1 ∼ 0.25. At α = 0.1, the typical morphologies can be classified into three categories. The first category consists of a twisted B-cylinder (with D3/LL ≈ 1.2 ∼ 1.7), the second category consists of deformed perpendicular B-lamellae with a period much larger than LL (with D3/LL ≈ 1.0, 2.0, 2.4, 3.5) where the lateral size of each B-lamella is slightly smaller than that of the cross section, and the third category consists of disordered structures (with D3/LL ≈ 2.2, 2.6 ∼ 3.3, 3.7 ∼ 4.1). These frustrated structures reflect the competition between the confinement and the surface selectivity. In a range of α = 0.15 ∼ 0.2, it is interesting to notice that the stacked parallel lamellae are the majority morphologies where the number of A– B interfaces in a structure increases with D/LL. For these stacked parallel lamellae, an A-rich layer always forms on one side surface of the channel due to the A-selectivity of the surfaces, and alternative B- and A-rich layers fill the remaining space of the channel. Therefore, alternative stripes of A and B domains are present on the other two side surfaces of the channel as shown in Fig.  1. It is interesting to notice that a transition of the number of B-rich layers from n to n+ 1 occurs when D3/LL is slightly larger than an integer. The frustrated morphology observed at D3/LL≈ 2.2 and α = 0.15 can be regarded as an intermediate state in the transition process. As shown in Fig.  1, the frustrated morphology evolves into one B-rich layer plus a ring of B-spheres at D3/LL ≈ 2.2 and α = 0.2, and into two B-rich layers at D3/LL ≈ 2.4 and α = 0.15. When α increases to 0.25, the observed morphologies are similar to those obtained in the case with α = 1, except some B-blocks that contact the surfaces.

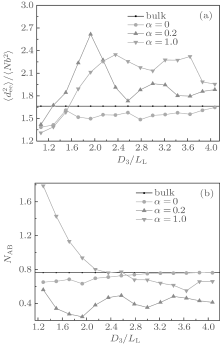
In order to gain an insight into the effects of the chain stretching and interfacial energy on the self-assembled morphology and morphological transition, we compute the mean-square end-to-end distance of chains and the average contact number between each A-monomer and B-monomer, NAB. Figure  2(a) shows the variations of with D3/LL for three typical surfaces, and as a comparison, the bulk value is also plotted in the figure. For neutral surface (α = 0), it is noticed that chains are always slightly compressed with respect to the bulk chains, and approaches to the bulk value with the increase of D3/LL. This result is similar to that in the case when the same copolymer is confined in cylindrical channels.[28] For a weakly selective surface with α = 0.2, is smaller than the bulk value for small channels with D3/LL < 1.2 and is always larger than the bulk value for larger channels with D3/LL > 1.3. When comparing the curve with the morphology shown in Fig.  1, it is noticed that the chains in the stacked parallel lamellae obtained for weakly selective surfaces are strongly stretched within larger channels. It is also noticed that the curve oscillates as a function of D3/LL. It is interesting to notice that there is a peak in the curve at D3/LL ≈ 2.0 just before a new B-layer occurring in the channel. At D3/LL ≈ 3.0, there is another peak when the system will create a third B-rich layer. From this observation, we can deduce that the structural frustration in the form of chain stretching is released through forming a new B-rich layer in the system. Before each peak, increases with the increase of D3/LL in regions of D3/LL ≈ 1.0 ∼ 2.0 and 2.6 ∼ 3.0. After each peak, decreases with the increase of D3/LL in regions of D3/LL ≈ 2.0 ∼ 2.6 and 3.0 ∼ 3.6. The variation of reflects that the layer thickness is adjusted periodically with the increase of D3/LL. For a strongly selective surface with α = 1.0, the variation trend of is similar to that in the weakly selective surface case. For 1.5 < D3/LL < 2.4, chains in the triangular-prism-shaped B-cylinder are stretched more and more heavily with the increases of D3/LL. At D3/LL ≈ 2.6, the chain stretching is released by the morphological transition from a triangular-prism-shaped B-cylinder to tridentate B-lamella. Another chain stretching releasing is observed at D3/LL ≈ 3.9 where a new A-cylinder appears in the center of the channels. Whereas at D3/LL ≈ 3.7, the chain stretching is not released though a new ring of A-spheres appears in the center of the channels. This is because the morphologies at D3/LL ≈ 3.7 are closer to those at D3/LL ≈ 3.5 than those at D3/LL ≈ 3.9, so that we can define morphologies at D3/LL ≈ 3.9 as the transition to form a new layer. Although many morphological differences exist between the weakly and the strongly selective surface cases, one common feature is that the value in these two cases increases with increasing the channel size and the periodically morphological transitions are driven by releasing the structural frustrations in the form of chain stretching.

Figure  2(b) shows the variations of NAB with D3/LL for the same cases as those shown in Fig.  2(a). As a comparison, the bulk value of NAB is also plotted in the figure. As shown in Fig.  2(b), for neutral surfaces, the value of NAB is slightly smaller than the bulk value in smaller channels, and nearly equal to the bulk value in larger channels. Combining this information and that from the curve shown in Fig.  2(a), we can deduce that the existence of the boundary has little effect on the chain conformation in the case of the neutral surface. For the weakly selective surface, the value of NAB is much smaller than that in the bulk. This observation indicates that the stacked parallel lamellae observed at intermediate α values are the interfacial energy favored structures compared with the perpendicular lamellae formed in the case of the neutral surface. On the other hand, the NAB curve with α = 0.2 is almost a reverse version of the corresponding curve. There are several minima in the NAB curve which correspond to the maxima in the curve. This observation is reasonable considering the fact that the occurrence of a new B-layer will surely increase the contact between A and B blocks. For the strongly preferential surface, the variation of NAB is quite different from those in the neutral and weakly selective cases. For this case, the overall variation trend of the NAB curve decreases with the increase of D3/LL. The slope of the NAB curve is sharp when D3/LL < 2.4 where the morphology inside the channel is a circular or a triangular-prism-shaped B-cylinder. In the region of D3/LL ≈ 2.6∼ 3.5 where the morphology is tridentate lamellae, the slope of the NAB curve decreases. When a new A-cylinder occurs in the center of the channel, NAB slightly increases but it is still smaller than the bulk value.

Fig.  2. Plots of (a) the mean-square end-to-end distance of chains and (b) the average contact number NAB versus D3/LL for three typical surfaces in channels with regular triangle-shaped cross sections. In panel (a), is plotted in units of the mean-square end-to-end distance of the corresponding ideal Gaussian chain.

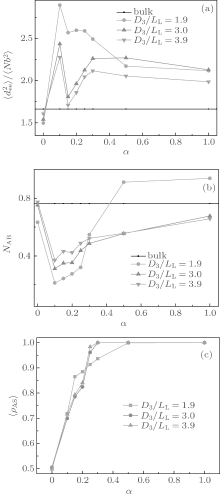
The effect of surface selectivity on the chain conformation is also investigated. Figures  3(a) and 3(b) show the variations of and NAB, respectively with α at three typical channel sizes (D3/LL ≈ 1.9, 3.0, 3.9). As shown in Fig.  3(a), all curves have a similar trend, and are larger than the bulk value for selective surfaces. In each curve, there is a peak at α = 0.1 and a minimum at α = 0.15 follows. When α > 0.15, the variation of a curve depends on D3/LL. For a small channel such as at D3/LL ≈ 1.9, decreases in the region of α = 0.15 ∼ 0.5, and the value of at α = 0.5 is very close to that at α = 1. For larger channels with D3/LL > 3.0, increases in the region of α = 0.15∼ 0.3 and the value of at α = 0.3 is very close to that at α = 1. The values of at α = 0 and α = 1 depend on D3/LL as shown in Fig.  2(a). Comparing Fig.  3(a) with Fig.  1, we notice that the peak of a curve corresponds to a frustrated structure and the followed minimum corresponds to a stacked parallel lamellar structure.

In Fig.  3(b), we see that all NAB curves vary in a similar way. The NAB value is very close to the bulk value for a neutral surface. Each NAB curve has a minimum at α = 0.15 where the corresponding curve presents a peak, then almost keeps the minimum value in the range of 0.15 ≤ α ≤ 0.3, and at α > 0.3 arrives at a value that is close to the value at α = 1. From Figs.  3(a) and 3(b), it is deduced that the interfacial energy is favorable for the formation of complex morphologies in the range of 0.15 ≤ α ≤ 0.3, and this favorable interfacial energy has compensated for the entropic loss due to the chain stretching in these morphologies.

Fig.  3. Plots of (a) the mean-square end-to-end distance of chains and (b) the average contact number NAB, and (c) the surface concentration of A-monomer ρ AS versus α in channels with regular triangle-shaped cross sections.

The surface concentration of A-monomers is defined as ρ AS = NAS/(NAS + NBS), where NAS (NBS) is the average contact number between each A-(B-)monomer and the surface sites. ρ AS as a function of α is related to the surface energy and is plotted in Fig.  3(c). From Fig.  3(c) it follows that ρ AS = 0.5 at α = 0, which is consistent with the fact that the neutral surface gives no preference to the two blocks. Each ρ AS curve increases with α , and reaches a maximum value of 1 at α = 0.5 for the curve with D3/LL ≈ 1.9 and also at α = 0.3 for the curve with D3/LL ≥ 3.0. When ρ AS reaches 1 there is no contact between B-monomers and the surface, indicating that the surface selectivity is strong enough. When comparing Fig.  3(c) with Figs.  3(a) and 3(b) separately, it is noticed that the values of and NAB almost keep constant when ρ AS = 1. However, it is also noticed that the α value at which ρ AS reaches 1 is larger for a small channel with D3/LL ≈ 1.9 than that for larger channels with D3/LL > 3.0. This observation indicates that the surface energy is dominant for even weakly selective surfaces at larger D3/LL.

The formation mechanism of the morphologies shown in Fig.  1 could be discussed by analyzing the chain stretching, the interfacial and surface energies in terms of , NAB, and ρ AS, respectively. In principle, the observed morphology is a result of the competition among the stretching energy, interfacial energy and surface energy. In the neutral surface case, the surface gives no preference to the two blocks so that the A- and B-monomers divide the surface equally, which results in ρ AS = 0.5 as shown in Fig.  3(c). In this case, the surface energy equals zero and the copolymers prefer to form the bulk morphology in which the stretching energy and interfacial energy are peer-to-peer. As a result, stacked perpendicular lamellae are obtained. In the strongly selective surface case, the surface energy becomes a dominating factor affecting the ultimate self-assembled morphology. The surface is covered by the surface-preferred A-monomers, and the tridentate lamellae become the optimal structures inside the outermost A-layer. In the weakly selective surface case, the competition between the stretching energy and surface energy makes the interfacial energy turn into a dominating factor. As a result, multiple frustrated morphologies with a lower interfacial energy but a larger entropic loss due to the chain stretching are formed at α = 0.1. When the selectivity reaches α = 0.15∼ 0.2, stacked parallel lamellae, with lower interfacial and stretching energies as shown in Figs.  3(a) and 3(b), are obtained. This observation illustrates that the stacked parallel lamellae are the optimized equilibrium morphologies in these parameter spaces. From the above discussion, we can see that the polymer– wall interaction is very important and the value of α determines the ultimate self-assembled morphology. The addition of surface energy due to the confinement changes the competition between the stretching energy and interfacial energy compared with the case of the bulk system. Different self-assembled morphologies are spontaneously formed with the variation of α as a result of competition among the stretching energy, interfacial energy, and surface energy. The effect of single-wall carbon nanotube on the configuration of the insertion materials has been studied by Jiang et al., [47] and Li and Chen.[48] They found that the Van der Waals interaction plays an important role in these systems.

3.2. Channels with square-shaped cross section

In this case, typical self-assembled morphologies formed with the variations of D4/LL and α are shown in Fig.  4. In the neutral surface case of α = 0, perpendicular lamellae are observed regardless of D4/LL, where each lamella presents to be of a square shape, and the period of lamellae in a perpendicular lamellar structure has the value LL. For a strongly selective surface with α = 1, concentric lamellae occur in which the number of A– B interfaces increases with D4/LL. These observations are similar to those obtained in cylindrical channels, [29] but a detailed comparison reveals many differences. For the concentric lamellae, the shape of the outermost interface between the wetting A-layer and the channel-surface is always a square in the cross section, which is the shape of the channel. However, the shape of the inner interface of the wetting A-layer, i.e. the outermost A– B interface, depends on D4/LL. For small channels with D4/LL < 2.4, the shape of the outermost A– B interface is a circle in the cross section whereas for larger channels it is a square. On the other hand, except the outermost A– B interface, the shape of the inner A– B interface is still a circle regardless of D4/LL. This observation indicates that the confinement effect is stronger near the boundary and weaker in the center of the channel. It is also noticed that the center of the channel is alternatively occupied by an A-cylinder or a B-cylinder with the increase of the A– B interface number. As shown in Fig.  4, the transition of the alternatively occupying always occurs when the channel size is slightly smaller than an integral multiple of the bulk period (D4/LL ≈ 1.8, 2.8), which is different from that in the cylindrical channel case where the transition points occur when D/LL is slightly larger than an integer, where D is the diameter of the cylindrical channel. The reason could be attributed to the fact that the volume of a square-shaped channel is larger than that of a cylindrical channel with D = D4.

For the weakly selective surface, a rich variety of complex morphologies are obtained. At α = 0.1, the self-assembled morphologies depend on D4/LL. Stacked lamellae parallel to one pair of the channel side surfaces (type-I parallel lamellae) are observed when D4/LL is close to an integer (D4/LL ≈ 1.0∼ 1.2, 1.9∼ 2.1, 2.9∼ 3.0). For several type-I parallel lamellar structures, we compute the order parameter profile along the direction perpendicular to the lamellae, denoted as the x direction, to provide detailed information about the morphology. The order parameter is defined as Ψ (x) = 〈 φ B(x)〉 / 〈 φ A(x) + φ B(x)〉 , where φ i(x) (i = A or B) denotes the ratio of the number of the i-monomers to the number of lattice sites in a layer at a distance x to one side surface of the channel, and 〈 〉 denotes the ensemble average over all the collected configurations after equilibrium.[30] As shown in Fig.  5, Ψ (x) oscillates between 0 and 1 and the shape of Ψ (x) is square-wavelike, indicating that our simulations are in the strong segregation regime. It is noticed that the thickness of an A- or B-rich layer is roughly equal to LL/2 for an inner layer, and equal to LL/4 for the A-rich layer close to the surface, insensitive to D4/LL. This is consistent with the results shown in Fig.  4 where type-I parallel lamellae are observed only when the channel size is commensurate with the bulk period LL. When the channel size is incommensurable with LL, tilted lamellae, defective single helices (S-helices) and S-helices are observed in small (D4/LL ≈ 1.3∼ 1.7), intermediate (D4/LL ≈ 1.8, 2.2∼ 2.7), and large (D4/LL ≈ 2.8, 3.1∼ 3.2) channels, respectively. It is also noticed that the period of the tilted lamellae and the pitch of the S-helices or defective S-helices are both much larger than LL.

Fig.  4. Self-assembled morphologies formed with the variations of D4/LL and α for symmetric diblock copolymers confined in channels with square-shaped cross sections. For clarity, the structure of domain B is also shown separately for some special morphologies. For some concentric lamellar structure, a cross section view is also given. When the same type of morphology is formed at a given D4/LL but in a range of α values, only these morphologies at the two boundary α values are shown.

It is interesting to notice that type-I parallel lamellar structures can also be obtained at α = 0.2, and even when D4/LL is very far from an integer, such as at D4/LL ≈ 2.4, and 2.7. Furthermore, stacked lamellae parallel to the diagonal of the square (type-II parallel lamellae) are obtained at D4/LL ≈ 1.8 and 2.8 with α = 0.15∼ 0.2. Parallel lamellae imbedded into the channel with a complete wetting A-layer, are observed in a wide range of D4/LL at α = 0.2∼ 0.35, as shown in Fig.  4. These parallel lamellae structures are quite different from those observed in the case of cylindrical channels.[29] In general, the numbers of A– B interfaces in type-I, type-II, and imbedded parallel lamellae all increase with D4/LL. On the other hand, it is noticed that the distances between two neighboring lamellae in these structures are all much larger than LL for channels with relatively stronger selectivity of α = 0.3 at D4/LL ≈ 3.0 ∼ 3.1. In addition to the stacked parallel lamellae, a series of folding lamellae are obtained in large channels. As shown in Fig.  4, U-shaped and UI-shaped lamellae occur at D4/LL ≈ 2.7∼ 2.9 and D4/LL ≈ 3.0∼ 3.1, respectively, in the range of α = 0.2 ∼ 0.25. S-shaped lamellae are observed at D4/LL ≈ 3.0 with α = 0.25 ∼ 0.3 and at D4/LL ≈ 3.2 with α = 0.3 ∼ 0.35. OI-shaped lamellae are observed at D4/LL ≈ 3.0∼ 3.1 with α = 0.25 and D4/LL ≈ 3.2 with α = 0.35. Especially, lamellae with an AB-layer at the surface are obtained at D4/LL ≈ 3.2 with α = 0.4. U-shaped lamellae are obtained in the previous study when the same diblock copolymers confined in cylindrical channels.[29] Except U-shaped lamellae, the above-mentioned other types of folding lamellae have never been observed or predicted for the same copolymers confined in a cylindrical channel.

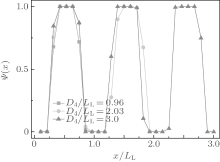Fig.  5. Variations of order parameter Ψ (x) for stacked parallel lamellae with x/LL at α = 0.1 for different D4/LL values.

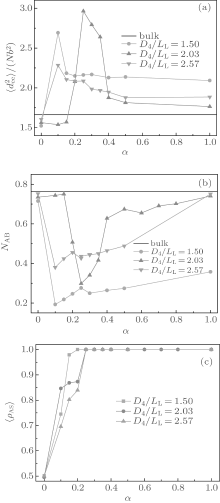
The curves of mean-square end-to-end distance and the average contact number NAB versus D4/LL for three typical surfaces and the corresponding bulk value are plotted in Fig.  6. In Fig.  6(a), it is noticed that for neutral surfaces with α = 0, chains are always slightly compressed with respect to the bulk chains, which is similar to the cases when the same copolymers are confined in channels with regular triangle-shaped cross sections studied in the previous section and in cylindrical channels.[29] For weakly (α = 0.1) and strongly (α = 1) selective surfaces, the variations of are similar to each other, where each curve oscillates with D4/LL. For the strongly selective surface case, the curve presents two peaks at the positions when the channel size is about a half integral multiple of LL(D4/LL ≈ 1.5, 2.5), and two minima at the positions when the channel size is about an integral multiple of LL(D4/LL ≈ 2.0, 3.0). The peaks of correspond to conformations where the chains are in a strongly stretched state, that is, the most frustrated case. On the other hand, the minima of are close to the bulk value, indicating that the conformations of chains are close to that in the bulk. By comparison with Fig.  4, it is interesting to notice that the decrease of from a peak to a minimum corresponds to a transition from a concentric lamellar structure with a central domain of one block to that with a central domain of the other block. This observation demonstrates that the alternation of the center blocks is driven by the release of structural frustrations due to the chain stretching. For the weakly selective surface case, the value of is much larger than the bulk value when the channel size deviates from an integral multiple of LL. However, when D4/LL is close to an integer, is slightly smaller than the bulk value. Comparing Fig.  6(a) with Fig.  4, we notice that the morphologies with larger correspond to S-helices or complex structures with larger periods. The minima of correspond to the type-I parallel lamellae in which the sizes of one A-rich-layer and one B-rich-layer are close to the bulk period LL as shown in Fig.  5.

From Fig.  6(b), it is noticed that each NAB curve is almost an inverse version of the corresponding curve shown in Fig.  6(a). As mentioned above, the existence of the boundary has little effect on the chain conformation for the neutral surface case. Therefore, it is reasonable that when α = 0 NAB is very close to the bulk value. Furthermore, it is also noticed that in the cases of weakly and strongly selective surfaces, the values of NAB are also close to the bulk value at D4/LL ≈ 2.0 and 3.0, while they are much smaller than the bulk value when D4/LL deviates from an integer. Therefore, it is the interfacial energy, represented by the contact number between A- and B-monomers, that is favorable for the formation of complex morphologies.

Figure  7 shows the variations of , NAB and ρ AS with α at three typical channel sizes (D4/LL ≈ 1.5, 2, 2.6). As shown in Fig.  7(a), all the curves have a similar trend. That is, the value is slightly smaller than the bulk value at α = 0, each curve presents a peak at a small α value where the chains are strongly stretched, and after the peak, the value of is close to that at α = 1. This trend is different from that in the case when the same copolymers are confined in channels with triangle-shaped cross sections but similar to that in the case when the same copolymers are confined in cylindrical channels.[29] The NAB curves shown in Fig.  7(b) demonstrate that the average contact number between A- and B-monomers is close to that in the bulk phase for the neutral surface case. Each NAB curve has a minimum at the α value where the corresponding curve (shown in Fig.  7(a)) presents a peak, after the minimum, NAB slightly increases with the increase of α . From Fig.  7(c), it is noticed that with the increase of α , each ρ AS curve increases rapidly from 0.5 at α = 0 to 1 at α ≈ 0.2.

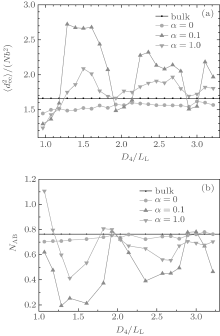Fig.  6. Plots of (a) the mean-square end-to-end distance of chains and (b) the average contact number NAB versus D4/LL in the case of channels with square-shaped cross sections.

Like the result for the triangle-shaped channels, the formation of the morphologies shown in Fig.  4 is also due to the competition among the stretching energy, interfacial energy and surface energy. In the neutral surface case, the surface energy equals zero and stacked perpendicular lamellae are the optimal morphologies. In the strongly selective surface case, concentric lamellae with a lower surface energy are the signature morphology. In the weakly selective surface case, the interfacial energy becomes an important factor and multiple frustrated morphologies are formed. However, it is noticed that the frustrated structures obtained in this case are much more abundant than those obtained in the case of triangle-shaped channels. The reason may be attributed to the difference in confinement geometry. For square-shaped channels, the confinement space is larger than that for the triangle-shaped channels when D3= D4. Therefore, much more freedom is provided in a square-shaped channel and the entropic loss of the frustrated morphologies may be less than that confined in a triangle-shaped channel. This observation implies that all of the stretching energy, interfacial energy and surface energy can strongly affect the resulting morphologies within a square-shaped channel.

Fig.  7. Plots of (a) the mean-square end-to-end distance of chains , (b) the average contact number NAB, and (c) the surface concentration of A-monomer ρ AS versus α in the case of square-shaped cross sections.

3.3. Channels with ellipse-shaped cross sections

For channels with ellipse-shaped cross sections, typical morphologies as a function of Dey/LL are presented in Fig.  8. In Figs.  8(a)– (c), 8(d), and 8(e), we fix Dex/LL ≈ 2, Dex/LL ≈ 1.5, and Dex/Dey ≈ 1.5, respectively, while change Dey/LL in steps of about 0.2. In Fig.  8(a), it is noticed that stacked perpendicular lamellae are the unique structures obtained for neutral surfaces with α = 0. For the strongly selective surface with α = 1, concentric lamellae always occur as shown in Fig.  8(b), in which the number of A– B interfaces seems to be dependent only on the size of the minor axis. For the weakly selective surfaces with α = 0.1 and Dex/LL ≈ 2 as shown in Fig.  8(c), it is noticed that when Dey/LL ≤ 2.1, the majority morphologies are the stacked perpendicular lamellae except that at Dey/LL ≈ 1.2 ∼ 1.3 where a B-twisted parallel lamellar structure is formed. The period of stacked perpendicular lamellae equals LL at Dey/LL ≈ 1.5 ∼ 1.9, and it is much larger than LL at Dey/LL ≈ 2.1. In the B-twisted parallel lamellar structure, the surface-preferred A-blocks form two thin layers along the channel and near the wall, while the B-blocks form a twisted lamella sandwiched between the two A-layers. When Dey is larger than Dex (Dey/LL ≥ 2.2), a series of stacked parallel lamellae along the channel with flat or curved A– B interfaces, called type-III parallel lamellae, is observed. Although the orientations of the stacked parallel lamellae are not uniform, one common feature as shown in Fig.  8(c) is that the number of B-layers in a stacked parallel lamellar structure keeps a value of 2, which is consistent with the value of Dex/LL. In Fig.  8(d), it is interesting to notice that stacked parallel lamellae are obtained only at Dey/LL ≈ 1.3 and followed by a B-twisted structure and a parallel lamellar structure at Dey/LL ≈ 1.5, while for the other values of Dey/LL, stacked perpendicular lamellae and/or undulated perpendicular lamellae (Dey/LL ≈ 2.1, 4.1) are obtained. Stacked parallel lamellae are not observed for larger channels in Fig.  8(d) even when the length of the major axis is commensurate with the bulk period LL (Dey/LL ≈ 2.0, 3.0, 4.0). These results imply that the morphologies of stacked parallel lamellae occur only when the length of the minor axis of the ellipse-shaped cross section is commensurate with the bulk period LL. To verify this assumption, simulations with a fixed ratio of Dex/Dey ≈ 1.5 while increasing the two lengths simultaneously are performed, and the typical morphologies are presented in Fig.  8(e). It is interesting to notice that stacked parallel lamellae along the channel are observed only when the length of the minor axis is nearly commensurate with the bulk period at Dey/LL ≈ 1.1, 1.9 ∼ 2.1, and 3.0. It is also noticed that the number of B-layers in a stacked parallel lamellar structure increases with Dey/LL. On the other hand, twisted lamellae (at Dey/LL ≈ 1.3 and Dex/LL ≈ 2.0) and imperfect S helices (at Dey/LL ≈ 2.6 and Dex/LL ≈ 4.0) are observed when the length of the major axis is nearly commensurate with LL.

The formation mechanism of these morphologies could be discussed by analyzing the chain stretching, interfacial and surface energies. For the case of weakly selective surfaces with Dex/LL ≈ 2, corresponding to the morphologies shown in Fig.  8(c), the mean-square end-to-end distance and the average contact numbers of monomers as a function of Dey/LL are shown in Fig.  9. As shown in Fig.  9(a), for perpendicular lamellae with period LL, is slightly smaller than the bulk value, indicating that the chains are always slightly compressed with respect to the unconfined chains. On the other hand, for other morphologies shown in Fig.  8(c), is much larger than the bulk value, revealing that the chains are strongly stretched. This observation indicates that the perpendicular lamellae with a period LL is entropy favored with less stretching energy whereas the other morphologies endure a high stretching energy. It is also noticed that the value for a type-III parallel lamellar morphology increases with increasing the channel size in the range of Dey/LL ≈ 2.2 ∼ 3.9. The reason for this is that the number of B-layers keeps as a constant of 2 within this region, and hence the chains are increasingly stretched with the increase of Dey/LL. When Dey/LL increases to 3.9, two degenerated type-III parallel lamellar morphologies are observed and only one of them keeps the only observed morphology at Dey/LL ≈ 4.1. As shown in Fig.  9(a), the values for the two degenerated morphologies at Dey/LL ≈ 3.9 are quite different, and the same behavior occurs at Dey/LL ≈ 4.3. From this observation, we can conclude that the morphological transition between two type-III parallel lamellar morphologies with different orientations is driven by releasing the structural frustration from the chain stretching, and the two degenerated morphologies at Dey/LL ≈ 3.9 are the coexistent state of structures before and after the transition.

Fig.  8. Self-assembled morphologies of symmetric diblock copolymers confined in channels with ellipse-shaped cross sections as a function of Dey/LL with (a) Dex/LL ≈ 2, α = 0; (b) Dex/LL ≈ 2, α = 1; (c) Dex/LL ≈ 2, α = 0.1; (d) Dex/LL ≈ 1.5, α = 0.1; and (e) Dex/Dey ≈ 1.5, α = 0.1.

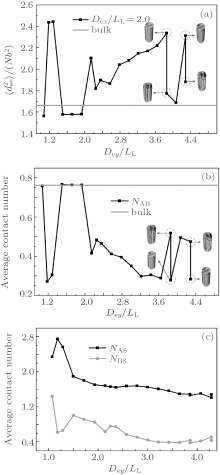The variation of the average contact number of an A-monomer with B-monomers, NAB, is plotted in Fig.  9(b). The NAB equals the bulk value for perpendicular lamellae with period LL, and it is much smaller than the bulk value for the other morphologies shown in Fig.  8(c). Comparing Fig.  9(b) with Fig.  9(a), it is interesting to notice that the NAB curve is almost an inverse of the curve. The more stretching of chains in a morphology, the smaller NAB is obtained. This observation illustrates that morphologies with high stretching energies are enthalpy favored.

Fig.  9. Dependences of (a) the mean-square end-to-end distance , (b) the average contact numbers NAB, and (c) NAS and NBS, on Dey/LL with Dex/LL ≈ 2 and α = 0.1.

The variation of the average contact number of an A-(or  B-)monomer, NAS (NBS) with the channel surface is shown in Fig.  9(c). It is noticed that NAS is always larger than NBS due to the A-selectivity of the surface. The variation tendencies of both NAS and NBS curves are similar to each other. In general, NAS and NBS decrease with increasing the channel size except at Dey/LL ≈ 1.2 ∼ 1.3 where the NAS curve presents a peak while the NBS curve presents a minimum, indicating that the B-twisted lamellae formed at Dey/LL ≈ 1.2 ∼ 1.3 is favored by the surface energy. It is also noticed that there are only small differences in both NAS and NBS between the two degenerated morphologies at Dey/LL ≈ 3.9 and 4.3.

In summary, the formation of an observable morphology is a competition among the stretching energy, interfacial energy, and surface energy. In a small channel, the stretching energy is the dominating factor. Perpendicular lamellae are the optimal morphology when the length of the minor axis of the channel is incommensurate with the bulk period. However, when Dey/LL is slightly larger than an integer, complex morphologies such as B-twisted lamellae and perpendicular lamellae with longer periods could form with favorable interfacial and surface energies to compensate for the entropic loss due to the chain stretching. In a larger channel, the confinement effect is weakened and the stretching energy becomes less important. Therefore, the interfacial energy becomes the dominating factor. When the length of the minor axis is commensurate with LL, type-III parallel lamellae are favorable since they have a lower interfacial energy compared with the perpendicular lamellae. The reason why the stacked parallel lamellae along the major axis have not been observed even when the length of the major axis is commensurate with LL may be attributed to the higher interfacial energy coming from the larger A– B interfaces. On the other hand, when the length of the minor axis equals a half integral multiple of LL, which corresponds to an extremely frustrated case, perpendicular lamellae with their lower stretching energy are expected to be the optimized structure. In fact, for the case with Dex/LL ≈ 1.5, perpendicular lamellae are observed when Dex < Dey as shown in Fig.  8(d). The and NAB curves corresponding to morphologies in Fig.  8(d) are plotted in Fig.  10. As shown in Fig.  10, the and NAB values for the perpendicular lamellae are similar to those shown in Fig.  9. However, when the length of the major axis of the channel is nearly commensurate with LL(Dey/LL ≈ 2.1, 4.1), undulated perpendicular lamellae are also observed as a degenerated morphology with the perpendicular lamellae. From Fig.  10, it is noticed that for the undulated perpendicular lamellae, their values are much larger than the bulk value, whereas their NAB values are much smaller than the bulk value. This observation indicates that at those channel sizes, the entropic effect is weakened and the interfacial energy is dominating. For the case with a fixed Dex/Dey ≈ 1.5, corresponding to morphologies in Fig.  8(e), the variations of and NAB with Dey/LL are shown in Fig.  11. It is noticed that like the cases with Dex/LL ≈ 1.5 and 2.0, perpendicular lamellae have favorable stretching energy having a small value. The other observed morphologies in Fig.  8(e), including perpendicular lamellae with larger LL, stacked parallel lamellae and S helices, own a favorable interfacial energy to compensate for the entropic loss in the form of chain stretching.

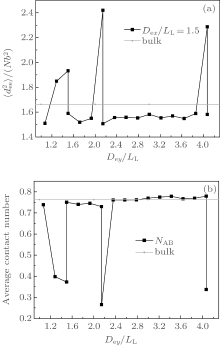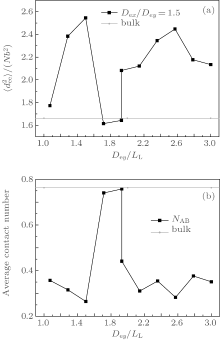Fig.  10. Dependences of (a) the mean-square end-to-end distance and (b) the average contact numbers NAB on Dey/LL with Dex/LL ≈ 1.5 and α = 0.1.

Fig.  11. Plots of (a) the mean-square end-to-end distance and (b) the average contact numbers NAB versus Dey/LL with Dex/Dey ≈ 1.5 and α = 0.1.

4. Comparison with results of cylindrical channels

The self-assembly of lamella-forming diblock copolymers confined in nanochannels with circular cross sections, i.e., cylindrical channels, has been extensively studied by experiments, [18– 21, 23, 24] theoretical calculation, and simulations.[25, 26, 29, 30, 32– 35, 37] A multiple set of concentric lamellae with the PBD block located at the wall of the channels was observed in experiment for symmetric PS-b-PBD diblock copolymers confined in a cylindrical channel of alumina membranes with a selective channel-wall.[18] Furthermore, it was noticed that the center of the channels could be PBD or PS domains depending on the diameter of channels.[20] Concentric lamellae were observed in theoretical and simulation studies for symmetric diblock copolymers confined in cylindrical channels with a strongly selective channel-wall, which is in agreement with the experimental results.[25, 26, 29, 30, 32– 35, 37] For channels with neutral surfaces, lamellae normal to the channel axis (perpendicular lamellae) were predicted in simulations.[26, 29, 30, 33, 34, 36] For channels with weakly preferential surfaces for one of the blocks, novel morphologies, such as porous lamellar (mesh) morphologies, stacked parallel lamellae as well as helices or mixed morphologies were predicted with simulations.[28, 29, 32, 33, 35]

For channels with regular triangle-shaped cross sections, the self-assembled morphologies are quite different from those observed in cylindrical channels. First, concentric lamellar structures have not been observed in this case for the studied channel sizes. Instead of concentric lamellae, triangular-prism-shaped cylinders along the channel axis and tridentate lamellae are obtained for strongly selective surfaces. This observation indicates that the block copolymers are to remain in their bulk structures in channels of low-symmetric cross sections. The second difference is that the stacked parallel lamellae are obtained for all channel sizes studied in the case of weakly selective surfaces. The previous simulations[29, 34] of symmetric diblock copolymers confined in cylindrical channels showed that the stacked parallel lamellar structures occur only when the channel size is nearly commensurate with the bulk period and with the surface selective parameter α ≈ 0.1.[29] In that case, slight deviation of the α value from 0.1 will result in the morphological transitions from stacked parallel lamellae to perpendicular lamellae or to concentric lamellae. Furthermore, slight deviation of the channel size from the commensurability with the bulk period will result in morphological transitions from stacked parallel lamellae to helices or mixed morphologies.[29] In channels with regular triangle-shaped cross sections, stacked parallel lamellae are observed at a wider parameter space of α ≈ 0.15 ∼ 0.2 regardless of the size of the channels. However, morphologies such as porous lamellar as well as helices, observed in cylindrical channels, have never been observed in triangle-shaped channels. On the other hand, some common features are observed between the two types of confinement boundaries. The stacked perpendicular lamellae are observed in both cases for neutral surfaces. For the strongly selective surfaces, the surface preferred monomers form a wetting layer over the channel-wall and the center domain could be occupied by either A- or B-block depending on the size of the channels. These results reflect that the basic principle is the same in all cases, and the low-symmetry of triangle-shaped cross sections prevents the system from forming concentric lamellae and helices.

For channels with square-shaped cross sections, the self-assembled morphologies are similar to those obtained in cylindrical channels. Perpendicular and concentric lamellae are obtained for neutral and strongly selective surfaces, respectively. The novel structures including stacked parallel lamellae, helices and U-shaped folding lamellae are obtained for weakly selective surfaces. However, there are differences between these two systems. For the strongly selective surfaces, it is interesting to notice that the outermost wetting A-layer is a square-shaped shell, and the outermost B-layer (green shell) is a shell with different shapes of outer and inner interfaces as shown in Fig.  4 when D4/LL > 2.4. The outer interface of the outermost B-layer is in a square shape, while the inner, in a circle shape. This observation demonstrates that the effect of the boundary shape may transfer to the outermost B-layer from the outermost A-layer. For the weakly selective surfaces, the stacked parallel lamellae are observed in a wider parameter space of D/LL and α in Fig.  4 compared with the case in cylindrical channels, which could be attributed to the directed effect of the boundary. Type-II parallel lamellae are obtained due to the additional orientation freedom in square-shaped channels. In addition, the multiple folding lamellae, such as U-shaped, UI-shaped, OI-shaped, imbedded, lamellae with an AB-layer at the surface, and type-II lamellae, observed in Fig.  4, have never been observed in previous studies for the same copolymer under cylindrical channel confinement. This result implies that the orientation of lamellae can be manipulated by fabricating differently shaped channels.

Unlike the cylindrical channel, the channel with an ellipse-shaped cross section has two characteristic lengths, which also makes the opportunity to control the lamellar orientation by tuning the sizes of Dx and Dy. From our present work, it is found that the stacked parallel lamellae always occur when the length of the minor axis is commensurate with the bulk period in the case of weakly selective surfaces.

5. Conclusions

In the present work, we systematically studied the self-assembly of lamella-forming symmetric diblock copolymers confined in nanochannels of various shaped cross sections using a simulated annealing method. The cross sections of the confining channels are of different shapes including regular triangles, squares, and ellipses. The results reveal that the geometry and surface property of the confining channels have a large effect on the self-assembled structure and the orientation of the lamellar structure. Stacked perpendicular lamellae with period LL are observed for neutral surfaces regardless of the channel shape and size, but each lamella is in a shape of the corresponding channel's cross section. For selective surfaces, the resulting morphologies depend on the shape, size, and selective strength of the channel.

For the channels with regular triangle-shaped cross sections, the stacked parallel lamellae are always observed when the surface selectivity is weak (α ≈ 0.15 ∼ 0.2) regardless of the sizes of channels. When the surface selectivity is strong enough, morphologies with a triangular-prism-shaped B-cylinder are obtained in small channels and tridentate lamellae are obtained in larger channels. These morphologies have never been observed or predicted previously. For the channels with square-shaped cross sections, the concentric lamellae are observed and the outermost AB interface can be in a square shape for strongly selective surfaces. For the weakly selective surfaces, novel morphologies such as stacked parallel lamellae, S-shaped, U-shaped, UI-shaped, OI-shaped, imbedded, and lamellae with an AB-layer at the surface are obtained. Specially, it is noticed that stacked parallel lamellae are observed in a wider parameter range of D/LL and α than those in the cylindrical channel case. For the channels with ellipse-shaped cross sections, the concentric lamellae are the unique morphology for strongly selective surfaces. For the weakly selective surfaces, the stacked parallel lamellae are the majority morphologies when the length of the minor axis is commensurate with the bulk period, whereas when the length of the minor axis is incommensurate with the bulk lamellar period, the stacked perpendicular lamellae are usually obtained.

The chain conformations including the mean-square end-to-end distance of chains , the average contact numbers between different species and the surface concentration of A-monomers are computed to elucidate the mechanisms of the formation of the different morphologies. It is found that the resulting morphology is a competition among the chain stretching, interfacial energy and surface energy. Our study provides a useful tool to produce new morphologies and to manipulate the orientation of lamellae in 2D confinement.

Reference
1 Cheolmin P, Yoon. J and Thomas E L 2003 Polymer 44 6725 DOI:10.1016/j.polymer.2003.08.011 [Cited within:1] [JCR: 3.379]
2 Park M, Harrison C, Chaikin P M, Register R A and Adamson D H 1997 Science 276 1401 DOI:10.1126/science.276.5317.1401 [Cited within:1]
3 Shin K, Leach K A, Goldbach J T, Kim D H, Jho J Y, Tuominen M, Hawker C J and Russell T P 2002 Nano Lett. 2 933 DOI:10.1021/nl0256560 [Cited within:1] [JCR: 13.025]
4 Urbas A M, Thomas E L, Kriegs H, Fytas G, Penciu R S and Economou L N 2003 Phys. Rev. Lett. 90 108302 DOI:10.1103/PhysRevLett.90.108302 [Cited within:1] [JCR: 7.943]
5 Khand pur A K, Forster S, Bates F S, Hamley I W, Ryan A J, Bras W, Almdal K and Mortensen K 1995 Macromolecules 28 8796 DOI:10.1021/ma00130a012 [Cited within:1] [JCR: 5.521]
6 Matsen M W and Bates F S 1996 Macromolecules 29 1091 DOI:10.1021/ma951138i [Cited within:1] [JCR: 5.521]
7 Laradji M, Shi A C, Nooland i J and Desai R C 1997 Macromolecules 30 3242 DOI:10.1021/ma9618437 [Cited within:1] [JCR: 5.521]
8 Matsen M W 1997 J. Chem. Phys. 106 7781 DOI:10.1063/1.473778 [Cited within:1] [JCR: 1.578]
9 Huang E, Russell T P, Harrison C, Chaikin P M, Register R A, Hawker C J and Mays J 1998 Macromolecules 31 7641 DOI:10.1021/ma980705+ [Cited within:1] [JCR: 5.521]
10 Wang Q, Yan Q L, Nealey P F and de Pablo J J 2000 J. Chem. Phys. 112 450 DOI:10.1063/1.480639 [Cited within:1] [JCR: 1.578]
11 Binder K and Muller M 2000 Curr. Opin. Colloid Interface Sci. 5 315 [Cited within:1] [JCR: 6.629]
12 Fasolka M J and Mayes A M 2001 Ann. Rev. Mater. Sci. 31 323 DOI:10.1146/annurev.matsci.31.1.323 [Cited within:1]
13 Park C, Yoon J and Thomas E L 2003 Polymer 44 6725 DOI:10.1016/j.polymer.2003.08.011 [Cited within:1] [JCR: 3.379]
14 Yin Y H, Sun P C, Chen T H, Li B H, Jin Q H, Ding D T and Shi A C 2004 Chemphyschem 5 540 DOI:10.1002/(ISSN)1439-7641 [Cited within:2] [JCR: 3.349]
15 Lambooy P, Russell T P, Kellogg G J, Mayes A M, Gallagher P D and Satija S K 1994 Phys. Rev. Lett. 72 2899 DOI:10.1103/PhysRevLett.72.2899 [Cited within:2] [JCR: 7.943]
16 Pan J X, Zhang J J, Wang B F, Wu H S and Sun M N 2013 Chin. Phys. B 22 026401 DOI:10.1088/1674-1056/22/2/026401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
17 Xiang H Q, Shin K, Kim T, Moon S I, McCarthy T J and Russell T P 2005 Macromolecules 38 1055 DOI:10.1021/ma0476036 [Cited within:4] [JCR: 5.521]
18 Shin K, Xiang H Q, Moon S I, Kim T, McCarthy T J and Russell T P 2004 Science 306 76 DOI:10.1126/science.1100090 [Cited within:5]
19 Xiang H Q, Shin K, Kim T, Moon S I, McCarthy T J and Russell T P 2004 Macromolecules 37 5660 DOI:10.1021/ma049299m [Cited within:1]
20 Xiang H Q, Shin K, Kim T, Moon S I, McCarthy T J and Russell T P 2005 J. Polym. Sci. Part B: Polym. Phys. 43 3377 DOI:10.1002/(ISSN)1099-0488 [Cited within:3] [JCR: 2.221]
21 Dobriyal P, Xiang H Q, Kazuyuki M, Chen J T, Jinnai H and Russell T P 2009 Macromolecules 42 9082 DOI:10.1021/ma901730a [Cited within:3] [JCR: 5.521]
22 Sun Y, Steinhart M, Zschech D, Adhikari R, Michler G H and Gosele U 2005 Macromol. Rapid Commun. 26 369 DOI:10.1002/(ISSN)1521-3927 [Cited within:1] [JCR: 4.929]
23 Ma M L, Krikorian V, Yu J, Thomas E L and Rutledge G C 2006 Nano Lett. 6 2969 DOI:10.1021/nl062311z [Cited within:2] [JCR: 13.025]
24 Ma M L, Titievsky K, Thomas E L and Rutledge G C 2009 Nano Lett. 9 1678 DOI:10.1021/nl900265y [Cited within:2] [JCR: 13.025]
25 He X H, Song M, Liang H J and Pan C 2001 J. Chem. Phys. 114 10510 DOI:10.1063/1.1372189 [Cited within:5] [JCR: 1.578]
26 Sevink G J A, Zvelindovsky A V, Fraaije J and Huinink H P 2001 J. Chem. Phys. 115 8226 DOI:10.1063/1.1403437 [Cited within:6] [JCR: 1.578]
27 Yu B, Li B H, Jin Q H, Ding D T and Shi A C 2007 Macromolecules 40 9133 DOI:10.1021/ma071624t [Cited within:1] [JCR: 5.521]
28 Li W H, Wickham R A and Garbary R A 2006 Macromolecules 39 806 DOI:10.1021/ma052151y [Cited within:5] [JCR: 5.521]
29 Yu B, Sun P C, Chen T H, Jin Q H, Ding D T, Li B H and Shi A C 2007 J. Chem. Phys. 127 114906 DOI:10.1063/1.2768920 [Cited within:21]
30 Wang Q 2007 J. Chem. Phys. 126 024903 DOI:10.1063/1.2406078 [Cited within:6] [JCR: 1.578]
31 Li W H and Wickham R A 2006 Macromolecules 39 8492 DOI:10.1021/ma061630+ [Cited within:2] [JCR: 5.521]
32 Li W H and Wickham R A 2009 Macromolecules 42 7530 DOI:10.1021/ma900667w [Cited within:3]
33 Chen P, He X H and Liang H J 2006 J. Chem. Phys. 124 104906 DOI:10.1063/1.2178802 [Cited within:3] [JCR: 1.578]
34 Feng J and Ruckenstein E 2006 Macromolecules 39 4899 DOI:10.1021/ma0605954 [Cited within:5] [JCR: 5.521]
35 Feng J and Ruckenstein E 2006 J. Chem. Phys. 125 164911 DOI:10.1063/1.2362818 [Cited within:7] [JCR: 1.578]
36 Feng J, Liu H L and Hu Y 2006 Macromolecular Theory and Simulations 15 674 DOI:10.1002/(ISSN)1521-3919 [Cited within:3] [JCR: 1.606]
37 Li S B, Wang X H, Zhang L X, Liang H J and Chen P 2009 Polymer 50 5149 DOI:10.1016/j.polymer.2009.09.011 [Cited within:3] [JCR: 3.379]
38 Yu B, Sun P C, Chen T H, Jin Q H, Ding D T, Li B H and Shi A C 2006 Phys. Rev. Lett. 96 138306 DOI:10.1103/PhysRevLett.96.138306 [Cited within:3] [JCR: 7.943]
39 Yu B, Sun P C, Chen T H, Jin Q H, Ding D T, Li B H and Shi A C 2007 J. Chem. Phys. 126 204903 DOI:10.1063/1.2735626 [Cited within:2] [JCR: 1.578]
40 Chen P, Liang H J and Shi A C 2007 Macromolecules 40 7329 DOI:10.1021/ma0705164 [Cited within:1] [JCR: 5.521]
41 Wang Y, Qin Y, Berger A, Yau E, He C, Zhang L, Gosele U, Knez M and Steinhart M 2009 Adv. Mater. 21 2763 DOI:10.1002/adma.200900136 [Cited within:3] [JCR: 14.829]
42 Stewart-Sloan C R and Thomas E L 2011 Eur. Polymer J. 47 630 DOI:10.1016/j.eurpolymj.2010.10.013 [Cited within:1] [JCR: 2.562]
43 Shi A C, Li B H 2012 in Polymer Science: A Comprehensive Reference ed. Matyjaszewski K and Möller M Amsterdam Elsevier BV 7 71 81 [Cited within:1]
44 Shi A C and Li B H 2013 Soft Matter 9 1398 DOI:10.1039/c2sm27031e [Cited within:1] [JCR: 3.909]
45 Wang X H, Li S B, Zhang L X and Liang H J 2011 Chin. Phys. B 20 083601 DOI:10.1088/1674-1056/20/8/083601 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
46 Zhang L C, Sun M N, Pan J X, Wang B F, Zhang J J and Wu H S 2013 Chin. Phys. B 22 096401 DOI:10.1088/1674-1056/22/9/096401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
47 Jiang Y Y, Li H, Li Y F, Yu H Q, Liew K M, He Y Z and Liu X F 2011 ACS Nano 5 2126 DOI:10.1021/nn103317u [Cited within:3] [JCR: 12.062]
48 Li H and Chen W 2014 Sci. Rep. 4 3865 [Cited within:3] [JCR: 15.333]
49 Li Y F, Yu H Q, Li H, An C G, Zhang K, Liew K M and Liu X F 2011 J. Phys. Chem. C 115 6229 DOI:10.1021/jp1112262 [Cited within:1] [JCR: 4.814]
50 Cheng J, Zhang F, Chuang V P, Mayes A M and Ross C A 2006 Nano Lett. 6 2099 DOI:10.1021/nl061563x [Cited within:2] [JCR: 13.025]
51 Chuang V P, Cheng J, Savas T A and Ross C A 2006 Nano Lett. 6 2332 DOI:10.1021/nl061866r [Cited within:3] [JCR: 13.025]
52 Xu Y C, Xie N, Li W H, Qiu F and Shi A C 2012 J. Chem. Phys. 137 194905 DOI:10.1063/1.4765098 [Cited within:1] [JCR: 1.578]
53 Tan H G, Zhang M L, Deng Y J, Song Q G and Yan D D 2013 Polymer 54 6853 DOI:10.1016/j.polymer.2013.10.024 [Cited within:1] [JCR: 3.379]
54 Chen P, Liang H J, Xia R, Qian J S and Feng X S 2013 Macromolecules 46 922 DOI:10.1021/ma301203a [Cited within:1] [JCR: 5.521]
55 Zou Z X, He X H and Wang L 2012 J. Chem. Phys. 136 074902 DOI:10.1063/1.3685220 [Cited within:1] [JCR: 1.578]
56 Carmesin I and Kremer K 1998 Macromolecules 21 2819 [Cited within:1] [JCR: 5.521]
57 Larson R G 1989 J. Chem. Phys 91 2479 DOI:10.1063/1.457007 [Cited within:1] [JCR: 1.578]
58 Larson R G 1992 J. Chem. Phys. 96 7904 [Cited within:1] [JCR: 1.578]
59 Kirkpatrick S, Gelatt C D and Vecchi M P 1983 Science 220 671 DOI:10.1126/science.220.4598.671 [Cited within:1]
60 Kirkpatrick S 1984 J. Stat. Phys. 34 975 DOI:10.1007/BF01009452 [Cited within:1] [JCR: 1.4]
61 Grest G S, Soukoulis C M and Levin K 1986 Phys. Rev. Lett. 56 1148 DOI:10.1103/PhysRevLett.56.1148 [Cited within:1] [JCR: 7.943]
62 Chakrabarti A and Toral R 1989 Phys. Rev. B 39 542 DOI:10.1103/PhysRevB.39.542 [Cited within:1]