†Corresponding author. E-mail: lingcuicui@upc.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11374372), Natural Science Foundation of Shandong Province, China (Grant No. ZR2014EMQ006), the Postdoctoral Science Foundation of China (Grant No. 2014M551983), the Postdoctoral Applied Research Foundation of Qingdao City, China (Grant No. 2014), the Fundamental Research Funds for the Central Universities, China (Grant Nos. 12CX04087A and 14CX02018A), and the Qingdao Science and Technology Program, China (Grant No. 14-2-4-27-jch).
By employing molecular mechanics and molecular dynamics simulations, we investigate the radial collapses and elasticities of different chiral single-walled carbon nanotubes (SWCNTs) with divacancy, and 5-8-5 defects. It is found that divacancy and 5-8-5 defect can reduce the collapse pressure ( Pc) of SWCNT (10, 10) while 5-8-5 defect can greatly increase Pc of SWCNT (17, 0). For example, 5-8-5 defect can make Pc of SWCNT (17, 0) increase by 500%. A model is established to understand the effects of chirality, divacancy, and 5-8-5 defect on radial collapse of SWCNTs. The results are particularly of value for understanding the mechanical behavior of SWCNT with divacancy, and the 5-8-5 defect that may be considered as a filler of high loading composites.
Carbon nanotubes (CNTs) have been widely investigated due to their exceptional mechanical properties, such as high Young’ s moduli, excellent stiffnesses, and tensile strengths.[1– 5] Therefore, using CNTs as reinforcing fibers to enhance the mechanical properties of superstrong composite has also been studied extensively.[6– 8] In addition, it is found that the CNTs can provide mechanical stability for electric nano-circuits formed by CNTs with covalent inter-tube junctions.[9]
Recently, it has been demonstrated that there are always defects in CNTs, which are produced during CNT growth, purification, and the process of device or composite production.[10, 11] Moreover, people have found that the defects have a significant influence on the physical characteristics of CNTs.[12– 18] For example, defects are desired to increase adhesion between CNT and polymer matrix and further improve the mechanical characteristics of composite.[19, 20] Similarly, defects produced by electron irradiation may enhance the physical properties of bundles of CNTs.[21– 25] It has been found that a small dose irradiation can induce inter-tube links of CNTs, [26] and provide load transfer and enhance the shear modulus inside the CNTs bundle.[24] Nevertheless, a high-dose irradiation can induce many defects and accumulate the irradiation-induced defects and lead to the deterioration of mechanical characteristics of CNTs.
To date, the effect of defects on the mechanical properties of CNTs is not clear, which is very important for the design and application of CNT-based composites and devices. As is well known, molecular mechanics (MM) and molecular dynamics (MD) simulations can be employed for simulating the plastic behavior.[27– 32] In this paper, by employing MM and MD simulations, we study the effects of divacancy and 5-8-5 defects on the collapse pressure (Pc) of single-walled CNTs (SWCNTs). We also propose a method to estimate Pc of defective SWCNTs.
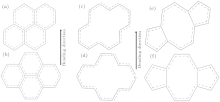
Since single vacancy and multi-vacancy defects are always presented in CNTs due to post-processing, including ion[33] and electron irradiation, [34] and so on. Moreover, these vacancies can transform into other defects by saturating the dangling bonds.[33– 36] It is demonstrated that vacancy defects have a great effect on the axial mechanical characteristics of individual SWCNTs.[24] Herein, we mainly concentrate on the responses of defective SWCNT (10, 10) and SWCNT (17, 0) to radial mechanical load. The one type of defect studied is a divacancy defect, as depicted in Figs. 1(c) and 1(d), which will be referred to as non-reconstructed defects.[24] The other type of defect studied is 5-8-5 defect, which is produced by saturating the dangling bonds with the adjacent carbon atoms. These configurations are presented in Fig. 1(e) for SWCNT (10, 10) and in Fig. 1(f) for SWCNT (17, 0). As is well known, the defect– defect interaction can influence the structural phase transition. Therefore, the lengths of all SWCNTs are set to be about 25 Å , thus the defect density (0.04 Å − 1) of SWCNT is low enough and this interaction does not significantly disturb the onset of radial collapse.
MD and MM simulations, which are implemented using a commercial software package called Materials Studio (MS) developed by Accelrys Software, Inc, are conducted to investigate the radial collapse of a series of SWCNTs with divacancy and 5-8-5 defects. In all of our MM and MD simulations, we have used COMPASS force-field, parametrized, tested and validated first ab initio force-field, which enables an accurate prediction of various gas-phase and condensed-phase properties of most of the common organic and inorganic materials.[37– 40] Moreover, it has been successfully used to study the mechanical properties and radial collapses of CNTs under hydrostatic pressure.[27– 32, 41, 42]
In the present paper, periodic boundary conditions are used in all systems, including intrinsic SWCNTs (10, 10) and (17, 0) and SWCNTs with divacancy and 5-8-5 defects with the same diameter and length of 25 Å . First, MM simulations are performed to find the thermal stable morphology and achieve a conformation with minimum potential energy for all SWCNTs. Second, MM simulations are carried out to optimize all SWCNT systems at atmospheric pressure, and the systems are subsequently subjected to step-wise monotonically hydrostatic pressure increments to investigate the radial collapses of all systems with FORCITE mode. After each pressure increment the unit cell volume is allowed to equilibrate for at least 30 ps at each step in the NPT ensemble, and a fixed time step size of 1 fs is used in all cases. An Andersen thermostat method is employed to control the system at a temperature of 1 K to avoid the thermal effect, and the interactions are determined within a cutoff distance of 9.5 Å . The reduced volume ratio (V/V0) gives information about the structural transition, which is obtained by measuring the unit cell volume after equilibration at each hydrostatic pressure.
CNTs can be seen as graphene crimped together along different angles, keeping the graphene sheet in the same hexagonal crimping process. So the chiral vector Ch = na1 + ma2 describes CNT, m and n are integers, a1 and a2 are the hexagonal lattice vector units. CNTs with different chiralities (n, m) have different atomic structures, when n = m, CNT is an armchair structure; when n = 0 or m = 0 CNT is zigzag structure; when the integers n and m are not the same, CNT is spiral-type structure. The initial atomic configuration of periodic SWCNT is obtained by creating the planar hexagonal carbon atom network corresponding to an SWCNT (n, m) cut open axially. The corresponding chiral angle θ and diameter Dn of an SWCNT with indices n and m could be determined using the rolling graphene model:[43]
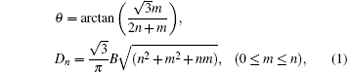
where B shows the C– C bond length, which is 1.42 Å . Here, we first investigate the radial collapse of the perfect SWCNT (10, 10) and SWCNT (17, 0). The intrinsic parameters of two chiral SWCNTs are shown in Table 1.
| Table 1. Values of atomic number, diameter, length, and angle parameters of different chiral SWCNTs. |
| Table 2. Energy differences between the collapsed SWCNTs and cylindrical SWCNTs with different chiralities. |
Figure 2 shows the loading and unloading curves of the intrinsic SWCNTs. It is shown that a hysteresis loop is observed in loading and unloading curves of SWCNT (10, 10), which indicates that the collapsed state of SWCNT (10, 10) is relatively stable. However, the loading and unloading curves of SWCNT (17, 0) cannot form a hysteresis loop, demonstrating that collapsed state of SWCNT (17, 0) is stable. Based on the above discussion, it is found that the SWCNT (10, 10) presents radial elasticity while SWCNT (17, 0) does not. Herein, the energy variation during the radial deformation of SWCNT is investigated to explain the radial elasticity of the chiral SWCNT. The internal and van der Waals (vdW) energy variations before and after collapse of SWCNTs are listed in Table 2. The different elasticity behaviors of two chiral SWCNTs can be understood by recognizing the role of the vdW interaction in stabilizing the collapsed geometry. After SWCNTs collapse, the opposite walls of SWCNTs have almost entered into the strong-adhesive-binding region of the chemical bonds and the attractive vdW force exists between the opposite walls of the collapsed SWCNTs.[27, 28, 30– 32] The attractive vdW force between the opposite walls makes the total vdW energy of SWCNTs decrease. For SWCNT (10, 10), the vdW energy variation is less than that of the internal energy, which shows that upon unloading the attractive vdW force is not large enough to stabilize the collapse state of SWCNT, and therefore SWCNT (10, 10) can return to the origin state. However, for SWCNT (17, 0) the vdW energy variation is more than that of the internal energy. In other words, upon unloading the attractive vdW force is large enough to stabilize the collapse state of SWCNT (17, 0). Therefore, SWCNT (17, 0) does not demonstrate radial elasticity.
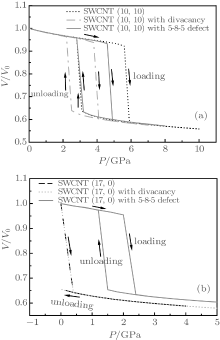 | Fig. 2. (a) Loading and unloading curves of (a) SWCNT (10, 10) and SWCNT (10, 10), and (b) SWCNT (17, 0) and SWCNT (17, 0), with divacancy and 5-8-5 defects. |
Herein, Pc is the pressure to collapse the SWCNT upon loading, which is used to describe its capacity of resistance to radial mechanical loading.[27] As shown in Table 3, it is found that Pc of SWCNT (10, 10) is much higher than that of SWCNT (17, 0), which indicates that SWCNT chirality has a great influence on the radial collapse of SWCNTs. In the next section, our theoretical model will be given and used to reveal the physical mechanism of the radial collapse of intrinsic SWCNTs.
| Table 3. Values of Pc and L of the corresponding SWCNT. |
As is well known, there is at least one defect in high-quality CNTs per 4 μ m.[44] Single vacancy and multi-vacancy are some of the most abundant and important point defects. It has been found that vacancy can deteriorate the deformation response of CNTs and further their mechanical characteristics and can also be underlying locations where an irreversible deformation response is started. However, defects formed by saturating dangling bonds of vacancies defects can give rise to many advantageous effects. For example, it may partly alleviate the deterioration in their mechanical characteristics and even enhance mechanical properties of SWCNT.[45]
In this section, we discuss the effects of divacancy and 5-8-5 defects on radial mechanical properties of SWCNT (10, 10) and SWCNT (17, 0). Figures 1(c)– 1(f) demonstrates the structures of SWCNT (10, 10) and SWCNT (17, 0) with divacancy and 5-8-5 defects, and their loading and unloading curves are shown in Fig. 2. It can be found that the divacancy and 5-8-5 defects have little influence on the radial elasticity of SWCNT (10, 10). All intrinsic SWCNT (10, 10), SWCNT (10, 10) with vacancy defect, SWCNT (10, 10) with 5-8-5 defect can return to their origin states. However, a 5-8-5 defect has a significant influence on the radial elasticity of SWCNT (17, 0), it make inelastic SWCNT (17, 0) change into elastic SWCNT (17, 0), which indicates that the 5-8-5 defect formed by saturating dangling bonds of divacancy defect can partly enhance the mechanical properties of SWCNT.
In order to further study the effects of divacancy and 5-8-5 defects on the radial collapse of SWCNT, we list the values of Pc of the SWCNTs in Table 3. It is found that the values of Pc of the intrinsic SWCNT (10, 10), SWCNT (10, 10) with divacancy, and 5-8-5 defects are 5.5, 4.1, and 4.9 GPa, respectively, while the values of Pc of the intrinsic SWCNT (17, 0), SWCNT (17, 0) with divacancy, and 5-8-5 defects are 0.4, 0.35, and 2.4 GPa, respectively. It is demonstrated that the divacancy defect can make the value of Pc of SWCNT (10, 10) decrease by 25.0% and make the value of Pc of SWCNT (17, 0) decrease by 12.5%, while 5-8-5 defect can make the value of Pc of SWCNT (10, 10) decrease by 11.0%. It is shown that divacancy defect can deteriorate the radial mechanical properties of SWCNTs while the 5-8-5 defect can alleviate the deterioration in their radial mechanical properties. To our surprise, the 5-8-5 defect can make the value of Pc of SWCNT (17, 0) increase by 500%. In other words, the 5-8-5 defect formed by saturating dangling bonds of divacancy defect can greatly enhance the radial mechanical properties of SWCNT (17, 0).
Based on the above discussion, the 5-8-5 defect in SWCNTs can enhance the mechanical properties of SWCNTs, which can be desired to improve the mechanical characteristics of SWCNT-based composite and also provide the mechanical stability for electric nano-circuit formed by SWCNTs with covalent inter-tube junctions.
Chirality, divacancy, and 5-8-5 defects have significant influence on the radial collapse of SWCNTs. The SWCNT capacity of resistance to collapse is directly related to its structure. It is recognized that the elementary unit of SWCNT is a six-member ring composed of six C− C bonds. The bending capacity of six C− C bonds along the bending direction should determine radial mechanical characteristics of SWCNT. Herein, a model is established to represent the bending capacity of six C− C bonds and further explain the SWCNT capacity of resistance to collapse.[31]
The bending directions of six C− C bonds in SWCNT (10, 10) and SWCNT (17, 0) upon loading are shown in Fig. 3. We define L as the projection of six C− C bond length along bending direction. L represents the bending capacity of six C− C bonds. In other words, the larger the L, the more difficultly the six C− C bond bends and the larger the value of Pc which the SWCNT is corresponding to will be.[31] It is easy to calculate the L1 (L of a six-member ring in SWCNT (10, 10)) = 5.728 Å > L2 (L of a six-member ring in SWCNT (17, 0)) = , 4.960 Å , which is demonstrated because the SWCNT (17, 0) is easier to bend and collapse than SWCNT (10, 10).
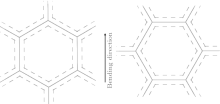 | Fig. 3. Bending directions of six C− C bonds in (a) SWCNT (10, 10) and (b) SWCNT (17, 0) upon loading. |
Now, the model is applied to the SWCNT with divacancy or 5-8-5 defects. Figure 4 shows the atomic networks of four six-member rings, corresponding to divacancy and 5-8-5 defects in SWCNT (10, 10) and SWCNT (17, 0). A divacancy defect is formed by deleting two carbon atoms of four six-membered rings, as shown in Figs. 4(c) and 4(d). The 5-8-5 defect can be formed by saturating dangling bonds of divacancy defect, as shown in Figs. 4(e) and 4(f). We can obtain the structures (b), (d), and (f) by rotating structures (a), (c), and (e) 30° towards the right. As shown in Table 3, it is calculated that La (L of four six-member rings in SWCNT (10, 10)) = 15.09 Å , Lb (L of four six-member rings in SWCNT (17, 0)) = 10.39 Å , Lc (L of corresponding divacancy defect in SWCNT (10, 10)) = 10.73 Å , Ld (L of corresponding divacancy defect in SWCNT (17, 0)) = 6.93 Å , and La > Lc, Lb > Ld, which indicates that the SWCNT with divacancy defect is easier to collapse.
It has been demonstrated that a variety of different polygons, such as hexagon, pentagon, and octagon are composed of sp2-hybridized carbon atoms.[46] Therefore, the current model should be applicable to SWCNTs with the 5-8-5 defect. Figure 5 shows the bond lengths and bond angles of the 5-8-5 defect structure which are marked by b1, b2, b3, b4, b5, and α , β , γ , φ , respectively. Therefore, the L of the 5-8-5 defect along bending direction can be calculated as follows.
In Fig. 4(e), Le (L of corresponding 5-8-5 defect in SWCNT (10, 10)) = 2b1cos(2π /3 − α /2) + 2b1sin(α /2 + π /6) + 2b2cos(4π /3 − β − α /2) + 2b2cos(β + α /2 − 7π /6) + 2b3cosπ /6 + 2b5cosπ /3 + 2b4cos(φ − π /3) + 2b4cos(φ − 2π /3) = 13.77 Å .
In Fig. 4(f), Lf (L of corresponding 5-8-5 defect in SWCNT (17, 0)) = 2b3 + 4b4cos(α /2) + 4b2sin(γ − π /2) + 4b4sin(φ − π /2) = 14.39 Å .
According to the above calculations, we can obtain La > Le > Lc and Lf > Lb > Ld, andPc(intrinsic SWCNT (10, 10)) (5.5 GPa) > Pc(SWCNT (10, 10) with 5-8-5) (4.9 GPa) > Pc(SWCNT (10, 10) with divacancy) (4.1 GPa)andPc(SWCNT (17, 0) with 5− 8− 5) (2.4 GPa) > Pc(intrinsic SWCNT (17, 0)) (0.4 GPa) > Pc(SWCNT (17, 0) with divacancy) (0.35 GPa).This indicates that the results are in good agreement with the law that the larger the value of L, the bigger the value of Pc of the corresponding SWCNT is, and therefore is the effect law of the familiar 5-7-7-5 defect on the radial collapse of SWCNT.[31] Based on the above discussion, it is demonstrated that our model is very applicable to the understanding of the influences of chirality and defect on radial mechanical properties of SWCNT. Therefore, the established model is very useful to guide the application of CNTs with detects in high-load composites.
In this paper, by using MM and MD simulations we investigate the effects of chirality, divacancy, and 5-8-5 defects on radial collapse and elasticity of SWCNT. It is shown that divacancy defect can deteriorate the radial mechanical properties of SWCNT while the 5-8-5 defect can enhance the radial mechanical properties of SWCNT (17, 0). The divacancy can make Pc of SWCNT (10, 10) decrease by 25.0% and make Pc of SWCNT (17, 0) decrease by 12.5%, while the 5-8-5 defect can make Pc of SWCNT (10, 10) decrease by 11.0%. However, the 5-8-5 defect can make Pc of SWCNT (17, 0) increase by 500%.
We introduce a valuable model for SWCNT deformed in the radial direction according to the project L of C− C bond along the bending direction. The model is validated for defect-free SWCNT and is then used to study the radial collapse of SWCNT with defects. The effects of chirality and defect on the radial collapse of SWCNT can be understood by the model. The strong sensitivities of radial collapse of SWCNT to chirality and defect can provide some significant guidance for high load structural applications of SWCNTs.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|