†Corresponding author. E-mail: anjan802002@yahoo.co.in
Very small nickel oxide nanoparticles were prepared by a sol–gel procedure using nickel nitrate hexahydrate and ammonium hydroxide as precursors. The particles are in the range of 5 nm–11 nm. The x-ray diffraction (XRD) crystallography and high resolution transmission electron microscopy (HRTEM) were employed to characterize the samples. They were found to be polycrystalline in nature and fcc (NaCl-type) in structure, with the lattice parameter varying with annealing temperature. HRTEM pictures show that the as-prepared samples are hexagonal in shape. Positron annihilation spectroscopy was used to investigate the Doppler-broadened spectra of the samples. The S and W parameters revealed that the chemical surroundings and momentum distribution of the vacancy clusters vary with crystallite size.
Nanomaterials are drawing much attention from scientists due to their different physical and chemical properties, particularly with changes in particle size.[1, 2] It is possible for structural and electrical properties of an atom cluster[3] or metal oxides to vary with crystallite size.[4] NiO is a p-type, wide band gap (bulk value 3.75 eV) semiconductor.[5] Several methods have been used to synthesize crystalline oxide powders and thin films at the nanometer scale.[6– 10] The main objectives are to reduce the cost of chemical synthesis and to produce materials for technological applications. Research is ongoing for undoped and doped[11] semiconductors to upgrade the performance of electronic devices to meet modern needs.[12– 17] Many researchers have synthesized NiO nanoparticles by various methods, such as sol– gel, surfactant-mediated synthesis, thermal decomposition, solvothermal techniques, and polymer-matrix assisted synthesis.[18– 20] Among those procedures the sol– gel method has some advantages, such as its simple process, low cost, and the ease of obtaining high purity products. Hence, it is quite promising and easy to use for industrial applications.
In this paper, we report the fabrication of nickel oxide (NiO) nanoparticles by a sol– gel method, followed by annealing at different temperatures and times to obtain various crystallite sizes. We also discuss the crystal structure and morphology of the resulting NiO nanoparticles. Positron annihilation spectroscopy has been carried out for defect characterization and to closely observe the core electron structure with the changes in particle sizes below 11 nm.
Various methods for the synthesis of NiO nanostructures with different types of morphologies and sizes have been reported by several authors.[21] In the present work we have adopted the sol– gel method to produce green samples of NiO nanoparticles. Twenty five grams of nickel nitrate hexahydrate (Ni(NO3)2· 6H2O) is dissolved in 150 ml of double distilled water and put in a magnetic stirrer. Then, 25% (v/v) ammonium hydroxide (NH4OH) is added slowly to precipitate out the light green nickel hydroxide. The precipitate was washed using distilled water to remove the excess salt and ammonia. One hundred seventy milliliters of ethanol (CH3– CH2– OH) is then added to the precipitate and stirred again, followed by the addition of 30-ml 1.01-N acetic acid (CH3– COOH). Stirring then continues for half an hour, and a clear green solution is obtained, which is heated mildly at 80 ° C and then dried in a furnace at 100 ° C to obtain NiO powder. It is thereafter annealed at different temperatures and times to obtain nanoparticles of different sizes.
To determine the particle size and strain of each sample, x-ray diffraction measurements of the samples were carried out with a Bruker D8 advance diffractometer using incident Cu Kα (λ = 1.5406 Å ) radiation at 40 kV and 40 mA. All of the samples were scanned from 2θ = 20° to 80° with a scanning speed of 2° per minute. The morphology and crystallite size of samples were studied by high-resolution transmission electron microscopy (HRTEM). The microscope used (FEI Model Technai S-twin) had a resolution 0.24 nm.
The source used to take coincidence Doppler broadening spectra (CDBS) was a strong 10 μ Ci 22Na deposited in solution form on a very thin (∼ 2 mg· cm− 2) Ni foil. It was dried and folded. The powdered sample was taken in a glass tube to immerse the foil. A vacuum C pump was used to remove the traces of trapped air in between the crystallites so that the powder could settle down under its own weight. The vacuum also kept the source and sample in dry and moisture-free conditions. For coincidence Doppler broadening spectroscopic (CDBS) measurements, two high purity germanium (HPGe) detectors of energy resolutions 1.27 keV and 1.33 keV at the positron annihilation gamma ray energy 511 keV were used to minimize the background effects. Sufficiently large numbers of counts (more than 107 in CDBS spectra) were acquired within a reasonable time with accurate calibration of the channels, and the spectra were analyzed using AMPS software.[22] The higher momentum distribution is perceived very clearly after background subtraction and peak normalization, with pure Ni taken as the reference standard sample.
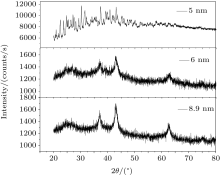
Figure 1 shows the x-Ray diffraction (XRD) spectrum of the samples. Our peaks agree well with the standard values (JCPDS Card No 71-1179), by which the purity of the samples is confirmed. All of the samples exhibited main peaks corresponding to the (111), (200), (220), (311), and (222) planes of face centred cubic structure. Secondary phases were generally absent in these spectra. The lattice constant of bulk NiO is 4.195 Å . From the XRD data we measured the lattice constant of each sample. We combined the Bragg’ s equation[23] with the lattice constant and Miller indices to get the relation
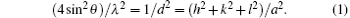
From the XRD data we can get θ (2θ is peak position), λ (wavelength used for XRD measurement) and h, k, l (the Miller indices of planes). From these, the value of the most intense peak lattice constant a was calculated. From the most intense broadened peak width, the average crystallite sizes of the different samples were estimated by using the Debye– Scherer equation, [24] and they varied from 5 nm to 10.47 nm. The Debye– Scherer equation is written as
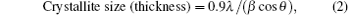
where β is the full width at half maximum (FWHM) of the most intense peak. Table 1 shows the crystallite sizes and their lattice constants.
| Table 1. Crystallite sizes of the annealed samples and their lattice constants. |
It can be seen from Table 1 that as particle size increases, the lattice constant also increases. For crystallite size 6.56 nm, a large increase occurs, but afterwards the lattice constant keeps a consistent trend. This fact can be attributed to the increasing defect concentration. The decrease of lattice parameter can result from strain induced by the increasing number of surface atoms (i.e. the atoms less surrounded by neighbor atoms) in an effort to minimize the surface free energy. Unlike in a bulk solid or coarse crystallite, where the number of core atoms far outnumber the surface atoms and offer stiff resistance to surface reduction, the inner core of a nanoparticle is soft enough to contract in order to facilitate the minimization of surface energy.
Figure 2 shows HRTEM images of some of the samples (Figs. 2(a) and 2(b)) and a simulated three-dimensional (3D) view of the NiO nanoparticles (Fig. 2(d)). The images show that the samples consist entirely of NiO nanocrystals of sizes about 5 nm and 10 nm. The crystallites are hexagonal and uniform in shape and size. The well developed lattice fringes shown in Fig. 2(c) show the high degree of crystallinity of our samples. The spacing of the two neighboring planes, for example, is about 0.24 nm in Fig. 2(c) and is consistent with the separation of the (111) planes in cubic (fcc) NiO.
The coincidence Doppler broadening measurements help to suggest the relative variation in the annihilation of positrons with electrons of the different elements present in a sample. The momentum conservation during the annihilation process gives a tool to study the momentum distribution of electrons in the solid. The momentum of the positrons after thermalization is significantly smaller than that of most electrons. An advantage of the momentum techniques is their sensitivity to the chemical environment of the annihilation site, which is higher than in positron lifetime spectroscopy. This occurs because the momentum distribution information is more influenced by the chemical surroundings than the electron density.[25] The W-parameter is the ratio of the counts in the wings of the curve of detected gamma radiation to the total, representing high-momentum core electrons. The S parameter is experimentally determined as the ratio of the counts in the central area of the 511-keV photo peak (| 511 keV − Eγ | ≤ 0.85 keV) and the total area of the photo peak (| 511 keV − Eγ | ≤ 4.25 keV). When a positron and an electron annihilate inside a defect of a material, two gamma rays are usually produced, of approximate energy 511 keV each. Gamma ray energy can be affected by the relative momentum of the particles. We have plotted the gamma photon versus channel number curve using the software AMPS. We have taken the total count of six consecutive channels on each wing of the curve to calculate the W parameter.
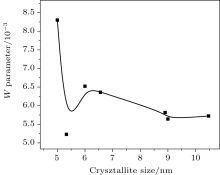
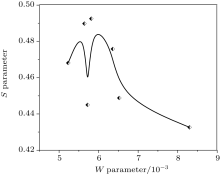
The plot between the W parameter and crystallite size is shown in Fig. 3. The W parameter reflects the contribution to positron annihilation of high-momentum core electrons surrounding a vacancy defect. We can see that the value of the W parameter is drastically reduced after 5 nm and saturates to a value of 0.0057. Contribution to annihilation of positrons by core electrons is reduced as crystallite size increases. This is to be expected. From the work of Hakala et al.[26] it has been shown that the W parameter decreases as vacancy clusters increase. This is also reflected in Table 1, where the increase in lattice constant with increased crystallite size indicates a structural transition. The observation is very significant from the point of view of the sensitivity of positrons to the charge states of the vacancies or their clusters. Normally, in order to be in the proximity of an Ni environment, the positrons have to reside in oxygen vacancies. This is, however, ruled out owing to their Coulomb repulsive interactions. The situation significantly changes if positron-trapping centers are vacancy clusters, either negatively charged or neutral. As the W parameter decreases, it is clear that with the increase of size, Ni2+ vacancies are also reduced in number. This can happen when a number of smaller vacancies are agglomerated to form a larger vacancy. This phenomenon is also reflected in our S– W plot (Fig. 4) where the S parameter increases to a value 0.4925 Å and then decreases to a lower value 0.43 Å . Thus the S parameter is higher if the relative contribution of lower-momentum electrons to positron annihilation is enhanced while the W parameter becomes greater if the contribution of the core electrons with higher momenta tends to increase.
With regard to the synthesis procedure, it is worth mentioning that the sol– gel protocol has succeeded in producing hexagonal NiO nanoparticles of sufficient purity and narrowly distributed sizes in the nanometer range of 5 nm to 11 nm. Study of NiO nanoparticles that are smaller than 11 nm is feasible through positron annihilation spectroscopy, which senses defects mostly at the surface. It was observed that S and W both increase upon reduction of crystallite size and then decrease, hence positron annihilation spectroscopy is very sensitive to the defect structures of different-sized nanoparticles.
The authors thank Dr. Goutam Das of National Metallurgical Laboratory, Jamshedpur for his great help in XRD and HRTEM characterization.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|