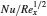After the classical work of Sakiadis^[1] many researchers have investigated the boundary layer flow over continuous moving surfaces. Such flows have been widely attractive to researchers due to their applications in industry and engineering. Recently, researchers have diverted their attention to the boundary layer flow of nanofluids. A liquid suspension containing ultrafine particles with a diameter less than 50 nm are known as a nanofluid. These ultrafine particles play a vital role in the heat transfer rate. Such particles greatly enhance the thermal conductivity, which also increases the heat transfer rate of the base fluid. This phenomenon is useful in many industrial, cooling, and biomedical applications, nuclear reactor, transportation industry, and micro-electromechanical systems. Commonly used nanoparticle materials are metal oxides, chemically stable metal, oxide ceramics, metal carbides, and metal nitrides whereas the base fluid includes water, ethylene-glycol, and other coolants, oil, and other lubricants, bio-fluids, polymer solutions, etc. Buongiorno^[2] found that the sum of base fluid velocity and slip velocity is the nanoparticles' absolute velocity. He focused on some active quantities, such as Brownian diffusion, thermophoresis, diffusiopharesis, Magnus effect, and fluid drainage. He concluded that Brownian diffusion and thermophoresis have significant effects on laminar flow. Many authors have since studied the Buongiorno model under different physical situations. For example, Hassani et al.^[3] analyzed the development of steady boundary layer flow subject to heat transfer and nanoparticle fraction. They considered the effects of Brownian motion and thermopharesis simultaneously. The flow and heat transfer in an incompressible viscous fluid near the three-dimensional stagnation point of a body are studied by Bachok et al.^[4] They considered a water-based nanofluid containing different types of nanoparticles, such as Cu, Al₂O₃ and TiO₂. The fully developed flow of an incompressible and thermodynamically compatible non-Newtonian third-grade nanofluid in coaxial cylinders has been investigated by Ellahi et al.^[5] They considered two illustrative models of variable viscosity, namely Reynolds's and Vogel's models. Pop et al.^[6] analyzed the steady mixed convection boundary-layer flow on a vertical circular cylinder embedded in a porous medium filled by a nanofluid. They investigated both cases of heated and cooled cylinders. They found a dual solution for the arising problem. Magnetohydrodynamic flow and heat transfer over a permeable stretching sheet in the presence of nanoparticles, slip condition, and thermal radiation are investigated by Ibrahim and Shankar.^[7] Moreover, they examined the combined effects of Brownian motion, thermophoresis parameter, and nanoparticle fraction. Ellahi^[8] presented the magnetohydrodynamic (MHD) flow of non-Newtonian nanofluid in a pipe. He considered the temperature-dependent viscosity. Zheng et al.^[9] investigated the flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in a porous medium. They considered the Brownian motion and thermophoresis in view of Rosselands' approximation. Turkyilmazoglu and Pop^[10] reported the heat and mass transfer of unsteady natural convection flow of nanofluids past a vertical infinite flat plate with a radiation effect. The boundary layer flow of a micropolar nanofluid and heat transfer over a vertical cylinder is reported by Rehman and Nadeem.^[11]

It is noticed that very scarce information is as yet available for the boundary layer flow of a nanofluid by a stretched cylinder.^{[12– 17]} Such investigations further narrowed down when non-Newtonian fluid with nanoparticles are considered. Hence, the objective of the present paper is to analyze the boundary layer flow and heat transfer of a Jeffrey nanofluid over a stretching cylinder. Thermal conductivity depends on temperature. Effects of Brownian motion and thermophoretic diffusion are analyzed. The homotopy analysis method (HAM)^{[18– 22]} is used to obtain the series solutions of nonlinear equations. Physical interpretation for various parameters of interest is made.

We consider the steady axisymmetric flow of an incompressible non-Newtonian fluid with nanoparticles. Constitutive equations of Jeffrey fluid^{[23– 27]} are employed. The contribution of the Brownian motion and thermophoretic diffusion of nanoparticles are observed. The flow is due to the stretching cylinder. Here r axis is taken normal to the x axis. The velocity, temperature, and concentration fields subject to boundary layer approximations are governed by the following equations

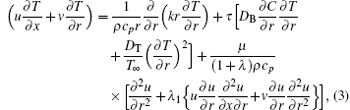
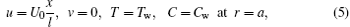
where u and v represent the velocity components along the x and r directions, respectively, U₀ is the reference velocity, λ is the ratio of relaxation to retardation times, λ ₁ is the retardation time, l is the characteristic length, τ = (ρ c)_p/(ρ c)_f is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid with ρ being the density, D_B is the Brownian diffusion coefficient, D_T is the thermophoretic diffusion coefficient, σ is the thermal diffusivity of the fluid, c_p is the specific heat at constant pressure, C_w is the concentration susceptibility, T_w is constant wall temperature, C_∞ is the concentration far away from the surface, and T_∞ is the ambient temperature. The variable thermal conductivity k is defined as

in which ε is the small parameter, k_∞ is the thermal conductivity of the fluid far away from the surface.

We introduce the similarity transformations in the forms

With the help of above transformations, equations (1) is identically satisfied and equations (2)– (5) yield the following equations

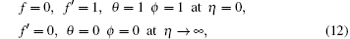
where β = λ ₂a is the Deborah number,

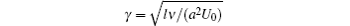
is the curvature parameter,

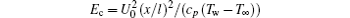
is the Eckert number, Pr = ρ C_pv/k_∞ is the Prandtl number, Le = v/D_B is the Lewis number, N_t = τ D_T (T_w – T_∞ ) / (T_∞ v) is the thermophoretic parameter, and N_b = τ D_B (C_w – C_∞ ) / v is the Brownian motion parameter. The local Nusselt number Nu_x is defined as

The local Sherwood number Sh_x is expressed by the following relation

where Re_x = ax²/v is the local Reynolds number.

Initial approximations and auxiliary linear operators are chosen as follows:

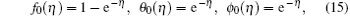
The above operators have the properties

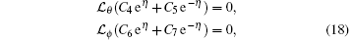
in which C_i (i = 1– 7) are the arbitrary constants determined from the boundary conditions. If p ∈ [0, 1] denotes an embedding parameter, ħ _f, ħ _θ , and ħ _ϕ the non-zero auxiliary parameters then the zeroth order deformation problems are represented by the following expressions

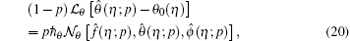
where the nonlinear operators , , and are defined by

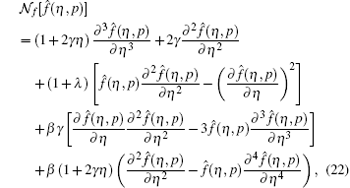
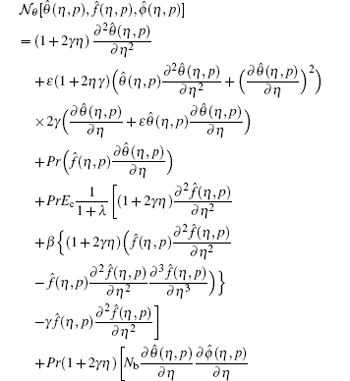
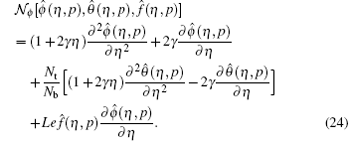
For p = 0 and p = 1 we have

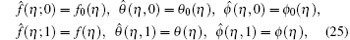
and when p variation is taken from 0 to 1 then f(η , p), θ (η , p), and ϕ (η , p) approach f₀(η ), θ ₀(η ), and ϕ ₀(η ) to f(η ), θ (η ), and ϕ (η ). Now f, θ , and ϕ in Taylor’ s series can be expanded as follows:

where the convergence depends upon ħ _f, ħ _θ , and ħ _ϕ . By a proper choice of ħ _f, ħ _θ , and ħ _ϕ the series (26)– (28) converge for p = 1 and hence

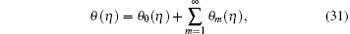
The m-th order deformation problems are

The general solutions of Eqs. (33)– (35) are

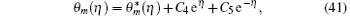
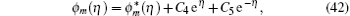
in which , , and are the particular solutions of Eqs. (33)– (35).

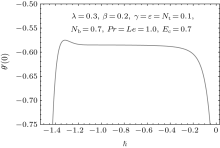
Convergence of a series solution strongly depends upon non-zero auxiliary parameters ħ _f, ħ _θ , and ħ _ϕ . For this purpose we plot the ħ curves for the velocity f″ (0), temperature θ ′ (0), and concentration ϕ ′ (0) fields. Figures 1– 3 depict the ħ curves for different values of physical parameters. The admissible ranges of ħ _f, ħ _θ , and ħ _ϕ are, respectively, given by − 1.2 < ħ _f < − 0.2, − 0.5 < ħ _θ < − 0.8, and − 0.8 < ħ _ϕ < − 1.2. It is found that the series solutions converge in the whole region of η when ħ _f = − 0.8, ħ _θ = − 1, and ħ _ϕ = − 1.2. Table 1 conforms the convergence of the HAM solution. It is obvious that 25-th-order approximations are sufficient for the convergent series solutions.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. ħ curve for velocity field.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. ħ curve for temperature field.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. ħ curve for concentration field.

Table 1.

Table 1.

Table 1. Convergence of HAM solutions for different orders of approximations. Order of approximations − f″ (0) − θ ′ (0) − ϕ ′ (0) 1 1.08533 0.6832 0.5829 5 1.07756 0.5910 0.5583 10 1.07722 0.5860 0.5502 15 1.07717 0.5852 0.5487 20 1.07716 0.5850 0.5483 25 1.07716 0.5850 0.5482 30 1.07716 0.5850 0.5482 40 1.07716 0.5850 0.5482 45 1.07716 0.5850 0.5482

Table 1. Convergence of HAM solutions for different orders of approximations.

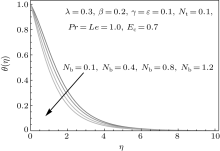
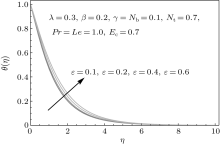
In this section the results of temperature and concentration fields are examined through graphs. The influence of λ is shown in Fig. 4. A larger λ leads to an increase in the temperature field and thermal boundary layer thickness. A variation in Deborah number β on temperature field is displayed in Fig. 5. As the Deborah number β increases the temperature field decreases. The behavior of temperature field for Brownian motion parameter N_b is plotted in Fig. 6. Brownian motion parameter decreases the temperature as well as thermal boundary layer thickness. Figure 7 indicates that the larger values of thermophoretic parameter N_t enhance the temperature field. A thermophoresis phenomenon is observed in motile particles motion where natural convection process is most significant. Figure 8 depicts the influence of curvature parameter on temperature field. For larger values of curvature parameter γ the temperature near the wall of cylinder decreases but after some large distance from the wall its value is increased. In addition, when η > 8 the temperature field approaches to zero asymptotically. Figure 9 shows the influence of ε on θ (η ). It is clearly seen from this figure that the increasing values of ε enhance the temperature profile. Figures 10 and 11 show the effects of Prandtl (Pr) and Eckert (E_c) numbers on the temperature field. A higher value of Pr reduces the temperature because a larger Prandtl number shows more viscous effects. The effect of Eckert number is more pronounced near the wall of the cylinder. When η > 3 the variation in Eckert number is insignificant and the temperature field approaches to zero asymptotically. In Fig. 12 we plot the temperature field against η for some values of Lewis number (Le). The Lewis number has a dual behavior on the temperature profile θ (η ). For small values of η , i.e., η < 2, the temperature decreases whereas for η > 3 the temperature increases. Figure 13 presents the influence of Brownian motion parameter N_b on the concentration field. The concentration field ϕ (η ) and associated boundary layer thickness are decreased when the Brownian motion parameter N_b increases. This is due to the fact that as Brownian motion parameter decreases the mass transfer rate as the surface increases. The effect of thermophoretic parameter on ϕ (η ) is displayed in Fig. 14. It is noticed that as N_t increases the concentration field increases. The curvature parameter γ increases the concentration field (see Fig. 15). Variation in γ is insignificant in the region η > 1 (i.e. near the wall of cylinder). Figure 16 shows the variation of Prandtl number on concentration field. Larger value of Pr decreases the concentration field. It is noticed from Fig. 17 that the concentration field decreases for larger Lewis number.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Influence of λ on temperature field.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Influence of β on temperature field.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Influence of Nb on temperature field.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Influence of Nt on temperature fields.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Influence of γ on temperature field.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Influence of ε on temperature field.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Influence of Pr on temperature field.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Influence of Ec on temperature field.

Fig. 12.

	Figure Option ViewDownloadNew Window
	Fig. 12. Influence of Le on temperature field.

Fig. 13.

	Figure Option ViewDownloadNew Window
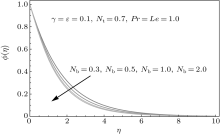	Fig. 13. Influence of Nb on concentration field.

Fig. 14.

	Figure Option ViewDownloadNew Window
	Fig. 14. Influence of Nt on concentration field.

Fig. 15.

	Figure Option ViewDownloadNew Window
	Fig. 15. Influence of γ on concentration field.

Fig. 16.

	Figure Option ViewDownloadNew Window
	Fig. 16. Influence of Pr on concentration fields.

Fig. 17.

	Figure Option ViewDownloadNew Window
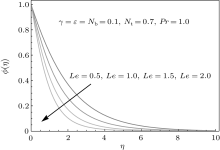	Fig. 17. Influence of Le on concentration fields.

In Table 2 the values of local Nusselt number are computed. The local Nusselt number θ ′ (0) being proportional to the slope of temperature at η = 0 increases with an increase in Pr, Le, and γ . It is found that | θ ′ (0)| also increases with an increase in λ . A slight variation in | θ ′ (0)| is noticed by increasing the Deborah number β . In addition, the magnitude of local Nusselt number increases when N_t is increased. Variable thermal conductivity increases | θ ′ (0)| . The magnitude of Sherwood number increases when Pr, Le, and E_c are enhanced (see Table 3). Thermophrosis and Brownian motion parameters have the opposite behavior on − ϕ (0).

Table 2.

Table 2.

Table 2. Values of local Nusselt number for different parameters. λ β ε Nb Nt γ Pr Le 0.0 0.2 0.1 0.1 0.7 0.1 1.0 0.7 0.5993 0.2 0.5893 0.4 0.5809 0.2 0.0 0.5809 0.1 0.5562 0.3 0.6129 0.2 0.0 0.6195 0.1 0.5850 0.3 0.5553 0.1 0.1 0.5850 0.2 0.4037 0.3 0.4429 0.7 0.1 0.5850 0.3 0.5072 0.4 0.4723 0.1 0.0 0.5441 0.1 0.5850 0.11 0.5892 1.0 0.5850 1.3 0.6354 1.8 0.6999 1.0 0.5850 1.2 0.6063 1.5 0.6321

Table 2. Values of local Nusselt number for different parameters.

Table 3.

Table 3.

Table 3. Values of local Sherwood number Sh for different parameters. γ Nb Nt ε Pr Ec Le − ϕ (0) 0.0 0.1 0.7 0.1 1.0 0.7 1.0 0.5221 0.1 0.7277 0.11 0.5507 0.1 0.1 0.6197 0.5 0.7196 0.9 0.7278 0.1 0.1 0.7277 0.2 0.5048 0.3 0.4702 0.7 0.0 0.5441 0.1 0.6197 0.2 0.5515 0.7 1.0 0.6197 1.2 0.6238 1.5 0.7270 1.0 0.0 0.5242 0.1 0.5310 0.5 0.5415 1.2 0.6242 1.5 0.7278 2.0 0.8798

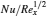Table 3. Values of local Sherwood number Sh for different parameters.

An investigation is carried out to study the boundary layer flow of non-Newtonian fluid containing nanoparticles. Here all of the physical properties of fluid are considered to be constant, except for thermal conductivity. The effects of fluid parameters λ and β on temperature fields are quite opposite. It is also found that the effect of variable thermal conductivity near the wall is more pronounced. Curvature parameter γ has a dual behavior on the temperature field. The effects of Brownian motion N_b and thermophoresis N_t parameters on the temperature and concentration fields are qualitatively similar. The Lewis number Le decreases the temperature field near the wall. The concentration field decays most rapidly for larger values of the Lewis number.