†Corresponding author. E-mail: xzliu@nju.edu.cn
*Project supported by the National Basic Research Program of China (Grant Nos. 2012CB921504 and 2011CB707902), the National Natural Science Foundation of China (Grant No. 11274166), the Fundamental Research Funds for the Central Universities, China (Grant Nos. 1113020403 and 1101020402), the State Key Laboratory of Acoustics, Chinese Academy of Sciences (Grant No. SKLA201401), the China Postdoctoral Science Foundation (Grant No. 2013M531313), the Priority Academic Program Development of Jiangsu Provincial Higher Education Institutions and Scientific Research Foundation for Returned Overseas Chinese Scholars, State Education Ministry, and the Project of Interdisciplinary Center of Nanjing University, China (Grant No. NJUDC2012004).
In view of the discrete characteristics of biological tissue, doublet mechanics has demonstrated its advantages in the mathematic description of tissue in terms of high frequency (> 10 MHz) ultrasound. In this paper, we take human breast biopsies as an example to study the influence of the internodal distance, a microscope parameter in biological tissue in doublet mechanics, on the sound velocity and attenuation by numerical simulation. The internodal distance causes the sound velocity and attenuation in biological tissue to change with the increase of frequency. The magnitude of such a change in pathological tissue is distinctly different from that in normal tissue, which can be used to differentiate pathological tissue from normal tissue and can depict the diseased tissue structure by obtaining the sound and attenuation distribution in the sample at high ultrasound frequency. A comparison of sensitivity between the doublet model and conventional continuum model is made, indicating that this is a new method of characterizing ultrasound tissue and diagnosing diseases.
With the development of ultrasonic technology, high frequency ultrasound has become increasingly popular in the fields of medicine, non-destructive testing, and many others. Biological tissue as an ultrasound medium is dispersive by nature, [1] that is, the sound velocity in tissue will increase as frequency increases. In medicine, when the ultrasonic frequency is tens of megahertz or higher, equivalently its wavelength is close to or smaller than a cell size (micron dimension), the frequency-dependent sound velocity becomes evident.[2– 9] Therefore, when high frequency ultrasound is used in the tissue characterization, the discrete characteristics of tissue become evident.
To solve the phenomenon that sound velocity changes with frequency, Ferrari et al. proposed the doublet mechanics (DM) theory in 1997, which is also called nanomechanics, to describe the discrete characteristics of the medium.[3] In the DM theory, the medium is composed of a series of discrete nodes, the distance of the double nodes is named internodal distance. The microscopic deformation between two nodes is characterized by M-order Taylor expansion. The order of M indicates the discrete degree of the medium rather than the precision of the mathematics. When M = 1, only the first order of the Taylor expansion is used, it reduces to the classical continuum mechanics (CCM), and the system described by DM becomes a pure continuous system that does not have a discrete nature at all. The results obtained from DM (M = 1) completely accord with those predicted by CCM. When M = ∞ , it corresponds to a pure single crystal that has a regular and periodic lattice structure. The success of ultrasonic applications in the characterization of the elastic properties of tissue shows that DM is quite powerful in the description of wave propagation in a partially discrete and granular material. For example, in 2002, Liu and Ferrari carried out frozen thin slice experiments of breast tissue (the frequency is 10 MHz) with CCM and DM models, respectively, and found that the data under the theory of DM were more reliable.[4] In 2004, Wu et al., [5] and Layman and Wu[6] studied the theory of a multi-scale equation in DM and revealed that when the discrete factor M = 2, the results of the theory were most agreeable to the experimental results, and they used the discrete model to simulate the longitudinal wave reflection coefficients in the diseased tissue. In 2009, Jiang et al. put forward the attenuation theory in DM and experimentally verified the modified DM theory of the reflection coefficient in multilayer tissues.[7, 8] In 2014, Ouyang et al. made an ultrasonic research on skin cancer.[9] Due to the fact that the penetration ability is weak for high frequency ultrasound, the high frequency ultrasound is most suitable for studying the surface tissue. However, the potential applications of DM, such as ultrasound imaging of biological tissue, are still in their infancy, and its potential applications need to be explored and developed further.
In previous studies, the pathological tissue was considered as the layered structure and each layer had a constant value of internodal distance.[4, 6– 9] In this paper, we take human breast biopsies as an example and assume that the internodal distance continuously changes. Our goal is to seek the differences in sound velocity and attenuation between pathological tissue and normal tissue due to variation of the internodal distance. The main reason that tissue is considered as being homogeneous is that our goal in this paper is to explore the ultrasound characteristics on superficial tissue or biopsy. Whether normal tissue is used or diseased tissue is adopted, a small piece of relatively homogeneous section or biopsy is always picked up and studied. By acknowledging the fact that at the early stage of the tissue lesions (such as lesion 10%∼ 50%), the change of some physical parameters maybe small but the change of the internodal distance can be large, [4] we also improve the accuracy of calculation by increasing the frequency of the ultrasound in our simulation through the distributions of the sound velocity and attenuation. We demonstrate that information about the internodal distance of the biological tissue can be obtained through the distributions of the sound velocity and attenuation.
In DM theory, the fundamental structure of biological tissue is comprised of a series of nodes and each node is surrounded by six nodes. The distance between a node and its adjacent node is called the internodal distance η α (α = 1, 2, … , 6). For biological tissue, the internodal distance describes the distance between cells. For simplicity, it is assumed that η α = η .
When an acoustic wave is incident upon a medium, the wave equation in the medium is given by[5]

where
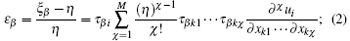
M is the discrete degree of materials; Aα β is the microlevel elastic modulus, which is composed of a 6 × 6 matrix, and is expressed as

with A11 = λ + 4μ , A12 = λ + μ , A44 = 4μ , A15 = − 2μ , λ , and μ being the lame coefficients of the medium; τ is a 6 × 3 matrix expressed by six directional cosine unit vectors, as follows:
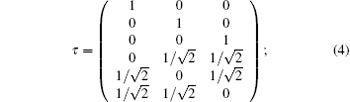
each subscript of k1, … , kχ and i run through the integers 1, 2, 3 corresponding to three-dimensional Cartesian coordinates; ρ is the density of the material; ui1 is the displacement of the wave along the direction xi.
When a longitudinal wave propagates along the direction x1, we have
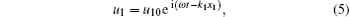
where u10 is the amplitude of the wave, ω is the angular frequency, and k1 is the wave number.
By substituting Eq. (5) into Eq. (1), we can obtain
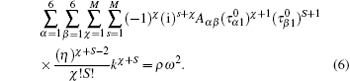
From Eq. (6) we obtain the sound velocity from the DM model as follows:

When M = 1,
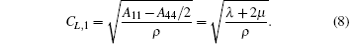
When M = 2,
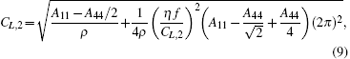
where f is the frequency. When M = 1, it reduces to CCM. When M = 2, the dispersion relation from Eq. (9) accords well with the experimental result.[5] So for biological tissue, we may always assume M = 2.
The relationships of Lame coefficients λ and μ each with Young’ s modulus E and Poisson’ s ratio σ are

When pathological tissue appears, the physical parameters of the tissue, such as Young’ s modulus or Poisson’ s ratio, may change. Therefore, the sound velocities in the malignant tissue and normal tissue are different. However, in some cases, the changes of Young’ s modulus and Poisson’ s ratio are both small and the sound velocity in biological tissue changes a little from the CCM model. However, we can find that the sound velocity in the tissue is a function of not only physical parameters, such as Lame coefficient, Young’ s modulus or Poisson’ s ration, but also frequency and the internodal distance. If the ultrasound frequency is high and the change of the internodal distance is large, then the change of the sound velocity is large from DM model.
Considering the fact that the attenuation in biological tissue is mainly due to the viscous damping, the wave equation with considering the attenuation in DM model is[7]
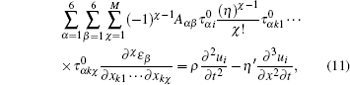
where k = k1 + iα is the viscous damping coefficient in the tissue.
From Eq. (11), we can obtain that the wave number k = k1 + iα , where k1 = ω /CL, 2 is the wave number and α is the attenuation coefficient.
In previous studies, it was assumed that the changes of internodal distances of normal and pathological tissues were discrete. Now for the case close to reality we assume that the internodal distance changes gradually in directions x2 and x3, where the x2– x3 plane is perpendicular to the direction x1 while the internodal distance is a constant along the direction of wave propagation x1 on condition that the thickness of the tissue sample is thin. Considering the fact that the high frequency (about 50 MHz) ultrasonic attenuation is high (about 40 dB/mm), the assumption of a thin sample is reasonable.
In the simulation, the parameters in malignant and normal human breast tissues are shown in Table 1 from Ref. [4]. In the table, lesion 1 represents 10% of the whole process of the lesion, lesion 2 denotes 50%, and lesion 3 refers to 100%.
Firstly, from the numerical calculations of Eq. (7), we can obtain the relationships between sound velocity and internodal distance at different frequencies in normal breast tissue, which are shown in Fig. 1</p>
 | Fig. 1. Variations of sound velocity with internodal distance at different frequencies in breast tissue. |
| Table 1. Values for physical parameters in malignant tissue and normal tissues. |
From Fig. 1, we can find that the sound velocity changes with the internodal distance: the larger the internodal distance or the greater the frequency, the greater the sound velocity becomes. For example, when the internodal distance changes from 1 μ m to 5 μ m, the sound speeds change by 4.87%, 26.86%, and 49.13%, respectively, at 10 MHz, 30 MHz, and 50 MHz. So at a certain frequency, we can obtain the information about the internodal distance through measuring the sound velocity. Figure 2 shows the variations of sound velocity with frequency at different degrees of pathological tissues compared with the case of normal tissue.
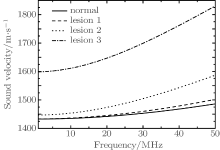 | Fig. 2. Variations of sound velocity with frequency at different degrees of pathological tissues compared with the case of normal tissue. |
In Fig. 2, when a 10% lesion process occurs, such as lesion 1, it is difficult to distinguish the difference in sound velocity between normal part and pathological part (about 15.81 m/s at 50 MHz). When an about 50% lesion process happens, the difference in sound velocity between normal and pathological part is also not obvious at low frequency (about 18.64 m/s at 10 MHz). However, as the frequency increases, the difference becomes more evident (about 50.44 m/s and 101.03 m/s at 30 MHz and 50 MHz, respectively). So through a comparison of sound velocity between the two parts at high frequency we can judge which part is pathological tissue. But in CCM theory, when the lesion reaches 50%, the difference is 13.58 m/s and does not change with the frequency. So it is difficult to distinguish the pathological part from the normal part.
From the above analysis, we calculate the sound velocity distribution for a 4 cm × 4 cm tissue containing a malignant part by using the data in Table 1. The center of lesion (the most serious disease point) has 50% of the whole process, corresponding to lesion 2 in Table 1. The distribution of physical parameters from normal point to the central point of the tissue follows discrete Gauss distribution in order to show the gradual distribution in reality. Figure 3(a) shows the distribution of the sound velocity difference (the difference in sound velocity between pathological point and normal one) from the CCM model. Figures 3(b) and 3(c) display the distributions of the sound velocity difference from the DM model at 10 MHz and 50 MHz, respectively. In Fig. 3(a) the change of velocity is little, less than 20 m/s. In Fig. 3(b) the change of velocity is about 50 m/s, a bit more obvious than in Fig. 3(a), but it is also hard to distinguish. When the frequency is 50 MHz, the change of velocity is obvious in Fig. 3(c), the malignant part is observable. The results are in agreement with the experimental results in kidney and liver, [10, 11] where the sound velocities of the normal and pathological tissues are obviously different at high frequency.
 | Fig. 3. Distributions of sound velocity increase predicted by (a) CCM model, DM model for (b) 10 MHz, and (c) 50 MHz. |
Like the sound velocity, sound attenuation is also a parameter that responds to internodal distance.[7] Figure 4 shows the variations of sound attenuation with the internodal distance at different frequencies. Here, in simulation the viscous damping coefficient is assumed to be η ′ = 0.25.[12] We can find the sound attenuation decreases with the increase of the internodal distance. At high frequency, such as 50 MHz, the attenuation reduces 97.69% but the attenuation under 10 MHz only changes 30.34% when the internodal distance changes from 0 μ m to 10 μ m. So in the normal tissue (the internodal distance is about 2.6 μ m), the decrement of sound amplitude is weaker than that in pathological tissue (the internodal distance is about 6.5 μ m). This is a new way to distinguish the internodal distance between normal and abnormal tissue.
Figure 5 is the simulation result of tissues with a dot lesion part when the frequency is 50 MHz. The reasons why 50-MHz frequency is used in this study are as follows: (i) when the frequency increases, the differences in velocity and attenuation between normal tissue and abnormal tissue are more obvious and the imaging result is clearer (as shown in Fig. 3(c)); and, (ii) this paper focuses mainly on the ultrasound characteristics of superficial tissue or biopsy. No thick penetration depth is required in the study. From Fig. 2, we can see when the frequency is 10 MHz, the difference in sound velocity is small, but when the frequency is 50 MHz the internodal distance η plays an important role in sound velocity. So the change of velocity at high frequency can be used to predict the internodal distance. The parameters in the center of the pathological parts are assumed to be the same as those of lesion 2. The distribution of physical parameters from normal point to the central point of the tissue also follows the discrete Gauss distribution. Figure 5(a) shows the setting structure of the internodal distance distribution with dot lesions. Figures 5(b) and 5(c) display the distributions of sound velocity and attenuation difference from calculation, respectively. From the images of simulation, we can see that the calculation results of the sound velocity and attenuation distributions are in consistence with the original lesion structure with background noise.
In this paper, we show that the microscopic structure information can be obtained from the sound velocity and attenuation changes of high frequency ultrasound based on the DM model, which is useful for the early detection of pathological tissues. Therefore, this method provides a new way to characterize the biological tissue. This method will be further verified experimentally in the near future.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|




