Cite this Article
Chen Yong, Huang Yi-Yong, Chen Xiao-Qian, Bai Yu-Zhu, Tan Xiao-Dong. Axisymmetric wave propagation in gas shear flow confined by a rigid-walled pipeline* . Chinese Physics B, 2015, 24(4): 044301  
Permissions
Axisymmetric wave propagation in gas shear flow confined by a rigid-walled pipeline*
Chen Yonga)†, Huang Yi-Yonga), Chen Xiao-Qiana), Bai Yu-Zhua), Tan Xiao-Dongb)
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China
Department of Electronic Technology, Officer’s College of CAPF, Chengdu 610213, China

†Corresponding author. E-mail: literature.chen@gmail.com

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11404405, 91216201, 51205403, and 11302253).

Abstract

The axisymmetric acoustic wave propagating in a perfect gas with a shear pipeline flow confined by a circular rigid wall is investigated. The governing equations of non-isentropic and isentropic acoustic assumptions are mathematically deduced while the constraint of Zwikker and Kosten is relaxed. An iterative method based on the Fourier–Bessel theory is proposed to semi-analytically solve the proposed models. A comparison of numerical results with literature contributions validates the present contribution. Meanwhile, the features of some high-order transverse modes, which cannot be analyzed based on the Zwikker and Kosten theory, are analyzed

Keyword: 43.28.Kt; 43.28.Ra; 43.28.Py; 43.28.Bj; wave propagation; shear flow; thermoviscous gas; Fourier–Bessel theory
1. Introduction

Wave propagation[1– 4] in perfect gas confined by a circular pipeline is of great interest in many industrial applications, such as noise damping in engines, [5] and catalytic converter design in exhaust silencers.[6, 7] While wave propagation in an inviscid fluid has been comprehensively analyzed, [8– 10] there is no complete theory, to the knowledge of the authors, that can be used to analyze the effects of viscous damping and thermal conduction[11, 12] on an acoustic wave in the presence of a moving fluid.

In the case of a stationary gas, Kirchhoff first proposed a complex transcendental equation considering the influences of fluid viscosity and thermal conductivity. Tijdeman[13] gave a numerical solution to the Kirchhoff formulation and summarized consecutive research work. Then, further research in this respect was carried out by Bruneau et al., [14] Stinson, [15] Anderson and Vaidya, [16] Karra and Tahar, [17] Liang and Scarton, [18] Beltman, [19] and so on.

In the case of a uniform mean flow, Dokumaci[20– 22] presented a quasi-analytical solution to the axisymmetric acoustic wave in the presence of the thermoviscous effect based on the assumption of Zwikker and Kosten.[13] Using the same simplifications, Peat[6] analyzed the non-isentropic and isentropic acoustic waves propagating in the laminar flow. Consecutive numerical solutions to the viscothermal acoustic wave were developed by Jeong and IH, [23] Astley and Cummings, [24] IH et al., [25] and Willatzen.[26] Furthermore, the influence of the axial temperature gradient was studied by Peat[27] and Peat and Kirby.[7] Recently, the features of wave propagation under the effects of thermoviscous property and eddy viscous damping in the turbulent boundary layer were analyzed by Knutsson and Abom.[28]

Since the theory of Zwikker and Kosten is valid under the low reduced frequency assumption where only the fundamental acoustic mode exists, [28] the previously mentioned models cannot describe the cases where high-order acoustic modes exist. The purpose of this paper is to relax the constraint of Zwikker and Kosten, and to present an improved acoustic model with respect to the acoustic velocity and temperature in the presence of a shear mean flow. Based on the conservations of mass, momentum, and energy, the governing equations are mathematically formulated into a set of second-order differential equations in terms of the velocity and temperature disturbances. Furthermore, the governing equations of an isentropic acoustic wave are provided by neglecting the change of the acoustic temperature, which leads to a set of second-order differential equations in terms of the velocity perturbance.

In the case of a liquid flow, the authors proposed an iterative method based on the Fourier– Bessel theory[29] to semi-analytically solve the isentropic acoustic wave propagating in a uniform flow[30– 32] and shear flow[33] considering the viscous dissipation, while the thermal conduction was neglected. Furthermore, the features of a longitudinal acoustic wave affected by the thermoviscous dissipation were analyzed in the shear flow in the cases without a temperature gradient[34] and with a constant axial temperature gradient, [35] respectively. In previous studies, [34, 35] the rotational velocity component caused by the shear vorticity mode was neglected and the disturbance was assumed to be a potential. Based on the Fourier– Bessel method, the authors[36] proposed an acoustic propagation model in terms of the acoustic velocity and temperature by considering the vorticity, entropy, and acoustic modes existing in the uniform gas flow. The present paper concentrates on the effects of thermoviscous dissipation and shear flow profile on wave propagation in gas pipeline flow. Meanwhile, a comparison between the isentropic and non-isentropic assumptions is addressed.

The rest of the present paper is organized as follows. In Section 2 the mathematical formulations of the governing equations of wave propagation are addressed. In Section 3, the solutions to the problems based on the Fourier– Bessel theory are detailed. In Section 4, some numerical analyses are presented, and finally some conclusions are drawn in Section  5.

2. Governing equations

An axisymmetric acoustic wave is assumed to propagate in a compressible homogenous gas moving through a rigid-walled pipeline, as shown in Fig.  1. The steady flow is assumed to be axially sheared, neglecting the effect of swirls. Wave propagation is assumed to be axisymmetric and the induced disturbances to the fluid pressure (p), flow velocity (υ ), density (ρ ), and temperature (T) satisfy linear approximations.

Fig.  1. Configuration of a circular rigid-walled pipeline in the cylindrical coordinate system with r, θ , and z being the radial, circumferential, and axial directions respectively. The pipeline radius and wall temperature are denoted by R and Twall, respectively, with ν 0 (r) being the shear flow profile.

2.1. Non-isentropic acoustic wave

Mathematical deduction starts from the conservations of mass, momentum, and energy, [6, 13, 35] expressed by

where η and κ th are the coefficients of the shear viscosity and thermal conductivity, respectively, and δ mn denotes the Kronecker delta function. When a linear wave propagates along the fluid, the physical variables become the sum of the steady-state components (denoted by subscript “ 0” ) and the first-order acoustic quantities (denoted by superscript), i.e.,

In the configurations of a constant steady density (ρ 0 = constant) and a shear flow with υ 0 = [0, 0, v0(r)], the steady fluid satisfies

In Refs.  [7] and [27], the authors considered the effect of a linear axial temperature gradient on wave propagation. However, in the present paper the temperature gradient is neglected and then the assumption is made that: ∂ T0/ ∂ z = 0, thus the steady temperature satisfies

Using the Taylor expansions of Eqs.  (1)– (3) and neglecting the products of fluctuating quantities gives

where the constraints shown in Eqs.  (5) and (6) have been used. If the acoustic wave is considered to be harmonic and axisymmetric, the acoustic perturbations may be taken in the form of exp [i (ω t − k0Kz)], where ω , K, and k0 = ω /c0 are the angular acoustic frequency, the dimensionless axial wavenumber, and the inviscid wavenumber, respectively. The symbol c0 is defined by 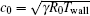with γ being the ratio of specific heat coefficients. Through the definition of the flow Mach number with M(r) = v0(r)/c0, the above equations can be simplified into

According to the state equation of the perfect gas with p = ρ R0T, one obtains

Inserting this equation into Eqs.  (12) and (13), respectively, gives

where the term (υ 0· ∇ )T0 vanishes as ∂ T0/∂ z = 0.

Since the circumferential component is neglected under the assumption of an axisymmetric acoustic wave, the radial (v′ r) and axial (v′ z) components of the acoustic velocity are considered. According to the separation-of-variables principle, the acoustic velocity and temperature can be expressed by

where the radial coordinate is non-dimensionalized by x = r/R. Substituting this expression into Eqs.  (15) and (16) yields

where the property in Eq.  (5) has been used. It should be noticed that the expansion is operated in the cylindrical coordinate while the circumferential component is neglected. By multiplying Eq.  (18) by (1 − KM)2, and Eq.  (19) by (1 − KM), respectively, we obtain

It can be found that the non-isentropic acoustic wave can be governed by coupled second-order differential equations in terms of the acoustic velocity and temperature, as shown in Eqs.  (21), (22), and (20).

2.2. Isentropic acoustic wave

In the case of isentropic acoustic assumption, the temperature disturbance is not taken into consideration. The governing equation of acoustic velocity (Eq.  (15)) is then simplified into

while the governing equation of acoustic temperature (Eq.  (16)) is neglected. As in the case of the non-isentropic acoustic wave, equation  (23) can be expanded into

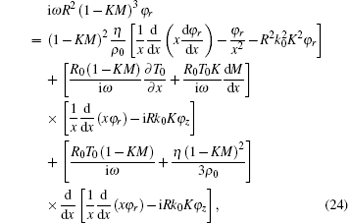
which is a set of coupled second-order differential equations in terms of the acoustic velocity [φ r (x), φ z (x)] and K.

2.3. Boundary condition

Since the wall is assumed to be rigid and isothermal, the acoustic temperature and axial velocity vanish. Furthermore, the influence of the fluid viscosity leads to the no-slip condition. Thus, one obtains

Due to the axisymmetric acoustic assumption, the radial particle velocity vanishes at the origin x = 0, leading to

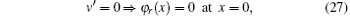
while φ z (x) and φ T (x) are bounded at x = 0.

3. Solution based on Fourier– Bessel theory

In what follows, we seek solutions based on the Fourier– Bessel theory[29] to the problems of the non-isentropic (Eqs.  (20), (21), and (22)) and isentropic (Eqs.  (24) and (25)) acoustic waves with the boundary constraints shown in Subsection  2.3. According to Eq.  (27), and the bounded values of the acoustic velocity and temperature in the interval x = [0, 1], one can express φ r, φ z, and φ T in terms of Fourier– Bessel sequences

where 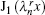and are Bessel functions of the first and zeroth orders, which are orthogonal and complete in the Lebesgue space . According to the boundary constraints in Eq.  (26), and are roots of the following Bessel functions

which shows that . Under the present constraints, the orthogonal properties of the Fourier– Bessel series are

If the specific functions φ r (x), φ z (x), and φ T (x) are presumed, the corresponding coefficients can be calculated by

which shows that the coefficients are independent of the radial coordinate.

3.1. Non-isentropic acoustic wave

In the case of a non-isentropic acoustic wave, substituting the Fourier– Bessel sequences of Eq.  (28) into Eqs.  (21), (22), and (20) yields

In the mathematical deduction, some properties of the Bessel function have been used, for which readers can referred to Ref.  [29] by Watson. Rearranging the terms in the above equations gives

By multiplying Eq.  (35) by , and Eqs.  (36) and (37) by and then integrating along the radial coordinate x ∈ [0, 1], we have

where the orthogonal properties of Fourier– Bessel sequences in Eq.  (30) have been used. In the above equations, we denote

In numerical calculation, if the number of orthogonal Fourier– Bessel functions in Eq.  (28) is N, expanding Eqs.  (37)– (39) results in a set of homogeneous linear algebraic equations

where (the superscript ‘ T’ means the operation of vector transpose) is the vector of the coefficients of Fourier– Bessel sequences. G(K) is a 3N × 3N matrix whose elements each are a function of K if M, R, and ω (= 2π f) are given while the steady temperature can be calculated by Eq.  (7). Since X does not vanish simultaneously according to Eq.  (28), the non-trivial solution to Eq.  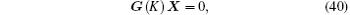(41) is the vanishing of the corresponding determinant, i.e.,

which can be solved by various numerical iterative methods. It should be noticed that the vector X cannot be obtained and a comprehensive explanation can be found in Refs.  [10] and [30] by Chen et al.

3.2. Isentropic acoustic wave

In the case of the isentropic acoustic wave, substituting Eq.  (28) into Eqs.  (24) and (25) yields

Rearranging the terms in the above equations gives

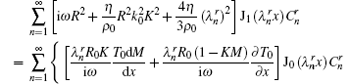
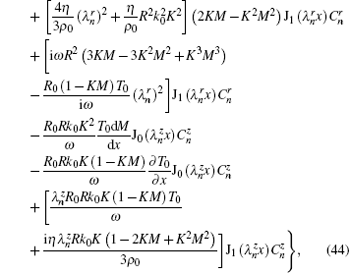
By multiplying Eq.  (45) by and Eq.  (46) by and then integrating along the radial coordinate x ∈ [0, 1], we have

The above-mentioned symbols are identical to the case of the non-isentropic acoustic wave. Furthermore, the axial wavenumber K can be solved using the same procedure as those shown in Subsection  3.1.

4. Zwikker and Kosten approximation

Adopting the Zwikker and Kosten approximation, Peat[6] proposed the variational solutions to the non-isentropic and isentropic acoustic waves. Specifically, in the case of a non-isentropic acoustic wave, the axial dimensionless wavenumber K satisfies

where denotes the averaged Mach number. The governing equation of the isentropic acoustic wave is

On the other hand, Dokumaci[20, 22] proposed a solution to the fundamental wave propagating in the uniform flow based on the assumption of Zwikker and Kosten. Specifically, the governing function of a non-isentropic acoustic wave[36] is

where the symbol satisfies . In the case of an isentropic acoustic wave, the governing function is simplified into

5. Discussion

In what follows, wave propagation in the perfect gas is numerically studied. Since we assume ∂ T0/∂ z = 0, the steady temperature can be expressed by T0 = Twall + g(x), equation  (7) can then be simplified into

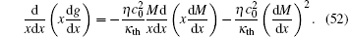
The shear flow profile is assumed to be laminar with , where is the averaged Mach number.

The constant parameters of the perfect gas are Twall = 1273  K (1000  ° C), γ = 1.4, ρ 0 = 0.35  kg/m3, cp = 1141  J/(kg · K), κ th = 0.0674  W/(K · m), R0 = 287 J/(kg · K), and η = 4.15 × 10− 5  kg/(s · m), which are the parameters of configuration considered by Dokumaci[22] and Astley and Cummings.[24] Numerical results are calculated in the case of N = 50 according to the previous research.[30] In the following analysis, particular considerations focus on the relative phase velocity (1/KR) and attenuation coefficient (A = | 8.686k0KI| : dB/m), where the subscripts ‘ R’ and ‘ I’ denote the real and imaginary components of K, respectively.

5.1. First acoustic mode

In applications where the theory of Zwikker and Kosten is adopted, many simplified models exist, two of which were listed in Section 4. In this subsection, the differences among these models and proposed model are analyzed under the assumption of R = 1  mm

In the case of a stationary gas with M = 0, figure  2 shows the plots of the relative phase velocity (Fig.  2(a)) and attenuation coefficient (Fig.  2(b)) versus acoustic frequency for the three models. Meanwhile, a comparison between the non-isentropic and isentropic acoustic assumptions is addressed. In the case of the isentropic acoustic wave, the relative phase velocity and attenuation coefficient are nearly identical between the model proposed by Dokumaci and that proposed by the authors, which validates the present work. As the acoustic frequency goes up, the differences in relative phase velocity and attenuation coefficient between the model proposed by Peat and the other two models become significant. A similar phenomenon can be found in Ref.  [22] by Dokumaci. In the case of the non-isentropic acoustic wave, the performance predicted by Peat model is the worst in the three models. As the acoustic frequency goes up, the difference between the Dokumaci's model and the authors' model becomes obvious. Physically speaking, the increase of acoustic frequency may trigger high-order modes (see Refs.  [30] and [35] for wave propagation in the liquid flow) propagating in the pipeline. The effect of the radial acoustic velocity becomes more important, thus the assumption of Zwikker and Kosten becomes increasingly controversial.

Fig.  2. Relative phase velocity (a) and attenuation coefficient (b) of the fundamental mode each as a function of the acoustic frequency for different models. ‘ nonisen’ refers to the non-isentropic acoustic wave, ‘ isen’ the isentropic acoustic wave, ‘ Peat’ the model proposed by Peat, ‘ Doku’ the model proposed by Dokumaci, and ‘ Prop’ the model proposed by the authors.

In the case of a moving fluid with averaged Mach number compared with the case of the stationary fluid, the relative phase velocity of the forward wave becomes larger while the relative phase velocity of the backward wave becomes smaller due to the effect of flow convection. On the other hand, the attenuation coefficient becomes smaller in the downstream propagation and larger in the upstream propagation. Unlike the case of the stationary fluid, the difference between the Dokumaci's mode and the authors' mode is obvious. With the increase of the acoustic frequency, such a difference becomes more significant. Since the model proposed by Dokumaci is based on the assumption of a uniform flow, the shear effect of the steady flow is not considered. On the other hand, the shear effect is taken into consideration in the model proposed by the authors.

Although the models proposed by Peat and Dokumaci may be reasonable candidates to describe wave propagation in some applications, prediction errors exist, as shown in Figs.  2– 4. Importantly, the two models are lacking in the ability to predict wave propagation in the presence of high-order transverse mode due to the constraints of theory of Zwikker and Kosten. However, the model proposed by the authors fills in the gap.

Fig.  3. Relative phase velocities (a) and attenuation coefficients (b) of the fundamental mode in the downstream propagation among different models. See Fig.  2 for the interpretation of the legends.

Fig.  4. Relative phase velocities (a) and attenuation coefficients (b) of the fundamental mode in the upstream propagation for different models. See Fig.  2 for the interpretation of the legends.

5.2. High-order acoustic modes

This subsection concentrates on the wave propagation when high-order acoustic modes exist with the configurations of the mean Mach number and pipeline radius R = 50  mm. Since the non-isentropic acoustic model is more physically valuable than the isentropic model, this subsection concentrates on the features of non-isentropic acoustic wave. Specifically, figure  5 illustrates the relative phase velocity of the second and third modes propagating forward (Fig.  5(a)) and backward (Fig.  5(b)) while figure  6 shows the attenuation coefficients in the downstream (Fig.  6(a)) and upstream (Fig.  6(b)) propagation.

With the increase of acoustic frequency, the relative phase velocity of each mode converges in both downstream and upstream propagation. From Figs.  2– 4, it can be seen that the relative phase velocity of the first mode goes up to converge. On the other hand, figure  5 shows the plots of the relative phase velocities of high-order modes (second and third modes) come down to converge. Furthermore, the existence of a high-order mode is determined by the acoustic frequency, which is called the cut-off frequency.[30]

Fig.  5. Effects of the acoustic frequency on the relative phase velocities of the second and third modes propagating in the downstream (a) and upstream (b) directions.

As shown in Figs.  2– 4, the attenuation coefficient of the first mode augments with the increase of the acoustic frequencies in both downstream and upstream propagations. The variations of the attenuation coefficients of the high-order modes (second and third modes) are complex, no matter what direction the mode propagates in. When the acoustic frequency is near the cut-off frequency of a specific mode, the attenuation coefficient becomes extremely large, reflecting the property of the cut-off– cut-on transition.[37, 38] With the increase of the acoustic frequency, the attenuation coefficient decreases dramatically but increases slowly in the end. The tendency of attenuation coefficient is more complicated in the upstream propagation than in the downstream propagation.

Fig.  6. Effects of acoustic frequency on the attenuation coefficient of the second and third modes propagating in the downstream (a) and upstream (b) directions.

6. Conclusions

This paper deals with the axisymmetric acoustic wave propagating in the perfect gas in the presence of a shear mean flow confined by a circular rigid-walled pipeline. Our particular purpose is to relax the constraint of Zwikker and Kosten, which is primarily used to simplify the analysis of the fundamental acoustic wave. Mathematical formulations of the non-isentropic and isentropic acoustic waves are deduced from the conservations of mass, momentum, and energy. A semi-analytical method based on the Fourier– Bessel theory is proposed, which is complete and orthogonal in the Lebesgue space. Numerical comparison between the proposed model and literature models reveals that the assumption of Zwikker and Kosten becomes increasingly controversial in the case of a larger acoustic frequency. Furthermore, the features of high-order acoustic modes are analyzed based on the non-isentropic acoustic model.

Reference
1 Zhang Y X, Jia J, Liu S G and Yan Y 2010 Chin. Phys. B 19 105202 DOI:10.1088/1674-1056/19/10/105202 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
2 Li W, Liu S B and Yang W 2010 Chin. Phys. B 19 030307 DOI:10.1088/1674-1056/19/3/030307 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
3 Wang D and Zhang M G Acta Phys. Sin. 63 069101 (in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
4 Wang Y Lin S Y and Zhang X L Acta Phys. Sin. 63 034301(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
5 Brambley E J, Darau M and Rienstra S W 2012 J. Fluid Mech. 710 545 DOI:10.1017/jfm.2012.376 [Cited within:1] [JCR: 1.415]
6 Peat K S 1994 J. Sound Vib. 175 475 DOI:10.1006/jsvi.1994.1340 [Cited within:4] [JCR: 1.613]
7 Peat K S and Kirby R 2000 J. Acoust. Soc. Am. 107 1859 DOI:10.1121/1.428466 [Cited within:3] [JCR: 1.646]
8 Chen Y, Huang Y, Chen X and Hu D 2014 Shock Vib. 2014 912404 DOI:10.1155/2014/912404 [Cited within:1] [JCR: 0.535]
9 Chen Y, Huang Y and Chen X 2013 Acta Acust. Acust. 99 503 DOI:10.3813/AAA.918630 [Cited within:1] [JCR: 0.714]
10 Chen Y, Huang Y and Chen X 2013 Commun. Nonlinear Sci. Numer. Simul. 18 3023 DOI:10.1016/j.cnsns.2013.04.011 [Cited within:2] [JCR: 2.773]
11 Yuan S W Feng Y H Wang X Zhang X X Acta Phys. Sin. 63 014402(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
12 Hui Z X He P F, Dai Y and Wu A H Acta Phys. Sin. 63 074401(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
13 Tijdeman H 1975 J. Sound Vib. 39 1 DOI:10.1016/S0022-460X(75)80206-9 [Cited within:3] [JCR: 1.613]
14 Bruneau M, Herzog P, Kergomard J and Polack J D 1989 Wave Motion 11 441 DOI:10.1016/0165-2125(89)90018-8 [Cited within:1] [JCR: 1.467]
15 Stinson M R 1991 J. Acoust. Soc. Am. 89 550 DOI:10.1121/1.400379 [Cited within:1] [JCR: 1.646]
16 Anderson M J and Vaidya P G 1991 J. Acoust. Soc. Am. 90 1056 DOI:10.1121/1.402294 [Cited within:1] [JCR: 1.646]
17 Karra C and Tahar M B 1997 J. Acoust. Soc. Am. 102 1311 DOI:10.1121/1.420050 [Cited within:1] [JCR: 1.646]
18 Liang P N and Scarton H A 1996 J. Sound Vib. 193 1099 DOI:10.1006/jsvi.1996.0335 [Cited within:1] [JCR: 1.613]
19 Beltman W. M 1999 J. Sound Vib. 227 555 DOI:10.1006/jsvi.1999.2355 [Cited within:1]
20 Dokumaci E 1995 J. Sound Vib. 182 799 DOI:10.1006/jsvi.1995.0233 [Cited within:2] [JCR: 1.613]
21 Dokumaci E 2001 J. Sound Vib. 240 637 DOI:10.1006/jsvi.2000.3254 [Cited within:1] [JCR: 1.613]
22 Dokumaci E 1998 J. Sound Vib. 210 375 DOI:10.1006/jsvi.1997.1336 [Cited within:4]
23 Jeong K W and IH J G 1996 J. Sound Vib. 198 67 DOI:10.1006/jsvi.1996.0557 [Cited within:1]
24 Astley R J and Cummings A 1995 J. Sound Vib. 188 635 DOI:10.1006/jsvi.1995.0616 [Cited within:2] [JCR: 1.613]
25 IH J G, Park C M and Kim H J 1996 J. Sound Vib. 190 163 DOI:10.1006/jsvi.1996.0054 [Cited within:1] [JCR: 1.613]
26 Willatzen M 2003 J. Sound Vib. 261 791 DOI:10.1016/S0022-460X(02)00990-2 [Cited within:1]
27 Peat K S 1997 J. Sound Vib. 203 855 DOI:10.1006/jsvi.1997.0917 [Cited within:2] [JCR: 1.613]
28 Knutsson M and Abom M 2010 J. Sound Vib. 329 4719 DOI:10.1016/j.jsv.2010.05.018 [Cited within:2] [JCR: 1.613]
29 Watson G N 1966 A Treatise on the Theory of Bessel Functions2nd edn. London Cambridge University Press 1 804 [Cited within:3]
30 Chen Y, Huang Y and Chen X 2013 J. Acoust. Soc. Am. 134 2619 DOI:10.1121/1.4818774 [Cited within:5] [JCR: 1.646]
31 Chen Y, Huang Y and Chen X 2013 Ultrasonics 53 595 DOI:10.1016/j.ultras.2012.10.005 [Cited within:1] [JCR: 2.028]
32 Chen Y, Huang Y, Chen X and Bai Y J. Acoust. Soc. Am. 136 [Cited within:1] [JCR: 1.646]
33 Chen Y, Huang Y, Chen X, Bai Y and Tan X 2014 Aerosp. Sci. Technol. 39 72 DOI:10.1016/j.ast.2014.08.013 [Cited within:1] [JCR: 0.873]
34 Chen Y, Huang Y and Chen X 2013 Acta Acust. Acust. 99 875 DOI:10.3813/AAA.918667 [Cited within:2] [JCR: 0.714]
35 Chen Y, Huang Y and Chen X 2013 J. Acoust. Soc. Am. 134 1863 DOI:10.1121/1.4816414 [Cited within:4] [JCR: 1.646]
36 Chen Y, Huang Y, Chen X and Hu D 2014 J. Comput. Acoust. 22 1450014 DOI:10.1142/S0218396X14500143 [Cited within:2] [JCR: 0.69]
37 Smith A F, Ovenden N C and Bowles R I 2012 Wave Motion 49 109 DOI:10.1016/j.wavemoti.2011.07.006 [Cited within:1] [JCR: 1.467]
38 Ovenden N C 2005 J. Sound Vib. 286 403 DOI:10.1016/j.jsv.2004.12.009 [Cited within:1] [JCR: 1.613]