Cite this Article
Keshavarz A†, Naseri M.. Propagation of Gaussian beams family through a Kerr-type left-handed metamaterial. Chinese Physics B, 2015, 24(4): 044207  
Permissions
Propagation of Gaussian beams family through a Kerr-type left-handed metamaterial
Keshavarz A†, Naseri M.
Department of Physics, Shiraz University of Technology, Shiraz, Iran

†Corresponding author. E-mail: Keshavarz@sutech.ac.ir

Abstract

In this paper the propagation of elegant Hermite-cosh-Gaussian, elegant Laguerre Gaussian, and Bessel Gaussian beams through a Kerr left-handed metamaterial (LHM) slab have been studied. A split-step Fourier method is used to investigate the propagation of laser beams through this media. Numerical simulation shows that Gaussian beams have different focusing behaviors in a Kerr LHM slab with positive or negative nonlinearity. Beam focusing happens in slabs with positive nonlinearity and not in slabs with negative nonlinearity; however, negative nonlinearity is required for a Kerr LHM slab to act like a lens. Additionally, the focusing properties of beams can be controlled by controlling the thickness of the slab or the input power of the incident beam. A multilayer structure is also proposed to have beam focusing by thinner slabs and passing longer distances.

Keyword: 42.65.-k; 78.67.Pt; 42.65.Jx; Kerr-type left-handed metamaterial; Gaussian beams family; split-step Fourier method
1. Introduction

Veselago considered media with negative electric permittivity and magnetic permeability for the first time in 1968.[1] Such a media is termed a “ left-handed” metamaterial (LHM), because the wave vector, electric field vector, and magnetic field vector form a left-handed triad. In this media the direction of phase velocity is anti-parallel to the energy flow in the media, thus the media could be assumed to have a negative refraction index. In the late 1990s, Pendry et al. presented methods to achieve negative permittivity and permeability, which led to the design of LHMs.[2] Subsequently, Smith et al. reported the first experimental implementation of such materials at microwave frequencies regime.[3]

The negative value of ε can be found naturally in metals and plasmas, therefore negative-ε metamaterials can be created by simple means, such as the addition of metallic rods or microplasmas.[4] For instance, recently a uniaxial plasma metamaterial that exhibits negative refraction is demonstrated in Ref.  [5]. Another structure for negative index material is a metal– dielectric– metal sandwiched metamaterial, [6] which has been widely investigated because of its remarkable properties.[7– 9]

LHMs can be used in a wide variety of applications, such as lenses, couplers, antenna, filters, absorbers, scattering composites, clocking, and so on.[10– 19] Because of their unique ability to guide electromagnetic waves, left-handed materials have been developed rapidly in recent years. For example, focusing of optical beams is possible in a flat LHM slab; however, in a conventional lens there should be a curved structure to focus the light.

Nonlinear metamaterials, due to their intensity-dependent effects, such as self-focusing, bistability, harmonic generation, and parametric amplification, have been the subject of many studies. A nonlinear metamaterial can be made of embedded split-ring resonators in a nonlinear media. Moreover, double-nonlinear metamaterial with both nonlinear electric and magnetic inclusions are proposed to show tunable nonlinear response with control over both electric and magnetic nonlinearities.[20]

The possibility of controlling the effective parameters of the metamaterial using nonlinearity has been suggested in Refs.  [21] and [22]. In nonlinear LHMs, interaction between diffraction and nonlinear effect is found contrary to that of either a conventional Kerr media or a linear LHM. Previously, Kerr-type LHMs have been found to have a great potential for application in the control of light beam propagation. The focusing properties of Gaussian beams by a Kerr LHM slab have been studied both analytically and numerically, and it has been found that the focusing properties of beams can be tuned by slab thickness, nonlinearity characteristics of media, and the input power of the Gaussian beam.[23]

In this paper the focusing behavior of other solutions of the Helmholtz equation, such as elegant-Hermite-cosh-Gaussian (EHChG), elegant Laguerre Gaussian (ELG), and Bessel Gaussian (BG) beams have been investigated. Using a numerical split-step Fourier method shows that a Kerr LHM slab with positive nonlinearity acts as a lens, and self-focusing happens inside a Kerr LHM slab with negative nonlinearity. In addition, a multilayer structure with subsequent right-handed (RHM) and LHM media is suggested and the beam propagation through this structure is studied.

2. Physical model

In a Kerr LHM slab the nonlinear Schrö dinger wave equation governs wave propagation behavior in the media, which is given by[24]

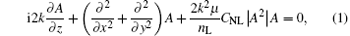
where k = nL2π /λ , nL is the linear refraction index of the LHM slab, A is the complex envelope of the electric field, CNL = χ /2nL is the nonlinear coefficient, χ is the cubic susceptibility, μ is the magnetic permeability of the LHM slab.

The split step Fourier method is a computational technique that is used in electromagnetics to solve the paraxial wave equation under slowly varying envelope approximation, for both linear and nonlinear equations.[25] We use this numerical method to investigate the propagation behavior of EHChG, ELG, and BG beams in our concerned media by replacing the field distribution of beams in Eq.  (1) and solving the equation for x and y variables.

3. Gaussian beam family

The field distribution of two-dimensional EHChG beams have the following field distribution at the waist plane:[26]

where Hm and Hn are, respectively, m-order and n-order Hermite functions. E0 is the beam amplitude at the central position of z = 0, Ω 0x and Ω 0y are the parameters associated with the hyperbolic cosine function in x and y directions, respectively. ω 0x and ω 0x are the waist of Gaussian beam in transverse coordinates.

The field distribution of two-dimensional ELG beams at the plane of z = 0 is given by[27]

where 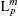is the Laguerre polynomial, m and p are mode orders, E0 is the beam amplitude at the central position of z = 0, ω 0x and ω 0y are the waist of the Gaussian beam in a transverse coordinate.

The field distribution of two-dimensional Bessel– Gaussian beams at the plane z = 0 is given by[28]

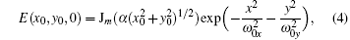
where Jm is the Bessel function of the first kind, α is a constant, m is the mode order of the beam, E0 is the beam amplitude at the central position of z = 0, ω 0x and ω 0y are the waist of the Gaussian beam in transverse coordinates.

4. Simulation and discussion

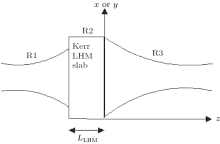
Consider a laser beam, propagating through a Kerr LHM slab, as shown in Fig.  1. The beam propagates from free space (region R1) through Kerr LHM slab (region R2) with thickness LLHM, and then passes to another free space (region R3). In addition, the beam waist is assumed to be located at z = − LLHM, which is the left border of the Kerr LHM slab.

Fig.  1. Schematic configuration of Gaussian beam propagation through a Kerr LHM slab.

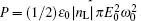
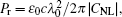
The incident beam power and the reference power are defined as and , respectively. Where E0 and ω 0 are the peak amplitude and spot radius at the beam waist. The ratio of incident beam power and critical power is defined as Rp = P/Pr, and the following parameters have been chosen for the incident beams profile and the slab: λ 0 = 1053  nm, ω 0x = ω 0y = 0.4  mm, μ = − 1, and n = − 1.

4.1. Beam propagation in a linear LHM media

First, we consider a linear LHM media. Incident beam waist radius increases by propagating through LHM slab, R2, and then decreases by propagating in the next free space, R3. In this case, the waist of the focused beam cannot be smaller than the incident beam waist.

Figure  2(a) shows the transverse field distribution of the EHChG beam in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. Figure  3(a) shows the transverse field distribution of the BG beam in a slab with LLHM = 7  cm at z = 0 and z = 7  cm, in the first row and the second row, respectively. Figure  4(a) shows the transverse field distribution of the ELG beam in a slab with LLHM = 5  cm at z = 0 and z = 5  cm, in the first row and the second row, respectively.

Fig.  2. The transverse field distribution of the EHChG beam with m = n = 2, at the end of R2 and R3, in the first row and the second row, respectively; column  (a) for χ = 0, LLHM = 10  cm, and z = 10  cm; column  (b) for χ > 0, Rp = 1.15, LLHM = 20  cm, and z= 20  cm; column  (c) for χ > 0, Rp = 1.15, LLHM = 10  cm, and z = 10  cm; column  (d) for χ > 0, Rp = 0.5, LLHM = 10  cm, and z = 10  cm; column  (e) for χ < 0, Rp = 1.15, LLHM = 10  cm, and z = 10  cm; column  (f) for χ < 0, Rp = 2.3, LLHM = 20  cm, and z = 20  cm.

Fig.  3. The transverse field distribution of the BG beam with m = 2 at the end of R2 and R3, in the first row and the second row, respectively; column  (a) for χ = 0, LLHM = 7, and z = 7  cm; column  (b) for χ > 0, Rp = 5, LLHM = 10  cm, and z = 10  cm; column  (c) for χ > 0, Rp= 1.15, LLHM = 10  cm, and z = 10  cm; column  (d) for χ > 0, Rp = 0.5, LLHM = 10  cm, and z = 10  cm; column  (e) for χ < 0, Rp = 10, LLHM = 3  cm, and z = 3  cm; column  (f) for χ < 0, Rp = 10, LLHM = 5  cm, and z = 5  cm.

Fig.  4. The electric field distribution of the ELG beam with m = n = 2 at the end of R2 and R3, in the first row and the second row, respectively; column  (a) for χ = 0, LLHM = 5  cm, and z= 5  cm; column  (b) for χ > 0, Rp = 10, LLHM = 5  cm, and z = 5  cm; column  (c) for χ > 0, Rp = 10, LLHM = 7  cm, and z = 7  cm; column  (d) for χ > 0, Rp = 0.5, LLHM = 7  cm, and z = 7  cm; column  (e) for χ < 0, Rp = 10, LLHM = 7  cm, and z = 7  cm; column  (f) for χ < 0, Rp = 5, LLHM = 7  cm, and z = 7  cm.

In these three cases, the self-focusing happens in R3 and the laser beam transverse field at z is the same as the incident beam.

4.2. Beam propagation in a nonlinear LHM media

Now a nonlinear LHM media is considered in two cases: χ > 0 and χ < 0. It has been found out that, for χ > 0 the beam diverges when propagating through the Kerr LHM slab. Then, focusing happens when propagating through R3. In this case, the beam waist of the focused beam can be smaller than the incident beam waist, which does not happen in a linear LHM media, as mentioned earlier.

Figure  2(b) shows the transverse field distribution of the EHChG beam with Rp = 1.15 in a slab with LLHM = 20  cm at z = 0 and z = 20  cm, in the first row and the second row, respectively. Figure  3(b) shows the transverse field distribution of the BG beam with Rp = 5 in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. Figure  4(b) shows the transverse field distribution of the ELG beam with Rp = 10 in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. In these three cases beam diverges with propagating in Kerr LHM slab and focuses with propagating in free space after the slab.

Figure  2(c) shows the transverse field distribution of the EHChG beam with Rp = 1.15 in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. It can be seen that divergence and therefore self-focusing are reduced for the same incident beam power in thinner slabs.

Figure  3(c) shows the transverse field distribution of the BG beam with Rp = 2.5 in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. It can be seen that for the same slab thickness, reducing incident beam power causes less divergence of the beam in the slab and also less self-focusing when propagating in free space. Figure  4(c) shows the transverse field distribution of the BG beam with Rp = 10 in a slab with LLHM = 7  cm at z = 0 and z = 7  cm, in the first row and the second row, respectively. It can also be seen that divergence and therefore self-focusing are reduced for the same incident beam power in thinner slabs.

Figure  2(d) shows the transverse field distribution of the EHChG beam with Rp = 0.5 in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. Figure  3(d) shows the transverse field distribution of the BG beam with Rp = 0.5 in a slab with LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively. Figure  4(d) shows the transverse field distribution of the ELG beam with Rp = 0.5 in a slab with LLHM = 7  cm at z = 0 and z = 7  cm, in the first row and the second row, respectively. It can be seen from these three cases that even for Rp < 1 self-focusing happens, which is impossible for a conventional Kerr media.

The other case is χ < 0. In this case, the self-focusing happens in the Kerr LHM slab and then diverges in the next free space after it. Figure  2(e) shows the transverse field distribution of the EHChG beam with Rp = 1.15 in a slab LLHM = 10  cm at z = 0 and z = 10  cm, in the first row and the second row, respectively.

Figure  3(e) shows the transverse field of the BG beam with Rp = 10 in a slab with LLHM = 3  cm at z = 0 and z= 3  cm, in the first row and the second row, respectively. Figure  4(e) shows the ELG beam with Rp = 10 in a slab with LLHM = 7  cm at z = 0 and z = 7  cm, in the first row and the second row, respectively. Figure  2(f) shows the transverse field distribution of the EHChG beam with Rp = 2.3 in a slab with LLHM = 20  cm at z = 0 and z = 20  cm, in the first row and the second row, respectively. Figure  3(f) shows the intensity distribution of the BG beam with Rp = 10 in a slab with LLHM = 5  cm at z = 0 and z = 5  cm, in the first row and the second row, respectively. Figure  4(f) shows the field distribution of the ELG beam with Rp = 5 in a slab with LLHM = 7  cm at z = 0 and z = 7  cm, in the first row and the second row, respectively.

These three cases show that a lower incident beam power leads to less convergence inside the slab with the same thickness and also less divergence after propagating in free space.

4.3. Period length and focal length of LHM slabs

So far we have investigated the laser beam propagation in a certain slab thickness and after a distance as long as the slab in free space. Now we are going to consider longer media of Kerr LHM and next free space to find out the general behavior of laser beams in Kerr LHM media and the focal length of lens like Kerr LHM slabs. As mentioned before, for a Kerr LHM slab with negative nonlinearity, the beam focusing through the slab has a periodic behavior, which depends on the incident beam power.

Figure  5 shows the EHChG beam waist evaluation through the nonlinear Kerr media in the case of χ < 0 with LLHM = 100  cm, panel  (a) for Rp = 1.15 and panel  (b) for Rp = 2.3. As can be seen, incident beams with higher powers focus more in a shorter focusing period length.

Fig.  5. The EHChG beam waist evaluation through the Kerr LHM slab with LLHM = 100  cm, for (a) Rp = 1.15 and (b) Rp = 3.

The same argument is also true for BG beams. But in the case of Laguerre– Gaussian beams, after the first focusing point, the beam deforms very quickly; however, the deformed beams still have periodic behavior.

For a Kerr LHM media with positive nonlinearity, the beam diverges in the concerned media and the focusing happens in the free space after the slab, in fact the slab acts like a lens, as mentioned before. Figure  6 shows the EHChG beam waist evaluation in the free space after the Kerr “ left-handed” matamaterial slab, panels  (a) and (c) for Rp = 1.15; LLHM = 10  cm in the first row and LLHM = 15  cm in the second row; panels  (b) and (d) for LLHM = 20  cm; Rp = 1.15 in the first row and Rp = 2.3 in the second row. As can be seen, with an increase in the slab thickness and the incident power, the focal length locates at a near distance from the slab. In addition, increasing slab thickness leads to more self-focusing, as pointed out previously.

Fig.  6. The EHChG beam waist evaluation in the free space after the LHM slab, panels  (a) and (c) for Rp = 1.15; LLHM = 10  cm, in the first row, and for LLHM = 15  cm, in the second row; panel  (b) and (d) for LLHM = 20  cm; Rp = 1.15, in the first row, and for Rp = 2.3 in the second row.

4.4. A multilayer structure

A beam propagating in long enough Kerr LHM media will cause the beam to break down, and high incident beam power causes the beam to break down even more quickly. Therefore, a multilayer structure with subsequent RHM and LHM media layers is proposed to focus the incident beam. Figure  7 shows the schematic configuration of the considered multilayer structure. Every LHM slab is considered to be placed at the focal length of the previous LHM slab. Figure  8 shows the transverse field distribution of the EHChG beam for Rp = 2.3, ω 0 = 0.4  mm, LLHM = 5  cm, LRHM1 = 18  cm, LRHM2 = 12  cm, LRHM3 = 5  cm, at every interface of the structure, respectively. As expected, in every RHM the beam has got more focus. Therefore, self-focusing happens 50  cm after the incident beam.

Fig.  7. Schematic configuration of a multilayer structure.

Fig.  8. Intensity distribution of the EHChG beam with m = n = 2 in x = y = 0 plan, at every interface of structure that showed in Fig.  7. respectively, for Rp = 2.3, ω 0 = 0.4  mm, LLHM = 5  cm, LRHM1 = 18  cm, LRHM2 = 12  cm, LRHM3 = 5  cm.

5. Conclusion

The focusing properties of laser beams in a nonlinear LHM media involve two cases, positive nonlinearity and negative nonlinearity. In a Kerr LHM media with positive nonlinearity, the beams diverge in the slab and then focus when propagating in free space, which is called self-focusing. The focal length of the slab depends on incident beam power and slab thickness. The same behavior is observed in a linear LHM slab, but in this case the focused beam waist cannot be smaller than the incident beam waist; however, there is no such limitation for a Kerr LHM slab. In addition, the self-focusing can happen in a positive nonlinear LHM media for an incident beam power that is below the critical power which cannot happen in a conventional Kerr media. The other case is a Kerr LHM media with negative nonlinearity. In this case the beam focuses through the Kerr LHM media and then diverges in free space after the slab. Beam focusing in a Kerr LHM has a periodic pattern which depends on the incident beam power. In addition, in both positive and negative nonlinearity cases the focusing behavior of the beam can be controlled by changing the incident beam power and the thickness of the slab. In a multilayer structure with subsequent RHM and LHM layers, self-focusing can happen for lower incident beam powers.

It can be seen from simulations that EGChG, BG, and ELG beams have the same behavior in a Kerr LHM media, while beam deformation happens faster in the case of BG, ELG, and EGChG beams with the same incident power, respectively.

Reference
1 Veselago V G 1968 Soviet Physics Uspekhi 10 509 DOI:10.1070/PU1968v010n04ABEH003699 [Cited within:1]
2 Pendry J B 2000 Phys. Rev. Lett. 85 3966 DOI:10.1103/PhysRevLett.85.3966 [Cited within:1] [JCR: 7.943]
3 Shelby R A, Smith D R and S Schultz 2001 Science 292 77 DOI:10.1126/science.1058847 [Cited within:1]
4 Smith D R, Pendry J R and Wiltshier M C K 2004 Science 305 788 DOI:10.1126/science.1096796 [Cited within:1]
5 Guo B 2013 Chin. Phys. Lett. 30 105201 DOI:10.1088/0256-307X/30/10/105201 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
6 Ye Y H and Zhong M 2014 Chin. Phys. B 23 024101 DOI:10.1088/1674-1056/23/2/024101 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
7 Wang F M, Liu H, Li T, Dong Z G, Zhu S N and Zhang X 2007 Phys. Rev. E 75 016604 DOI:10.1103/PhysRevE.75.016604 [Cited within:1] [JCR: 2.313]
8 Ye Y H and Zhang J Y 2005 Opt. Lett. 30 1521 DOI:10.1364/OL.30.001521 [Cited within:1] [JCR: 3.385]
9 Ortuno R, Garcia-Meca C, Rodriguez-Fortuno F J, Marti J and Martinez A 2009 Phys. Rev. B 79 075425 DOI:10.1103/PhysRevB.79.075425 [Cited within:1]
10 Chen J B J, Grzegorczyk T M, Wu B I and Kong J A 2005 J. Appl. Phys. 98 094905 DOI:10.1063/1.2128698 [Cited within:1] [JCR: 0.71]
11 Ziolkowski R W and Kipple A D 2003 IEEE Trans. Anten. Progag. 51 2626 DOI:10.1109/TAP.2003.817561 [Cited within:1]
12 Ziolkowski R W and Erentok A 2006 IEEE Trans. Commun. 54 7 DOI:10.1109/TCOMM.2005.861682 [Cited within:1]
13 Schurig D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F and Smith D R 2006 Science. 314 977 DOI:10.1126/science.1133628 [Cited within:1]
14 Lu L, Qu za S B, Shi H Y, Zhang A X, Xia S, Xu Z and Zhang J Q Acta Phys. Sin. 63 028103 (in Chinese) DOI:10.7498/aps.63.0281032014 [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
15 Qin M M, Ji W, Feng Y Y and Feng W 2014 Chin. Phys. B 23 028103 DOI:10.1088/1674-1056/23/2/028103 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
16 Wang G D, Liu M H, Hu X W, Kong L H, Cheng L L and Chen Z Q 2014 Chin. Phys. B 23 017802 DOI:10.1088/1674-1056/23/1/017802 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
17 Lu L, Qu S B, Su X, Shang Y B, Zhang J Q and Bai P Acta Phys. Sin. 62 208103 (in Chinese) DOI:10.7498/aps.62.2081032013 [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
18 Xu R W, Guo L X and Fan T Q 2013 Chin. Phys. Lett. 30 124101 DOI:10.1088/0256-307X/30/12/124101 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
19 Zharova N A, Shadrivov I V, Zharov A A and Kivshar Y S 2005 Opt. Express 13 1291 DOI:10.1364/OPEX.13.001291 [Cited within:1] [JCR: 3.546]
20 Tian H, Liu H T and Cheng H F 2014 Chin. Phys. B 23 025201 DOI:10.1088/1674-1056/23/2/025201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
21 Zharov A A, Shadrivov I V and Kivshar Yu S 2003 Phys. Rev. Lett. 91 037401 DOI:10.1103/PhysRevLett.91.037401 [Cited within:1] [JCR: 7.943]
22 Lapine M, Gorkunov M and Ringhofer K H 2003 Phys. Rev. Lett. 67 065601 [Cited within:1] [JCR: 7.943]
23 Hu Y, Wen S, Zhuo H, You K and Fan D 2008 Opt. Express 16 7 DOI:10.1364/OE.16.000007 [Cited within:1] [JCR: 3.546]
24 Wen S, Xiang Y, Dai X, Tang Z, Su W and Fan D 2007 Phys. Rev. A 75 3 [Cited within:1] [JCR: 3.042]
25 Taha T R and Ablowitz M J 1984 J. Comput. Phys. 55 20330 [Cited within:1] [JCR: 2.138]
26 Tovar A A and Casperson L W 1998 J. Opt. Soc. Am. A 15 2425 DOI:10.1364/JOSAA.15.002425 [Cited within:1] [JCR: 1.665]
27 Saghafi S and Sheppard C J R 1998 J. Mod. Opt. 45 1999 DOI:10.1080/09500349808231738 [Cited within:1]
28 Gori F, Guattari G and Padovani C 1987 Opt. Commun. 64 491 DOI:10.1016/0030-4018(87)90276-8 [Cited within:1] [JCR: 1.438]