†Corresponding author. E-mail: yjxia_sd@126.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61178012 and No.11147019).
We investigate the protection of quantum correlations of two qubits in independent vacuum reservoirs by means of weak measurements. It is found that the weak measurement can reduce the amount of quantum correlation for one type of initial state at the beginning in a non-Markovian environment and meanwhile it can reduce the occurrence time of entanglement sudden death (ESD) in the process of time evolution. In a Markovian environment, the quantum entanglements of the two kinds of initial states decay rapidly and the weak measurement can further weaken the quantum entanglement, therefore in this case the entanglement cannot be optimized in the evolution process.
Quantum correlations, including quantum entanglement (QE) and quantum discord (QD), as the heart of quantum information, [1– 4] have been investigated in different conditions and environments since they were first put forward.[5– 24] These studies indicated that there is a possibility of a complete disappearance of QE within a finite time during the evolution of joint entanglement of a pair of qubits exposed to the local noise environments, [4, 15] which has been called entanglement sudden death (ESD) and has been proven to occur in a quantum optics experiment. The conception of QD comes from the fact that two classically identical expressions for the mutual information are generally different in a quantum system. The difference is defined as QD.[1, 7, 11, 16] All quantum correlations can be characterized by the QD instead of entanglement for pure entanglement states. For mixed states, the entanglement cannot totally describe the quantum correlation. Even for some separable states, although there is no entanglement between these two parts, the QD is nonzero, which indicates the presence of quantum correlations. The QD offers new prospects for quantum information processing. As for the fundamental aspects in quantum theory and the important application in quantum information processing of quantum correlations, the evolution of quantum correlation dynamics is widely studied in various conditions and environments, such as a closed system, an open system including Markovian and non-Markovian environment, a damped cavity, etc.[5– 23]
How to optimize the quantum correlation dynamics is the aim of this paper. Entanglement dynamics in open system have been already investigated by Bellomo et al., [6] which indicates that the phenomenon of ESD appeared in the evolution procession. Using weak measurement reversals to cope with the recovery of the initial state has been put forward recently.[24– 29] In this work, we investigate optimizing quantum correlations by weak measurement reversal in a Markovian and non-Markovian environment.
The rest of the present paper is organized as follows. In Section 2, we show a general procedure of the theoretical protocol to recover the region of ESD of quantum correlations in a two-qubit system and the effects of QD on the second thoughts. In Section 3, we mathematically analyze the initial state evolution compared with the quantum state after weak measurement operation. In Section 4, we draw some conclusions from the present study.
We introduce the damped Jaynes– Cummings model in Ref. [5] where a two-level atom is coupled to a single cavity mode, and then the cavity is coupled to a reservoir consisting of harmonic oscillators in the vacuum state. An excited two-level atom interacts with the vacuum field at zero temperature. The whole system keeps to Schrö dinger’ s equation. The effective spectral density of reservoir can be described as an electromagnetic field of dissipative cavity, which is,
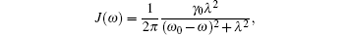
where λ is the spectral width of the coupling and γ 0 means the dissipative rate. The probability amplitude is given by

Here, 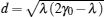
In order to investigate the evolution of two entangled two-level atoms, we make each atom locally interact with two independent reservoirs, respectively. According to the techniques of Kraus, [6] we can obtain the elements of the reduced density matrix as follows:

We adopt the weak measurement to analyze the effect on the evolution of entangled atoms. The map of weak measurement describing a two-level atom interacting with a vacuum environment at zero temperature is as follows:[27– 29]

Here, p corresponds to the finite success probability for the weak measurement, it can also be called weak measurement intensity.
Now, we use the above theories to deal with a two-qubit system, whose initial state is Bell’ s type φ (0) = α | 00〉 + β | 11〉 and ϕ (0) = α | 01〉 + β | 10〉 , where | α | 2 + | β | 2 = 1. At the beginning we make each qubit evolve in an independent dissipative cavity. According to Eq. (3), after weak measurement the quantum state can be written as
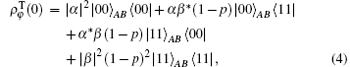
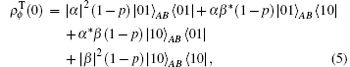
where 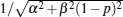

For the entanglement state whose initial matrix has X structure, [16] its reduced matrix is
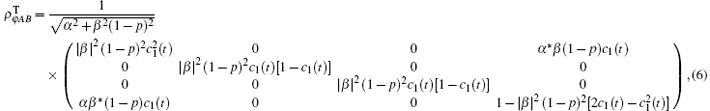
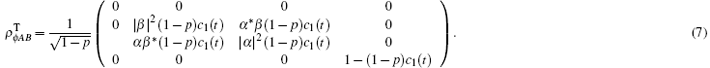
Its concurrence[6] should be written as the following expression 

By calculation we can obtain
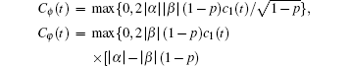

Combining initial condition and Eq. (9), we may obtain the evolution characteristics of entangled qubits.
According to the following equation we can also analyze the QD:[7, 30]

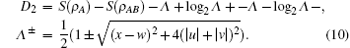
We take the relation between spectral width of the coupling and dissipative rate as λ = 0.1γ 0 conveniently. By making use of Eqs. (9) and (10) we investigate the evolution characteristics of the two-qubit system in a reservoir.
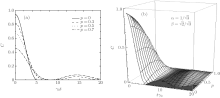
As shown in Figs. 1 and 2, the phenomenon of entanglement sudden death happens in the dynamic evolution process of the two-qubit system in the non-Markovian reservoir environment. The region of ESD is dependent on the value of amplitude | α | 2. With the value of | α | 2 increasing, the time of ESD is shorter and shorter as indicated in Fig. 1(a). It can also reduce the time of ESD by weak measurement when the value of | α | 2 is unchangeable (Figs. 2(a) and 2(b)). In addition, the weak measurement can optimize ESD in different values of | α | 2 and the optimization effect becomes more apparent by increasing the weak measurement intensity, as shown in Figs. 1(a)– 1(d). But another consequence brought by weak measurement is to reduce the initial evolution of quantum entanglement. From the above discussion we can obtain that the weak measurement operation can reduce or avoid the happening of ESD, and can improve the intensity of quantum entanglement in the process of dynamic evolution.
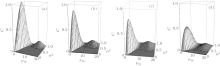 | Fig. 1. Revivals of entanglement sudden death by weak measurement in non-Markovian environment: (a) p = 0, (b) p = 0.3, (c) p = 0.5, and (d) p = 0.7. |
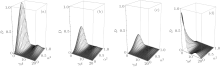
The evolution of quantum discord in non-Markovian environment is shown in Fig. 3. We can find that weak measurement reduces the intensity of quantum discord in the evolution process. With the increasing strength of weak measurement, quantum discord decays faster in the evolution process, as shown in Figs. 3(a)– 3(d). Obviously, the weak measurement accelerates the decay of quantum discord, leading to us being unable to realize optimization in the process of quantum discord evolution.
There is no ESD happening in the evolution process of the initial state ϕ (0) = α | 01〉 + β | 10〉 in a non-Markovian reservoir (Fig. 4(a)). The operation of weak measurement can reduce the intensity of quantum entanglement in the process of evolution (Figs. 4(b) and 4(c)). Taking maximum entanglement for example (Fig. 4(d)), we find that the entanglement between quantum qubits decreases immediately in the evolution process with the increasing weak measurement intensity. Therefore, we can draw a conclusion that a weak measurement cannot optimize the evolution of quantum entanglement for the initial state ϕ (0) = α | 01〉 + β | 10〉 .
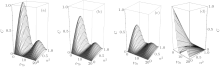 | Fig. 4. Effects of weak measurement on quantum entanglement in non-Markovian environment: (a) p = 0, (b) p = 0.3, (c) p = 0.5, and (d) 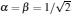 |
 | Fig. 5. Evolutions of quantum discord in non-Markovian environment by weak measurement operation: (a) 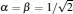  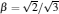 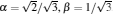 |
In addition, the weak measurement operation can also reduce the intensity of quantum discord in the evolution process for initial state ϕ (0) = α | 01〉 + β | 10〉 even it is initially in a maximum entanglement state (Fig. 5(a)), and on account of the basis vector’ s symmetry of ϕ (0) = α | 01〉 + β | 10〉 , the evolution of the state presents a symmetric distribution (Figs. 5(b) and 5(c)). That is to say, the weak measurement cannot optimize the evolution of quantum discord for the initial state ϕ (0) = α | 01〉 + β | 10〉 .
In this section we investigate only the effect for quantum entanglement by weak measurement, by taking the relation between spectral width of the coupling and dissipative rate as λ = 3γ 0 conveniently.
The quantum entanglement decreases immediately during the evolution of the initial states φ (0) = α | 01〉 + β | 11〉 and ϕ (0) = α | 01〉 + β | 10〉 in the Markovian environment. The weak measurement can revive the ESD for the state φ (0) = α | 00〉 + β | 11〉 (Fig. 6), which reveals the same rule as that in the non-Markovian environment (Figs. 6(a) and 6(b)).
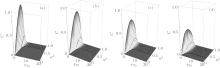 | Fig. 6. Revivals of entanglement sudden death by weak measurement in Markovian environment: (a) p = 0, (b) p = 0.3, (c) p = 0.5, and (d) p = 0.7. |
The entanglement evolution of the other Bell’ s type initial state ϕ (0) = α | 01〉 + β | 10〉 also decreases rapidly in the Markovian environment. The phenomenon becomes more apparent with the increasing weak measurement intensity (Figs. 7(a)– 7(c)).
 | Fig. 7. Effects of weak measurement for quantum entanglement in Markovian environment: (a) p = 0, (b) p = 0.3, (c) p = 0.5, and (d)  |
From the above investigation, we find that the weak measurement can optimize the ESD but cannot improve the quantum entanglement intensity in the evolution process in a Markovian environment.
Utilizing the weak measurement technique, we investigate the dynamic evolution of quantum correlations (including QE and QD) in two different Bell’ s type quantum pure state systems. In the non-Markovian environment, the weak measurement operation can reduce or avoid the happening of ESD, and can improve the intensity of quantum entanglement in the process of dynamic evolution. It can also accelerate the decay of quantum discord but is unable to realize the optimization in the process of quantum discord evolution. In the Markovian environment, the weak measurement can optimize the ESD but cannot improve the quantum entanglement intensity in the evolution process.
By mathematical analysis and comparison, we make a conclusion that the weak measurement techniques can improve the quantum entanglement intensity and reduce the entanglement sudden death time in a non-Markovian reservoir, but can only optimize entanglement sudden death time and cannot improve the entanglement intensity in the Markovian environment.
We thank Drs. Man Z X and Zhang Y J for helpful discussion.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|