Coherent population trapping (CPT), ^{[1, 2]} which refers to the phenomenon of an atom population being trapped in a dark state (a superposition state of the lower levels) and the optical field propagating through it without absorption, is currently attracting considerable interest in quantum optics and atomic physics. The CPT effects may not only become a significant demonstration of quantum coherence and interference, but may also have potential applications in laser cooling, ^[3] atomic magnetometer, ^{[4, 5]} squeezing and entanglement, ^[6] and atomic clock.^{[7, 8]} Therefore, a great deal of theoretical and experimental work has been focused on the CPT effects in various systems.^{[1, 2, 9– 14]} For example, the atomic system has been an important system for realizing CPT phenomenon via different methods.^{[1, 2, 9– 11]} It is found that semiconductor quantum wells and quantum dot could be used to generate the population trapping.^{[12, 13]} Recent research shows that the maximal atomic coherence can be also obtainable in a diamond under optical excitation.^[14]

It is well known that driving-field manipulations have been shown to be an effective and significant way to provide quantum coherence and interference effects.^{[15– 31]} It is particularly important that the phase modulations of the applied fields play a crucial role in the coherent optical phenomena.^{[22– 31]} The phase-dependent electromagnetically induced transparency (EIT) and CPT have been investigated in a coherent-driving atomic system.^{[22– 25]} The atomic spontaneous emission can be effectively suppressed via the laser phases.^[26] The atom localizations could be implemented via the phase control of the applied fields.^[27] The phase control of subluminal and superluminal propagation of light has been investigated in the driven multilevel atomic systems.^{[28, 29]} It is also shown that the laser-field phase could be applied to manipulate quantum entanglement^[30] and the refractive index.^[31] We note that many phase-dependent optical phenomena have been limited to the atomic system.

On the other hand, superconducting quantum circuits have recently been applied to demonstrate many quantum optical effects and practical applications in information processing.^{[32– 42]} Some striking features and advantages are included in such a system. First, the superconducting circuit system could be artificially structured with flexible designs and be easily controlled for the experimental parameters, which are absent in the atomic system. Second, the passing microwave field which is coupled with the superconducting qubit could be only transmitted or reflected. But in the atom– light interaction system, the optical field in three dimensions undergoes scattering, absorption, and dispersion, which leads to high noise and is harmful for the information processing. Last, but not least, just a single artificial atom is involved in the superconducting circuit system, whereas there are usually many atoms in the atom– laser coupling system. It is worth mentioning that many interesting optical phenomena have been demonstrated in such a device. Resonance fluorescence has been observed in a two-level artificial atom in an open transmission line.^[35] CPT and EIT phenomena have been demonstrated in a single macroscopic superconducting quantum system.^{[36– 38]} The Autler– Townes effect has been measured in a driven superconducting three-level system.^[39] Some typical nonlinear optical phenomena have also been shown in the superconducting qubit, such as light storage, ^[40] Kerr nonlinear effect, ^[41] optical mixing, ^[42] and so on.

In this paper, we study the phase-dependent CPT effect in a single driven three-level Δ -type artificial atom consisting of a superconducting fluxonium qubit. When three external fields are applied to different atomic transitions of such a qubit, the optical properties of the system depend strongly on the relative phase and intensities of the external fields. It is shown that the maximal atomic coherence is present and CPT is obtained when the relative phase is taken as 0 or π . To the contrary, for the π /2 relative phase, the quantum coherence decreases and a small amount of population is transferred to the upper level. On the other hand, for the fixed π /2 relative phase, the modulus of the off-diagonal density matrix element with regard to two lower levels, which determines the quantum coherence, is controlled by the intensity of the field applied to the lowest atomic transition. When the intensity is strong, the modulus of the off-diagonal density matrix element becomes reducing and it can increase for weak intensity. The root of these phenomena is due to quantum interference. For the case of the 0(π ) relative phase, destructive interference occurs and coherently prepared atoms are decoupled from the microwave field applied to two lower levels. But for the π /2 relative phase, the instructive interference is dominant and the CPT effect is not satisfied. We provide an alternative superconducting system to show the phase-dependent CPT phenomenon, which is useful for the optical communication and nonlinear optics in solid-state devices.

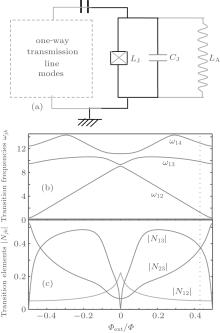
We first consider a single superconducting fluxoninum qubit (shown in Fig.  1(a)), which consists of a small Josephson junction and a large Josephson junction array, and we could write its Hamiltonian as^{[43– 45]}

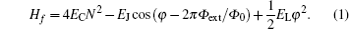
Here the operator N = Q/(2e) denotes the reduced charge on the junction capacitance across the small junction (in units of Cooper-pair charge 2e). The operator φ = 2π Φ /Φ ₀ (Φ ₀ = h/(2e) being the flux quantum) describes the loop flux in such units that φ coincides with the phase difference across the small junction, and the parameter Φ _ext is the external magnetic flux. The coefficients E_C = e²/(2C_J), and E_J = (Φ ₀/2π )²/L_J, respectively, represent the charging energy and the Josephson energy of the small junction, and the parameter E_L = (Φ ₀/2π )²/L_A is effective inductive energy of the Josephson junction array. In order to obtain the eigenvalues and eigenstates of the fluxonium Hamiltonian, we employ the three-step operations as shown in Ref.  [45]. (i) We choose φ as the generalized coordinate and N as the generalized momentum, which satisfy the operator commutation relation [φ , N] = i, and thus we have the form N = − id/dφ in φ representation, which is analogous to the usual position– momentum commutation relation. (ii) We consider the case of E_J = 0 and the harmonic-oscillator-like model is present. Thus we could use the harmonic oscillator basis {| n〉 } and write H_{f| EJ} = 0 = ħ ω _p(a^† a + 1/2) with a^† and a being the usual creating and annihilation operators and 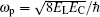being the oscillator frequency. (iii) In the new basis, the fluxonium Hamiltonian can be expressed as H_f = ∑ _{n, n′} H_nn′ | n〉 〈 n′ | and the Hamiltonian matrix element H_nn′ has the form as H_nn′ = ħ ω _p(n + 1/2)δ _nn′ − E_J cos(2π Φ _ext/Φ ₀) 〈 n| cosφ | n′ 〉 − E_J sin(2π Φ _ext/Φ ₀) 〈 n| sinφ | n′ 〉 . It is noted that the matrix elements 〈 n| cosφ | n′ 〉 and 〈 n| sinφ | n′ 〉 have very complicated formulas and they are not shown here to save space. After doing the above operations, we obtain the numerical diagonalization Hamiltonian with H_f = ∑ _lħ ω _l| l〉 〈 l| and the spectroscopy frequencies ω _l. For the present system, the amplitudes of photon-induced transitions between different energy levels are then determined by the charge matrix elements N_jk = 〈 j| N| k〉 with j and k being the eigenstates. In particular, the energy transition frequencies and the charge matrix elements as a function of the flux bias Φ _ext/Φ ₀ are shown in Figs.  1(b) and 1(c), where the parameters are from the experimental data in Ref.  [43].

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. (a) A fluxonium circuit model, consisting of a small Josephson junction and a large Josephson junction array, is capacitively coupled to a transmission line. (b) For the fluxonium qubit, the transition frequencies of the lowest eigenstates, and (c) the charge matrix elements as a function of the flux bias Φ ext/Φ , where the parameters are from the experiments with EC = 2.5  GHz, EL = 0.52  GHz, EJ = 9.0  GHz. Here we focus on the case of Φ ext/Φ = 0.43, indicated by the dotted vertical line, where the condition | N13| = | N23| is obtained.

For the sake of studying the CPT effects, here we focus on the lowest three energy levels of the fluxonium qubit. It is obvious from Fig.  1(c) that all three matrix elements have comparable values when the flux bias is away from 0 and ± 0.5, and thus the Δ -type three-level structure is generated, which is absent in the natural atom system. Here we use the interactions of such a system with external applied electromagnetic field to obtain the phase-dependent CPT effect. For the three-level fluxonium, the level states are denoted by | 1〉 , | 2〉 , and | 3〉 and three electromagnetic fields are applied to couple with the different transitions of the qubit, which can be performed by connecting the fluxonium to a transmission-line traveling modes, as shown Fig.  1(a). In the rotating wave approximation, the total Hamiltonian is expressed as (ħ = 1)

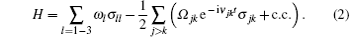
Here the operators σ _jk = | j〉 〈 k| are population operators for j = k and are atomic flip operators for j ≠ k. The coefficients Ω _jk (j, k = 1 ∼ 3, j ≠ k) are complex Rabi frequencies of the corresponding external fields with the frequencies ν _jk and are given by Ω _jk = gN_jk, where the parameter g is electric-dipole coupling frequency. Based on the unitary operator U = exp(− iν ₃₁tσ ₁₁ − iν ₃₂tσ ₂₂) with a choice of zero-point energy ω ₃ = 0 and transformed the new rotating frame, the total Hamiltonian of the system becomes

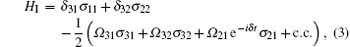
where δ _jk = ν _jk − ω _jk, δ = δ ₃₂ + δ ₂₁ − δ ₃₁ with ω _jk = ω _j − ω _k. Meanwhile, the quantum relaxation of such a system can be described by a density master equation

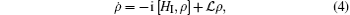
where 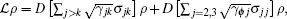and D[A] • : = A • A^† − {A^† A, • }/2. The parameters γ _jk are the decay rates of a qubit, which are originated from the spontaneous emission into the dissipative bath associated with the qubit circuit and into the measurement apparatus.^[44] And γ _{ϕ j} are the dephasing rates for the levels | j〉 , which are due to the quantum noises from the fluctuations of the energy parameters E_J, E_L, and the external magnetic flux Φ _ext.^[44] We note that the three-level Δ -type fluxonium qubit has negligible dephasing relaxations at certain conditions.^{[38, 43]}

In terms of the density master equation and the total Hamiltonian, the density matrix elements are easily derived by

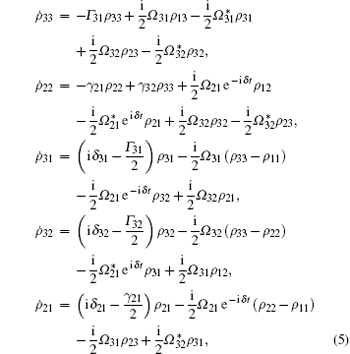
together with 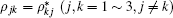and ρ ₁₁ + ρ ₂₂ + ρ ₃₃ = 1, where the parameters are given by Γ ₃₁ = γ ₃₁ + γ ₃₂ and Γ ₃₂ = γ ₃₁ + γ ₃₂ + γ ₂₁.

In order to show the influences of the applied-field phases on the quantum optical phenomena, we take a two-step transformation, as follows. Firstly, we express the complex Rabi frequencies as Ω _jk = | Ω _jk| e^{− iϕ _jk}, where | Ω _jk| are real Rabi frequencies of the corresponding applied fields and ϕ _jk are their initial phases. Secondly, we make transformations for density matrix elements, such as ρ _jj = ρ ̃ _jj, ρ ₃₁ = ρ ̃ ₃₁e^{− iϕ ₃₁}, ρ ̃ ₃₂ = ρ ̃ ₃₂e^{− iϕ ₃₂}, ρ ₂₁ = ρ ̃ ₂₁e^{− i(ϕ ₃₁− ϕ ₃₂}). After the above two-step operations we finally have

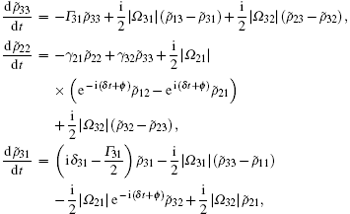
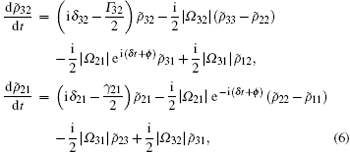
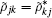
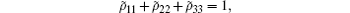
constrained by and

where the parameter ϕ = ϕ ₃₂ + ϕ ₂₁ − ϕ ₃₁ is the relative phase of three applied fields. We note that there are time terms in Eq.  (6). For δ = 0, i.e., the three-photon resonance is satisfied, the stationary solutions for the density matrix elements are easily obtained via setting the time derivative in Eq.  (6) to be equal to zero. Under the condition of δ ≠ 0, the atomic behavior obviously depends on time and the case becomes quite complicated. For the sake of simplicity, we focus on our discussion for the three-photon resonance case (δ = 0), i.e., δ ₃₁ = δ ₃₂ + δ ₂₁, where the relative phase and intensities of the applied fields have huge effects on the steady-state density matrix elements and hence we will discuss the phase-dependent population trapping in the following.

We now discuss the steady-state coherence effects in a single strong-driven superconducting fluxonium qubit. For the sake of simplicity, we scale the Rabi frequencies | Ω _jk| and detunings δ _jk in the unit of γ ₃₁.

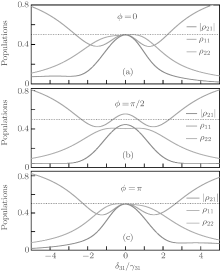
In Fig.  2 we present the numerical results by plotting the steady-state populations | ρ ₂₁| , ρ ₁₁, ρ ₂₂, which are dependent on the probe detuning and the relative phase of the applied fields. The parameters in the figure are chosen as follows: γ ₃₂ = γ ₃₁, γ ₂₁ = 0.01γ ₃₁, δ ₃₂ = 0, | Ω ₃₂| = | Ω ₃₁| = 2.5γ ₃₁, | Ω ₂₁| = 0.5γ ₃₁, ϕ = 0 (a), ϕ = π /2 (b), and ϕ = π (c). It is clearly seen that the value of coherence | ρ ₂₁| depends strongly on the relative phase. When the relative phase is tuned to ϕ = 0 or π , as shown in Figs.  2(a) and 2(c), the maximal coherence with | ρ ₂₁| = 0.5 can be obtained at the region of δ ₃₁ = 0, which means that the CPT phenomenon appears and the levels | 1〉 and | 2〉 are half/half populated. While for the case of ϕ = π /2, the value of | ρ ₂₁| decreases and a few population are transferred from the dark state to the upper level | 3〉 with the help of the external fields. It is noted that the coherence | ρ ₂₁| and populations ρ ₁₁, ρ ₂₂ are independent of the respective phases ϕ ₃₂, ϕ ₂₁, ϕ ₃₁, once the relative phase ϕ is fixed. When the relative phase ϕ remains unchanged, the values of | ρ ₂₁| , ρ ₁₁, ρ ₂₂ also remain unchanged no matter how the respective phases change, and thus the figure with respect to the respective phases is not shown here.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The steady-state populations | ρ 21| , ρ 11, ρ 22 versus the probe detuning δ 31/γ 31. The parameters are chosen as γ 32 = γ 31, γ 21 = 0.01γ 31, δ 32 = 0, | Ω 32| = | Ω 31| = 2.5γ 31, | Ω 21| = 0.5γ 31, ϕ = 0 (a), ϕ = π /2 (b), and ϕ = π (c).

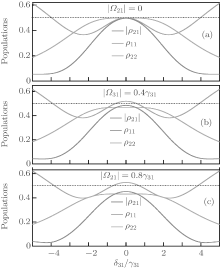
On the other hand, the CPT phenomenon is similarly sensitive to the intensities of the external fields. In order to observe the dependence, we fix the relative phase and adjust the Rabi frequency of the external field applied to two lower levels. As shown in Fig.  3, we plot the populations | ρ ₂₁| , ρ ₁₁, ρ ₂₂ as a function of the probe detuning δ ₃₁/γ ₃₁, where the parameters are given by γ ₃₂ = γ ₃₁, γ ₂₁ = 0.01γ ₃₁, δ 32 = 0, | Ω ₃₂| = | Ω ₃₁| = 4γ ₃₁, ϕ = π /2, | Ω ₂₁| = 0 (a), | Ω ₂₁| = 0.4γ ₃₁ (b), and | Ω ₂₁| = 0.8γ ₃₁ (c). When the field is absent from the transition between two lower levels, it is obvious that the maximal quantum coherence appears and the CPT phenomenon occurs due to the perfect destructive interference. When the external field is present and its intensity (| Ω ₂₁| ) rises, the value of coherence | ρ ₂₁| decreases at the zero-detuning region and the CPT effect is not satisfied because the instructive interference is dominant. The microwave fields excite the artificial atom to the upper state and simultaneously the atom absorbs the photons. In other words, the maximal quantum coherence and dark state are modified by the relative phase and intensities of the applied fields and the phase-dependent CPT effect could be obtainable, which may provide an effective approach to implement the photon switching.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The steady-state populations | ρ 21| , ρ 11, ρ 22 as a function of the probe detuning δ 31/γ 31, where the parameters are given by γ 32 = γ 31, γ 21 = 0.01γ 31, δ 32 = 0, | Ω 32| = | Ω 31| = 4γ 31, ϕ = π /2, | Ω 21| = 0 (a), | Ω 21| = 0.4γ 31 (b), and | Ω 21| = 0.8γ 31 (c).

The above phenomena could be made more clear in terms of the dressed-state method. In order to do so, we first implement the following three steps.

(i) We make first a transformation of the Hamiltonian H_I in Eq.  (3) by setting Ω _jk = | Ω _jk| e^{− iϕ _jk}, and | 1〉 = e^{− iϕ ₃₁}| 1̃ 〉 , | 2〉 = e^{− iϕ ₃₂} | 2̃ 〉 .

(ii) We then introduce a pair of new bases and express them as

(iii) For simplicity we assume the zero-detuning conditions δ ₃₁ = δ ₃₂ = δ ₂₁ = 0 and identical Rabi frequencies | Ω ₃₁| = | Ω ₃₂| . After the above operations we have

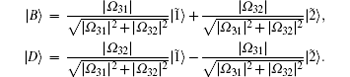
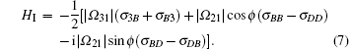
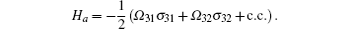
We now focus on analyzing the phase-dependent CPT phenomena via using the above dressed-state method.

Case 1 the relative phase being ϕ = 0 or π . In terms of Eq.  (7), we have

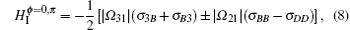
where the “ + ” sign corresponds to 0 relative phase and the “ − ” sign corresponds to π relative phase. Obviously, the field applied to two lower levels only leads to the level shifts of the states | B〉 , | D〉 and are not involved in driving and exciting the artificial atom. This means that the dark state | D〉 is still decoupled from the field. As a result, the atom remains the dark state | D〉 with the help of two driving fields | Ω ₃₁| , | Ω ₃₂| and decay channels. Meanwhile, no population is excited to the upper state | 3〉 . The maximal quantum coherence is obtainable and the CPT effect appears.

Case 2 the ϕ = π /2 relative phase. At this moment, the conditions cosϕ = 0 and sinϕ = 1 are satisfied and the Hamiltonian H_I is rewritten as

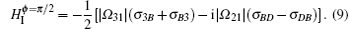
It is obvious that the states | B〉 , | D〉 are involved in interacting with the external fields. Similarly, we introduce a new pair of orthogonal states:

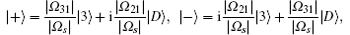
and rewrite the Hamiltonian as

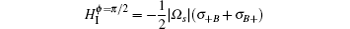
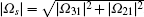
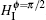
with . It is seen that the state | − 〉 is decoupled from the external field and it is one of eigenstates with respect to the Hamiltonian . Under the condition of joint population transfer via the driving fields (| Ω ₃₁| , | Ω ₂₁| ) and the decay channels, the atomic population is thoroughly trapped in the state | − 〉 , which is a superposition state consisting of the states | 3〉 and | D〉 . Therefore, a small amount of population is pumped into the upper state | 3〉 with the help of the small Rabi frequency | Ω ₂₁| and thus the coherence | ρ ₂₁| decreases.

We now discuss the feasibility of the scheme in the current experiments. Here we focus on the fluxonium qubit as proposed by the recent experiments.^{[43, 44]} It is well known that the Δ -type three-level structure can be easily realized via tuning the flux bias Φ _ext/Φ ₀, as shown in Fig.  1(c). In order to explicitly observe the phase dependence of the maximal quantum coherence, we choose the case of the flux bias Φ _ext/Φ ₀ = 0.43 slightly apart from 0.5, and the corresponding experimental parameters are estimated via the charge matrix elements shown in Fig.  1(c). Considering the condition of the Δ -type three-level artificial system coupled to the transmission-line traveling modes and using the results proposed in Refs.  [37], [38], and [44], we estimated the decay rates as γ ₃₁ = γ ₃₂ = 27.85  MHz, γ ₂₁ = 0.48  MHz, and the maximal Rabi frequency parameter | Ω | ≈ 110  MHz, which is available in experiment.^[39] Therefore, the phase-dependent coherent phenomena would be observed in the present system.

In conclusion, the CPT effect has been investigated in the three-level Δ -type superconducting fluxonium qubit driven by three electromagnetic fields applied to the different atomic transitions. The results show that the relative phase and intensities of the classical fields have huge effects on the maximal quantum coherence. When the relative phase is taken as 0 or π , the CPT phenomenon occurs and the maximal quantum coherence is obtainable. For the π /2 relative phase, however, the quantum coherence decreases with the few population being in the upper level. Furthermore, for the fixed π /2 relative phase, the value of coherence | ρ ₂₁| would become decreasing as the increase of the intensity for the field applied to the lowest atomic transition. The responsible mechanism is quantum interference. For ϕ = 0 or π , the destructive interference occurs and the field applied to two lower levels only leads to the level shifts of the bright state | B〉 and dark state | D〉 . Thus the dark state | D〉 is still decoupled from the field and the atom is trapped in such a state. The maximal quantum coherence is obtainable and the CPT effect appears. However, when ϕ = π /2, the dark state | D〉 is involved in interacting with the field and the quantum instructive interference is dominant. Therefore, a small amount of population is pumped into the upper state | 3〉 with the help of the small Rabi frequency | Ω ₂₁| . Our scheme utilizes the superconducting qubit, which is a feasible system for quantum state manipulation and quantum information processing in the future.