Recently, much work has been done to investigate the properties of beams carrying phase vortices.^{[1– 9]} Such beams carry orbital angular momentum and can impart this angular momentum to microscopic particles. Consequently, vortex beams have been studied for use as optical spanners and tweezers.^{[10, 11]} Another important feature of a vortex beam is that the topological charge of the vortex phase is a discrete variable and is stable under phase perturbation. This suggests that the phase topological charge could be utilized as an information carrier in free-space optical communications. However, for free-space optical communications, the laser beam should propagate through a turbulent atmosphere to transmit information to the receiver. The atmospheric turbulence may reduce the coherence of the source beam and then restrict the performance of these communication systems. Paterson’ s^[12] result shows that the decoherence effect of atmospheric turbulence on a communication system is important, even for weak turbulence. Greg and Robert’ s research also show that the topological charge of vortex beam is a robust quantity that can be used as an information carrier in optical communications. But the loss of topological charge may occur more rapidly in stronger turbulence.^[13] So the propagation properties of a vortex beam in atmospheric turbulence are very important for the system design and application performance estimation. In recent years, a great deal of attention has been paid to the properties of vortex beams in the atmosphere.^{[13– 23]} It has been demonstrated that atmospheric turbulence has a great influence on the topological charge, polarization, and intensity distribution of a vortex beam.

A Gaussian vortex beam is a kind of vortex beam that is easy to generate in a laboratory and in a real application system. The optical field of a Gaussian vortex beam can be described by adding a vortex phase to the TEM₀₀ Gaussian beam and the eye of the vortex is located at the beam optical axis. However, the short-term intensity pattern and the wander of the beam centroid of this vortex beam have not be studied so far. There has been no quantificational analysis about how the intensity hole varies as the turbulence strength and topological charge change. In this paper, the beam spreading and wandering properties of Gaussian vortex beams are investigated quantitatively by using numerical simulation. The intensity distribution and the dependence of energy hole diameter on the topological charge are discussed. How the topological charge affects the wandering of the beam centroid is analyzed for the first time.

According to the definition of the Gaussian vortex beam, the initial optical field of a Gaussian vortex beam could be described as

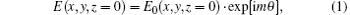
where E₀(x, y, z = 0) is the optical field of a Gaussian beam field of TEM₀₀, m is the topological charge of vortex phase, and θ is the angular coordinate of the point (x, y). For the collimated Gaussian vortex beam, E₀ can be expressed as

where A is a constant parameter that is determined by the optical source power and W₀ is initial beam radius.

The optical intensity distribution of a Gaussian vortex beam is the same as that of a Gaussian beam without vortex phase. The phase of a collimated Gaussian vortex beam has a helix distribution. Figure 1 shows the initial phase distributions of collimated Gaussian vortex beams with different topological charges.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Initial phase distributions of collimated Gaussian vortex beams with different topological charges: m = 1 (a), 2 (b), and 3 (c).

The numerical simulation of Gaussian vortex beam propagating in atmospheric turbulence is based on the Maxwell wave equation. According to the parabolic approximation of laser beam propagation, the optical filed of laser beam propagation in turbulence satisfies

where k = 2π /λ is the wave number, λ is the wavelength, n₁ = n − 1 is the variation of the index of refraction, with n being the refractive index of atmosphere. The multi-phase screen and Fourier transform method^[24] is widely used to solve Eq. (1) and to realize the dynamic propagation of an optical wave beam. The extended turbulent random atmosphere is divided into N_s slabs each with a thickness of Δ z. For a homogeneous atmospheric path, the medium may be modeled by identical spaced phase screens. So the distance between two phase screens is Δ z = L/N_s . The phase variation due to the turbulence of each phase screen is and the phase spectrum Φ _S can be described by

where Φ _n is the spectrum of the refractive index of the atmosphere, and κ _x and κ _y are the wavenumbers. For a Kolmogorov turbulence, with The optical field at position z_i can then be calculated by using

where F and F^{− 1} are the Fourier transform and the inverse Fourier transform, respectively.

After obtaining the final optical filed E(x, y, z = L) on the objective plane, the beam properties can be analyzed statistically, such as the spreading of the beam radius, the wandering of the beam centroid, and the intensity distribution structure. The parameters of the beam wave and numerical simulation are chosen to be λ = 1 μ m, W₀ = 60 mm, L = 1 km, Δ x = 1 mm, N = 256, where L is the propagation distance, Δ x is the grid interval, and N × N is the grid number in the simulation phase screen. In this paper, the propagation paths involved are all homogeneous paths, and the turbulent spectrum is assumed to be Kolmogorov spectrum.

Set the values of the structure constant of the refractive index of a homogeneous path to be 5 × 10^{− 16} m^{− 2/3}, 1 × 10^{− 14} m^{− 2/3}, 5 × 10^{− 14} m^{− 2/3}, and 1 × 10^{− 13} m^{− 2/3}, respectively, the values of Rytov index are 0.017, 0.332, 1.658, and 3.315, respectively, and choose the topological charge to be m = 1. The Rytov index is an integral parameter of and propagation distance L. As to a plane wave, is defined as , and for a homogeneous propagation path , where is always introduced to define the fluctuation condition of atmospheric turbulence: indicates a strong turbulence, indicates a weak turbulence, and indicates a critical turbulence condition.

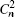
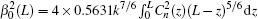
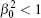
Figure 2 displays the corresponding short-term intensity patterns with different 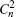. It can be seen that there is an intensity hole in the beam center in the presence of a vortex phase. (In the absence of the vortex phase the intensity pattern tends to be a Gaussian distribution, approximately.) In a weak turbulence, the intensity hole can be seen clearly. But as turbulence strength becomes stronger, the margin of the intensity hole becomes blurry and the disturbance of atmospheric turbulence gradually fills that hole. In Fig. 2(d), the intensity pattern breaks up and the intensity hole almost disappears.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Short-term intensity patterns with different turbulence strengths: (a), 0.332 (b), 1.658 (c), and 3.315 (d).

The filling effect can be seen more clearly in the long-term intensity patterns. Figure 3 shows the corresponding long-term intensity patterns, which are averaged over 500 short-term intensity patterns.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Long-term intensity patterns with different turbulence strength: 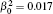(a), 0.332 (b), 1.658 (c), and 3.315 (d).

The size of the intensity hole and its variation in the atmosphere are important for analyzing the effect of the vortex phase on the vortex beam propagation. We calculate the energy contained in a specific disk with radius r, namely bucket energy, which is shown in Fig. 4. The energy is normalized to the power of the beam source, so we call it relative bucket energy. The long-term patterns involved in Fig. 4(b) are averaged over 1000 short-term intensity patterns. It can be seen that there is almost no energy for r < 4 mm when . And as the turbulence strength turns stronger, the intensity hole is gradually filled by energy. However, the relative bucket energy is also less than 2.5%, even in a strong turbulence for r < 10 mm.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Relative bucket energies in a disk versus disk radius and turbulence strength: short-term and (b) long-term.

We calculate the relative bucket energy P_{10 mm} in a disk for radius r = 10 mm as a function of Rytov index with topological charges: m = 0, m = 1, and m = 2, respectively, which is shown in Fig. 5. We can see that for a Gaussian beam with no vortex phase (m = 0) the relative bucket energy tends to decline as turbulence turns stronger, which happens because of the beam spreading due to atmospheric turbulent effects. For Gaussian vortex beams (m = 1 and m = 2) the relative bucket energy increases from a very small value to the peak value as the turbulence turns from weak to strong. This indicates that atmospheric turbulence has the effect or ability to fill the intensity hole. It can also be seen that for larger topological charge the relative bucket energy P_{10 mm} may be smaller. When the relative energies are 4.2%, 2.5%, and 1.4% for m = 0, 1, 2, respectively.

Fig. 5.

	Figure Option ViewDownloadNew Window
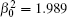
	Fig. 5. Plots of relative bucket energy P10 mm versus turbulence strength with different topological charges.

We assume the radius R_5% which contains 5% of the total energy to be the radius of the intensity hole of a vortex beam propagating in the atmosphere. Figure 6 shows plots of the R_5% of long-term intensity patterns versus turbulence strength with topological charges m = 1 and m = 2. It can be seen that R_5% = 17.0 mm and R_5% = 22.8 mm, respectively, for m = 1 and m = 2 when there is no atmospheric turbulence. These two radii are very large, which contain only 5% of the total energy, indicating that the intensity– hole effect of vortex beam is very serious when propagating in a vacuum. However, R_5% declines quickly as the turbulence becomes strong. This happens because the disturbance of atmospheric turbulence has the ability to fill the intensity hole with optical energy. As the turbulence strength continues to become strong, there exists a minimum value of R_5%, and then R_5% tends to rise because of the serious beam spreading due to strong atmospheric turbulent effects.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Plots of R5% versus turbulence strength for m = 1 and m = 2.

We use the effective beam radius to describe the beam spreading of a vortex beam propagating in spite of the existence of an energy hole. The effective radius can be expressed by

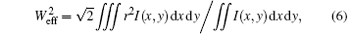
where I(x, y) is the intensity distribution. Figure 7 displays the short-term and long-term effective beam radii of vortex beams versus turbulence strength with different topological charges. We can see that the effective radius of a vortex beam with larger topological charge is greater than with a smaller topological charge. The beam spreading of the vortex beam may due to two reasons: the intensity-hole effect and the turbulent effect. Although a strong turbulent effect can fill the intensity hole with energy, the spreading of the vortex beam is also larger than that with no vortex phase. This can also be seen from Fig. 5.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Plots of short-term (a) and long-term (b) effective beam radii of vortex beams versus turbulence strength with different topological charges.

The wandering of the beam centroid is defined by the beam wander variation, which can be described by the following expression:

where I(ρ ) is the intensity distribution. The centroid (x_c, y_c) of the beam pattern can be expressed by

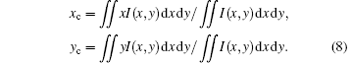
The beam wander variation can then be expressed as

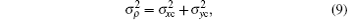
where and are the variations of x_c and y_c, respectively.

Figure 8 displays the RMSs of beam wander variation as a function of turbulence strength with different topological charges. It shows that topological charge has no evident influence on beam wandering and beam wander variations of vortex beams of different topological charges are almost equal to those of a Gaussian beam with no vortex phase.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Plots of beam wander variance versus turbulence strength with different topological charges.

The propagation properties of Gaussian vortex beam are quietly different from those of a Gaussian beam without a vortex phase. We use wave optics numerical simulation to study the intensity pattern, beam spreading, and wandering properties of a Gaussian vortex beam propagating in a turbulent atmosphere. The differences in propagation properties between a Gaussian vortex beam and a Gaussian beam are analyzed. The results show that in the center of beam pattern an intensity hole appears gradually as the Gaussian vortex beam propagates. The size of the intensity hole increases with the increase of topological charge but decreases with the growth of turbulence strength. This happens because the intensity hole could be filled with optical energy by the disturbance of atmospheric turbulence to some extent. The spreading of the Gaussian vortex beam is more serious than that of the Gaussian beam. However, the beam wander of Gaussian vortex beam is almost the same as that of the Gaussian beam. The vortex phase structure has no evident influence on beam wandering. All of these properties of the vortex beam can provide some theoretical base for the application of a vortex beam in free space communications, especially for intensity receival and detection.