Quantum computer and quantum information storage are built up from multiple microscopic physical systems. The most advanced experimental demonstrations at this time include trapped ions, ^[1] nuclear magnetic resonance, ^{[2, 3]} superconductors, ^{[4, 5]} and quantum dots in semiconductors.^{[6– 8]} With some of them, significant achievements in quantum computing have already been accomplished. Neutral atoms represent another promising approach, ^[9] which shares many features in common with trapped ion systems, including long-lived encoding of quantum information in atomic hyperfine states, week-decoupled with the environment. Using laser cooling techniques, countable numbers of neutral atoms can be trapped in an optical microscopic tweezer (far-off-resonance optical dipole trap), which can realize the full control of internal and external degrees of freedom.^{[10, 11]} A single atom trapped in microscopic tweezer can serve as a qubit.^{[12– 14]} Using two-dimensional arrays of refractive or diffractive micro-lenses, arrays of tweezers can be achieved, thus two-dimensional register of an atomic qubit can be obtained by loading a single neutral atom into these individually traps.^{[15– 17]} Moreover, the neutral atoms of two qubits are excited to highly excited Rydberg states that can be used to implement the quantum controlled-CNOT gate or create the entanglement.^{[18, 19]} Arrays of individual neutral atoms in traps with strong interaction are promising candidates for quantum computing experiments and quantum information processing.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. (a) Schematic diagram of the experimental setup. APD: avalanche photodiode working in the photon-counting mode; IF: 852-nm interference filter; PM fiber: polarization-maintaining fiber. (b) Transferring single atom between the MOT and the optical microscopic tweezer. Step fluorescence signals are obtained from the trapped atoms, the background light in tweezer (COT) and MOT (C0), single-atom events (C1) and two atoms (C2).

A set of criteria for implementing a quantum computing device require many qubits to be initialized at the same time, which depends on preparation of many microscopic tweezers for single atom occupancy. Several approaches have demonstrated the ability to load a single atom into a single tweezer. However, when many microscopic tweezers immerse in a large size magneto– optical trap (MOT), due to the extremely small trapping volume of tweezer compared with the MOT size, loading the preset number of atoms from the MOT into the multiple and individual site demanded is difficult. Although some experimental results have been demonstrated, the loading process has not been experimentally studied in detail. In this work we study the dynamics of loading a single atom trapped in a large size MOT into a microscopic tweezer. To study the loading process, we load only one atom trapped in the MOT into a microscopic tweezer and monitor the dynamics. Moreover, we report the direct observation of dependence of loading probability on the geometric overlap between the MOT and tweezer centers.

A schematic diagram of the experimental setup is shown in Fig.  1(a). We control the background cesium atom number in the working area by light-induced atom desorption. In our MOT system cooling/trapping laser beams and repumping laser beams are provided by two homemade 852-nm grating external-cavity diode lasers in the Littrow configuration. The two pairs of beams in horizontal plane intersect with the glass cell at an angle of 60° . The cooling laser of the (6S_1/2F_g= 4)– (6P_3/2F_e= 5) transition is stabilized using the modulation-free polarization spectroscopic locking scheme. The repumping laser is locked to the (6S_1/2F_g= 3)– (6P_3/2F_e= 4) hyperfine transition using the radio-frequency modulation spectroscopic locking scheme. The magnetic field of the MOT is produced by a pair of water-cooled anti-Helmholtz coils. The supplied current of 20  A yields a gradient magnetic field of ~ 300  Gs/cm (1  Gs = 10^{− 4}  T). The fluorescence photons of the cold atoms are collected by a lens assembly with a numerical aperture of 0.29, and are then coupled into a fiber-coupled avalanche photo-diode (APD) that works in the photon-counting mode. The tweezer beam is provided by a homemade laser-diode-pumped Nd:YVO₄ single-frequency 1064-nm laser. The laser beam is tightly focused into a vacuum cell with a waist radius of 2.3  μ m using a lens assembly. The trap depth is ~ 1.5  mK with a laser power of 47  mW.^[20]

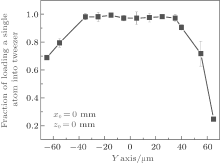
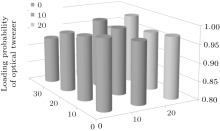
Due to the shallow trap depth of the tweezer, a standard method is to transfer the precooling atoms trapped in the MOT into the tweezer. The factor restricting the loading probability is the spatial arrangement of the two traps, which consists of the geometric overlap and the relative magnitude of the two traps. In our experiment, the trap size of the MOT is in a range of 60  µ m– 100  µ m depending on the magnetic field gradient, which is much larger than the size of the tweezer 2.3  µ m. The trap depth of the MOT as a function of magnetic field gradient, power, and detuning of cooling laser, is about hundreds of mK. The trap depth of the tweezer is on the order of mK, which scales with the intensity and wavelength squared. In general, efficient loading of a single atom trapped in MOT into a microtrap tweezer is hard for the extremely small volume and depth relative to the extent of MOT. As shown in Fig.  1(b), we show here that the trapped single atom in MOT can be transferred into the microscopic tweezer with almost unity probability. The tweezer is centered in the MOT region, overlapping about 0.2% of the MOT volume. The dependence of loading probability on the displacement between the tweezer and MOT center is shown in Fig.  2. It is evident that when the tweezer center is significantly displaced from the center of the MOT the loading probability still remains constant. This displacement is over ~ 10 times larger than the size of the tweezer. We also present the dependence of a typical one-dimensional and two-dimensional distribution of microscopic tweezers as shown in Fig.  3. The single atom loading, which is position-space-insensitive, means that one can prepare many singly occupied optical microscopic tweezers immersed in the MOT, which can be used to achieve the ensemble qubits in a straightforward manner.

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. Single atom loading probability versus displacement between the tweezer and MOT center. The 1/e trap size of the cold atoms is ~ 91  µ m with a magnetic field gradient ~ 175  Gs/cm. The tweezer focused spot overlaps about 0.2% of the MOT region. The error bars are caused partially by imperfect transferring technique and new loading events in the transferring process. The solid line is for guiding the eyes; X (Y, Z) is typical of three-dimensional space.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Experimental simulation of preparing single atom in a two-dimensional tweezer array. Individual traps in these patterns have a loading probability close to unity. The array of microscopic tweezers is simulated using a three-dimensional positioner with an adjusting accuracy of 0.5  µ m.

In the above section, we have experimentally demonstrated that the probability of loading a single atom into a tweezer is about ~ 100% , which is clearly insensitive to the relative size and the overlap of two traps. Here we give a qualitative analysis. Within Doppler cooling theory the light force acting on the cold atoms confined in the center of the MOT can be described by F= − α V − β x, which is a velocity-dependent cooling force and a position-dependent restoring force. Here α is the damping coefficient and β is the MOT spring constant proportional to magnetic field. Cold atoms in an MOT with a kinetic energy near ~ 100  µ K, decelerating force is smaller than restoring force which depends on the cooling laser detuning and position. The tweezer confines atoms by exerting a dipole force on the cold atoms, which increases with the trap depth. When a cold atom trapped in an MOT moves into the tweezer spot, the detuning to atom resonance is substantially larger than that only in an MOT due to the light shift of the tweezer, which means that trapping the atom in a tweezer is achieved by the larger dipole force rather than the restoring force.

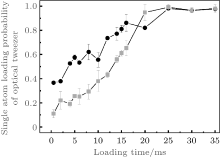
The loading probability is insensitive to center superposition of two traps but it depends on the loading time and magnetic field gradient, which allows us to control the restoring force of the MOT. The atomic cloud in the MOT is a nearly Gaussian density distribution, even for a few atoms or one atom in the MOT, thus when the centers of MOT and tweezer coincide, the loading efficiency is higher than in the case of displaced tweezer center with other parameters operating in the same conditions. This situation is also observed as shown in Fig.  4. At a relatively large displacement from the MOT trap center, a long loading time of the tweezer is needed to achieve a high loading probability.

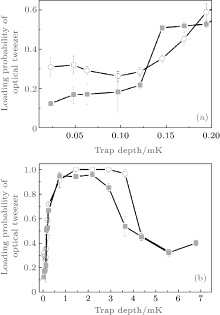
The above analysis shows that restoring force decreases with the detuning and increases with magnetic field gradient, whereas in the presence of the tweezer beam the dipole force may become dominant because of the light shift. An increase of the tweezer depth leads to a larger dipole force, which prevents atoms from being recaptured into MOT. We observe the same qualitative behavior but with different increase constants and offsets, which is shown in Fig.  5. A different offset value of loading probability arises from the magnetic field gradient. The loading probability first increases with the trap depth and then decreases in our experiment. The reason for the decrease behavior results from the noise heating of the tweezer beam.^[21]

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. Variations of loading probability of a single atom with loading time, for the cases of center superposition of two traps (black circles) and with 25-µ m displacements from the two traps centers (red squares). The error bar is for statistic error, which is caused partially by imperfect transferring technique and new loading events in the transferring process. Each experimental data point is from the accumulation of at least 100 sequences.

Fig.  5.

Figure Option ViewDownloadNew Window

Fig.  5. Plots of typical loading probability of tweezer versus the trap depth. (a) The red solid square denotes the ~ 300  Gs/cm magnetic field gradient for our MOT, and the blue empty circle represents the ~ 130  Gs/cm magnetic field gradient. At a low trap depth, the restoring force dominates the loading probability of trap. (b) With the increasing trap depth, the loading probability first increases and then decreases in our experiment. The decrease behavior is due to the noise heating of the tweezer beam. The error bar denotes the statistic error.

In this paper, we present a single cesium atom in a microscopic tweezer with a high loading probability. Our experimental results reveal the details of the trap loading processes that are usually masked when working with larger atomic ensembles. We identify the loading probability dependence. The single atom loading is insensitive to the size of the tweezer and center overlap of the two traps, which means that it is possible to extend this method for the preparation of many singly occupied microscopic tweezers immersed in an MOT.

The spatial insensitive loading implies that it is possible to simultaneously implement a large number of qubits in two- or three-dimensional arrays. The first problem is to suppress the stochastic loading and loss mechanisms in the MOT. The stochastic loading can be overcome by feedback-control of the loading and loss rates of MOT through external parameters. Employing controlled blue-detuned light assisted collisions can help realize only one of the collision partners being lost. More generally, a combination of a single-loss collisional redistribution process and feedback-control of the loading probability of MOT may substantially improve the loading probability. The deterministic preparation of a single atom into the tweezer is a necessary first step. A relevant issue in constructing a scalable quantum information processing device is the scalability of optical trapping to many qubits. The question of preparing single-atom occupancy in many tweezers is more challenging.