†Corresponding author. E-mail: shi_ying@jlu.edu.cn
*Project supported by the Science Fund from Jilin University, China (Grant No. 419080106440), the Chinese National Fusion Project for ITER (Grant No. 2010GB104003), and the National Natural Science Foundation of China (Grant No. 10974069).
Quasi-classical trajectory (QCT) studies on the stereodynamics of H + BrO → O + HBr reaction have been performed on the X1 A' state of ab initio potential energy surface by Peterson [Peterson K A 2000 J. Chem. Phys. 113 4598] in a collision energy range from 0 kcal/mol to 6 kcal/mol. Two of the polarization-dependent generalized differential cross sections (PDDCSs), (2 π/ σ)(d σ00/d ωt) (PDDCS00) and (2 π/ σ)(d σ20/d ωt) (PDDCS20) are considered. The rotational polarizations of these products show sensitive behaviors to the calculated collision energy range. Furthermore, in order to gain more knowledge about vector correlations, the product angular distribution, P( θr), and the dihedral angle, P( ϕr), are calculated, and the results indicate that both the rotational alignment and orientation of the product are enhanced as collision energy increases.
As catalytic cycle reaction of bromine-containing compounds plays a leading role in destructing the ozone, reactions of oxygen with bromides have been widely studied in recent decades.[1– 5] The O + HBr → OH + Br reaction which is considered to be a prototype of the reaction between oxygen and bromides has been investigated both experimentally and theoretically. For experimental aspects, employing the crossed molecular beams accompanied by mass spectrometric detection, Balucani et al.[6] have found that the yield of product BrO is about 0.14± 0.06. The rate constant and product yield of O + HBr → OH + Br reaction have been determined by Wine et al.[7] in a temperature range of 0 K– 297 K. In 1990, McRae and Cohen[8] performed a high-resolution investigation of v2 band of HOBr centered at 1162 cm− 1. Later in 2003, by using a high-resolution Fourier-transform absorption spectroscopy, Orphal et al.[9] reported the v3 bands of HOBr near 16 μ m with rotational assignments for more than 800 lines. Brouard and Valance[10] have reported the gas-phase UV/visible absorption spectrum which shows a slower photolysis rate of HOBr than previous results.
In the theoretical area, in 2000, a new accurate ground state ab initio potential energy surface was investigated by Peterson, [11] and the result is comparable to the previous experimental data. Using the quantum scattering method, Tang et al.[12] have studied the reaction probability, cross section, and the thermal rate constant of O + HBr → OH + Br reaction. Later, a three-dimensional (3D) time-dependent wave packet method[13] is used to study the ro-vibrational effect on the scalar properties of the reaction which has gained a sensitive result. Recently, we have reported a vibrational effect on the stereodynamics of the O + HBr → OH + Br reaction, which has indicated a vibrational dependency.[14] Moreover, reactions of hydrogen with halogen oxide, which are the reverse reactions of oxygen with halogen-containing species, have been investigated by using various theoretical methods in recent years.[15– 17] The collision energy effects have been studied by using the QCT method to calculate the reaction probability, integral cross section, and vector properties of H + OCl → OH + Cl reaction.[18] Influences of the collision energy and the isotope on reaction H + FO → O + HF have been examined by Han et al.[19]
As for the calculation methods, in recent years, the quasi-classical trajectory method has been widely used to investigate the stereodynamics of chemical reactions especially for those atom– diatomic reactions.[20– 26] Thus far, quite a lot of studies of the O + HBr → OH + Br reaction have been conducted. However, there has been reported neither experimental nor theoretical investigation of its reverse reaction H + BrO → O + HBr to date.
In this paper, the influence of the collision energy on the stereodynamics of H + BrO → O + HBr is presented by using the QCT method which has been further developed by Wang et al.[27] and Chen et al.[28] The angular distributions P(θ r) and P(ϕ r), the PDDCS00 and PDDCS20 are also calculated and discussed.
The centre-of-mass (CM) frame is adopted in our paper and depicted in Fig. 1.[29– 32] In the CM frame, the z axis is parallel to k which represents the reagent initial relative velocity vector. The y axis is perpendicular to the xz scattering plane which contains k and k′ (initial and final velocity vectors). The θ t is the angle between k and k′ , defined as cos θ t = (k· k′ )/(| k| · | k′ | ), which is the so-called scattering angle. The θ r is the polar angle which is also the angle between k and the rotational angular momentum vector j′ and ϕ r is the azimuth angle and the dihedral angle of the k– k′ – j′ correlation as well. The fully correlated CM angular distribution is written as the following equation:[33– 38]

Here, [k] = 2k + 1, the (1/σ )(dσ kq± /dω t) is the polarization-dependent generalized differential cross section (PDDCS) which is given by

where

The PDDCSs with q = 0 is given as

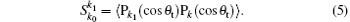
In our work, the two polarization-dependent generalized differential cross sections (PDDCSs), (2π /σ )(dσ 00/dω t) and (2π /σ )(dσ 20/dω t) are computed.
The angular distribution function P(θ r) can be expanded via the Legendre polynomials, the P(ϕ r) can be expanded in Fourier series, and the joint probability density function P(θ r, ϕ r) can be written as[35– 41]
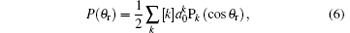
where
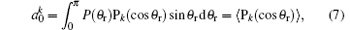
while k = 2 indicates the product rotational alignment, P2 is the second Legendre moment and the brackets represent an average over the distribution of j′ about k.
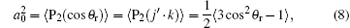

where
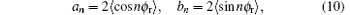
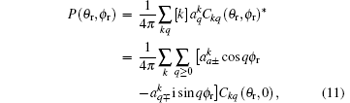
where
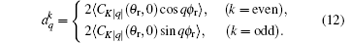
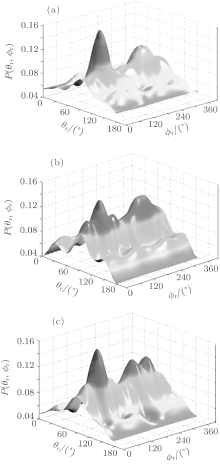
In our work, the P(θ r, ϕ r) is expanded to k = 7 to ensure the convergence of the results.
The potential energy surface (PES) in our present work is the ground state ab initio potential energy surface given by Peterson.[11] The multireference configuration interaction (MRCI) wave functions and basis sets of cc-pVDZ, cc-pVTZ, and cc-pVQZ are employed in the construction of the PES. It is worth emphasizing that there is deep potential well in the PES which may lead to a long-lifetime intermediate complex. A many-body expansion was employed in the analytical fitting written as:
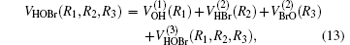
where R1, R2, R3 are the OH, HBr, and BrO separate distances, respectively. The 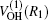
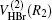
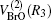
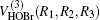
In this work, the QCT calculation details are described below. The collision energy is chosen to be in a range of 0 kcal/mol– 6 kcal/mol accompanied by running batches of 105 trajectories. The initial vibrational and rotational states are taken to be v = 0 and j = 0, respectively. An H– BrO internuclear separation is chosen to be 10 Å and an integration step size of 0.1 fs is used to assure the conservation of total angular momentum and total energy.
Due to the demand for a multiple perspectives observation, the stereodynamical results computed in our present work are all plotted in three dimensions. The polarization-dependent differential cross sections describe the k– k′ – j′ correlation and the scattering direction of the HBr product molecule. In this paper, the (2π /σ )(dσ 00/dω t) (PDDCS00) and (2π /σ )(dσ 20/dω t) (PDDCS20) are computed each as a function of scattering angle and collision energy for H + BrO → O + HBr reaction in a collision energy range of 0 kcal/mol– 6kcal/mol. The PDDCS00 is a simple DCS which describes only the k– k′ correlation or the scattering direction of the product and has no contact with j′ , which is depicted in Fig. 2(a). It is seen that with increasing the collision energy, it indicates a strongly forward and backward scattering though it is a weakly sideward scattering. Furthermore, the overall trend of the forward and backward scattering shows a rising behavior, which reveals the increase of the lifetime of the intermediate complex formed in the potential well. The PDDCS20 is associated with the expectation value of the second Legendre moment ⟨ P2 (j′ · k)⟩ . Obviously, the PDDCS20 demonstrates an opposite trend to the distribution of PDDCS00 which implies that j′ is aligned and perpendicular to k and the values of the distributions are almost negative. Meanwhile, the behaviors of the two PDDCSs also reflect the fact that the rotational alignment of the product becomes stronger as collision energy increases.
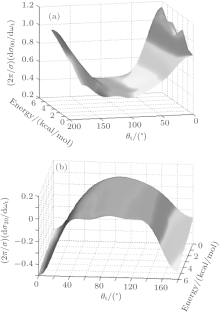 | Fig. 2. Two PDDCSs of collision energies at Ec = 0– 6 kcal/mol with (a) (k, q) = (0, 0); (b) (k, q) = (2, 0). |
Distributions of the product angular P(θ r) which represents the k– j′ correlation are displayed in Fig. 3. We can see that all peaks of P(θ r) are situated at θ r = 90° and shows a symmetrical distribution here which implies that the rotational angular momentum vector j′ is more favored to align strongly along the direction perpendicular to the direction of k. Meanwhile, with increasing the collision energy, the peaks become broader and values first increase and then show a series of small variations, indicating that the product alignment becomes weaker, which is consistent with the product alignment parameter ⟨ P2 (j′ · k)⟩ displayed in Fig. 4.
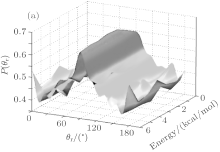 | Fig. 3. Distributions of P(θ r) reflecting k– j′ correlations at collision energies ranging from 0 kcal/mol to 6 kcal/mol. |
 | Fig. 4. Variation of rotational alignment parameter ⟨ P2 (j′ · k)⟩ with collision energy Ec in a range from 0 kcal/mol to 6 kcal/mol for the title reaction. |
Figure 5 illustrates the dihedral angle distribution P(ϕ r) which describes the k– k′ – j′ correlation. The computation values of collision energy Ec are in a range of 0 kcal/mol– 6 kcal/mol from the inside to the outside. As seen from Fig. 5, the distributions of P(ϕ r) are asymmetric with ϕ r = 180° at all calculated collision energies, which reveals a strong polarization of the angular momentum. We can also obtain that there is no clear peak, but the average values are located in the vicinity of ϕ r = 90° and ϕ r = 270° . Meanwhile, values at ϕ r = 90° are stronger than those at ϕ r = 270° which reflects the fact that the rotational angular momentum vector j′ is oriented along the positive direction of the y axis. This phenomenon may be attributed to its light– heavy– heavy (LHH) mass combination that is similar to the result given by Meng et al.[39] The reagent orbital angular momentum L transfers into the product orbital alignment, and j′ is independent of L, which can be explained by the impulsive model for A + BC → AB + C reaction suggested by Han et al.[40– 42] The angular momentum vector j′ of the project is given by
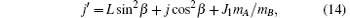
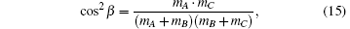
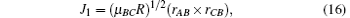
where L is the reagent orbital angular momentum, rAB and rCB are the unit vectors, R is the repulsive energy, and μ BC is the reduced mass of reagent molecule BC. The term Lsin2β + jcos2β is symmetric. The term J1 plays an important part in determining the rotational orientation. For the influence of the repulsive energy R, the term J1mA/mB indicates a prioritized direction which leads to the left-handed HBr product rotation in the plane parallel to the k– k′ scattering plane.
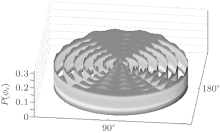 | Fig. 5. Dihedral angle distribution of P(ϕ r) with respect to the k– k′ plane, displayed in a reagent collision energy Ec (in a range of 0 kcal/mol– 6 kcal/mol) from inside to outside. |
In order to have an overall observation for the angular momentum polarization, the distributions of P(θ r, ϕ r) with the effect of the collision energy are shown in Figs. 6(a)– 6(c). For saving the space and without loss of generality, we only display the distributions with peaks and valleys at collision energy Ec = 0, 3, and 6 kcal/mol. As seen in Fig. 6, there are two main peaks at (90° , 90° ) and (90° , 270° ) which are consistent with the above-mentioned investigations. Meanwhile, it also implies that the HBr molecules are strongly polarized in the direction perpendicular to the scattering plane and generally rotate in the plane parallel to the scattering plane.
Collision energy effect on the stereodynamics of H + BrO → O + HBr reaction is investigated on the ground state ab initio potential energy surface at Ec = 0kcal/mol– 6 kcal/mol. In this paper, we calculate the polarization-dependent generalized differential cross section and the angular distributions of P(θ r) and P(ϕ r). Since there is a deep potential well on the PES, it leads to the formation of a long-lifetime intermediate complex which is indicated as the variation of the forward and backward scattering. As collision energy increases, the behavior of PDDCS00 shows a rising strong scattering forward and backward trend, which means that the lifetime of the intermediate complex in the deep well increases. The PDDCS20 demonstrates that j′ is strongly aligned in the direction perpendicular to k. Distribution of P(θ r) illustrates that the rotational angular momentum vector j′ prefers aligning strongly along the direction perpendicular to the direction of k. The P(ϕ r) distribution shows an asymmetric behavior to the scattering plane and two peaks at ϕ r = 90° and ϕ r = 270° which indicates that j′ is not only aligned but also oriented along the positive direction of the y axis, which can be explained by the impulsive model. The results of P(θ r) and P(ϕ r) are confirmed by the distributions of P(θ r, ϕ r). In summary, the collision energy has relatively obvious effects on product polarization and angular distributions of the title reaction and also affects the intermediate complex formed in the deep well.
Many thanks to Prof. Han Ke-Li for providing the stereodynamics program. This article supported by High Performance Computing Center of Jilin University, China.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|