Cite this Article
Wu Dong-Lan, Tan Bin, Xie An-Dong, Yan Bing, Ding Da-Jun. Accurate calculation of the potential energy curve and spectroscopic parameters of X2Σ+ state of 12Mg1H* . Chinese Physics B, 2015, 24(4): 043401  
Permissions
Accurate calculation of the potential energy curve and spectroscopic parameters of X2Σ+ state of 12Mg1H*
Wu Dong-Lana),c), Tan Binc), Xie An-Dongc), Yan Binga),b)†, Ding Da-Juna),b)‡
Institute of Atomic and Molecular Physics, Jilin University, Changchun 130012, China
Jilin Provincial Key Laboratory of Applied Atomic and Molecular Spectroscopy, Jilin University, Changchun 130012, China
College of Mathematics and Physics, Jinggangshan University, Ji’an 343009, China

†Corresponding author. E-mail: yanbing@jlu.edu.cn

‡Corresponding author. E-mail: djund@jlu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grand Nos. 11147158, 91221301, and 11264020)

Abstract

High level calculations on the ground state of12Mg1H molecule have been performed using multi-reference configuration interaction (MRCI) method with the Davidson modification. The core–valence correlation and scalar relativistic corrections are included into the present calculations at the same time. The potential energy curve (PEC) of the ground state, all of the vibrational levels and spectroscopic parameters are fitted. The results show that the levels and spectroscopic parameters are in good agreement with the available experimental data. The analytical potential energy function (APEF) is also deduced from the calculated PEC using the Murrell–Sorbie (M–S) potential function. The present results can provide a helpful reference for the future spectroscopic experiments or dynamical calculations of the molecule.

Keyword: 34.20.Cf; 31.15.aj; 31.50.Df; 33.20.–t; multi-reference configuration interaction; potential energy curve; analytical potential energy function; spectroscopic parameters
1. Introduction

The MgH molecule has gained great attention in the astrophysical community in the past quarter century.[1] The visible emission of MgH was first observed in the sun, and it was then observed in many stars. Its quantitative observation was of practical interest as a probe of the relative abundances of magnesium isotopes in stellar atmospheres.[2, 3]

In the past few years, there have been quite a lot of studies of MgH molecule. In experiment, the far infrared spectra of magnesium hydride were measured by Leopold et al.[4] in 1986, who observed that the transitions can be reproduced within 1  MHz. Lemoine et al.[5] investigated the infrared diode laser spectra of MgH in 1988 and obtained some spectral lines of the transition band. Shayesteh et al.[6] observed several vibration– rotation bands and obtained 0– 4 levels, equilibrium bond distances, vibrational and rotational constants of MgH in 2004. Later, they used a Fourier transform spectrometer to measure the visible emission spectra of the MgH molecule and gained 0– 10 levels and several spectroscopic parameters in 2007.[3] With respect to theoretical study, MgH is quite a simple molecule with three valence electrons, a ground state, and several excited states, and has been studied using ab initio all-electron calculations during the 1970s. The vertical excitation energies of MgH were calculated using the multi-reference single and double configuration interaction method (MRDCI) by Bruna and Grein.[7] Mestdagh et al.[8] in 2009 investigated the potential energy curves (PECs) and molecular constants for all MgH from ground states up to the excited atomic configurations Mg (3s3d1D) + H (1s2S), and these calculations help to clarify the very complicated spectrum of MgH in the 3.5 × 104  cm1− 4.6 × 104  cm1 excitation range. In 2012, Mostafanejad and Shayesteh[9] calculated the PECs and transition dipole moments of MgH using multi-reference configuration interaction method with large active space and basis sets. In 2013, using the direct-potential-fit method, Henderson et al.[10] obtained an accurate PEC for the ground state that reproduces all the observed rovibrational energy levels within their experimental uncertainties of 0.005  cm− 1. There are some differences of energy levels and spectroscopic parameters from their experiment data, which may be caused because they did not take into consideration the core– valence correlation and scalar relativistic influence. Therefore, to improve the quality of spectroscopic parameters of the MgH radical, more accurate calculations should be performed.

In the present work, the PEC of ground state is calculated by the high-level ab initio configuration interaction method, which is extrapolated to the complete basis set (CBS) limit. In order to obtain the accurate PEC, the core– valence correlation and scalar relativistic corrections are also taken into account in our calculations. The spectroscopic parameters are determined from the calculated PEC. Finally, we fit the PEC into the analytical potential energy function (APEF) by using the Murrell– Sorbie (M– S)[11– 15] potential function, and determine the spectroscopic parameters by using the obtained APEF. These provide a convenient expression to build an analytical potential energy surface of the polyatomic system or to study the dynamics of the photo dissociation and photo association of the molecule.

2. Computational method
2.1. Technical details for the calculations of PEC

In the present study, the electronic structure calculations are carried out with the Molpro2010.1 site of the quantum chemical package designed by Werner et al.[16] The symmetry point group of MgH is C∞ υ , owing to the limitation of the Molpro program, all of the calculations are performed in the C2υ subgroup of the C∞ υ point group. The corresponding relationships between the irreducible representations of the C2υ and C∞ υ point groups are Σ + = A1, Π = B1 + B2, Δ = A1 + A2, and Σ − = A2. The state-averaged complete active space self-consistent field (CASSCF)[17, 18] approach is used to calculate the energies of the ground state of MgH, where the active space includes 3s3p atomic orbitals (AO) on a Mg atom and 1s AO on a H atom. Further, by utilizing the CASSCF energies as reference values, the energies of the ground state are computed with the internally contracted multireference configuration interaction (MRCI)[19, 20] method, including Davison correction (MRCI + Q), [21] which has been used for many diatomic molecules.[22– 26] The inner-shell 1s2 electrons of Mg are kept frozen, while the 2s22p6 electrons of Mg are correlated to account for the core– valence correlation. That is to say, a total of 11 electrons in MgH (excluding 1s2 electrons of Mg) are correlated in the MRCI + Q calculations.

To improve the quality of the spectroscopic parameters, the core– valence correlation and scalar relativistic corrections are considered in the PEC calculations. In this work, core– valence correlation correction is included with a ccpCVTZ[27] basis set at the level of MRCI + Q theory, and its contribution is denoted as CV. Scalar relativistic correction is taken into account via the third-order Douglas– Kroll Hamiltonian (DKH3)[28, 29] approximation at the level of a cc-pVTZ basis set, and its contribution is denoted as DK. Here, the core– valence correlation and scalar relativistic corrections are applied across the entire PEC.

Three correlation-consistent basis sets: aug-cc-pVTZ (AVTZ) (AVQZ) and AV5Z, [30, 31] are used for the present extrapolation scheme (denoted as Q5). The extrapolation formula is written as[32]

Here, E(n) is the total energies obtained by the basis sets AVnZ (n = 3, 4, 5), ECBS is the total energy extrapolated to the CBS limit a, b, and c are the fitted parameters.

2.2. Vibrational levels

The rotational and vibrational energy levels are determined by solving the Schrö dinger equation of nuclear motion with the ab initio PEC, these calculations are carried out with the LEVEL 8.0 program package[33]

Here, v is the vibrational quantum number and J represents the rotational quantum number, G(v) is the vibrational level, Bv is the internal rotation constant, Dv and Hv are the first two centrifugal distortion constants.

2.3. Analytical potential energy function and spectroscopic parameters

The M-S function suggested by Murrell et al.[34] can be used to represent the two- and three-body terms of the potential energy surface.[35, 36] Here, we use the two-body term to express the interaction between Mg and H atoms. The expression is written as

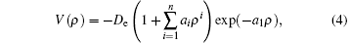
where ρ = R − Re, with R and Re being the internuclear distance and equilibrium bond length, respectively, De is the dissociation energy, ai and De are the parameters that can be determined by fitting. After trying a series of fittings, we find that the reasonable APEF of the ground state MgH molecule can be obtained when n equals 10. The root-mean-square (RMS) error can be used to assess quantitatively the quality of the fitting. The RMS can be calculated from

where VAPEF and Vab initio are the energies given by the fitting and the ab initio calculations, respectively, and N is the number of energy points to be used in the fitting.

Based on the relationship equations among spectroscopic parameters and APEF, the spectroscopic parameters can be calculated. Furthermore, the precision and credibility of the APEF can be testified by directly comparing the calculated spectroscopic parameters with experimental data. First of all, the force constants can be determined from the parameters of M-S potential energy function as[37]

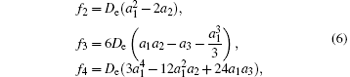
where f2, f3, and f4 are quadratic, cubic, and quartic force constants, respectively. Then the spectroscopic parameters are[37]

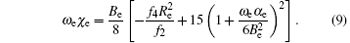
Here Be is the rigid-rotational factor, α e is the nonrigid-rotational factor, ω e is the harmonic vibrational frequency, and ω eχ e is the inharmonic vibrational factor.

3. Results and discussion
3.1. PEC of X2Σ + state

Using the MRCI+ Q method and different correlation-consistent basis sets, we calculate the PEC of the X2Σ + state for internuclear separations from about 1.2  Å to 6.05  Å in steps of 0.05  Å , except near the internuclear equilibrium position. A smaller step is adopted near the internuclear equilibrium position so that the properties of each PEC can be displayed more clearly. In the above calculation, the core– valence correlation and scalar relativistic corrections have been taken into account. The spectroscopic parameters (Re, De, and ω e) are listed in Table  1. As demonstrated in Table  1, we can see that the Re, De, and ω e values will change as the basis sets change. The differences in Re between the calculated results and experimental data are 0.0163, 0.0133, 0.0103, and 0.0088  Å . The values of De are 0.0181, 0.0407, 0.0499, and 0.0597  eV, and the values of ω e are 7.99, 5.79, 4.51, and 1.43  cm− 1 at the AVTZ, AVQZ, and AV5Z basis sets and the CBS limit, respectively. From the differences in Re, De, and ω e, we find that the errors become smaller as the basis set increases except De. In conclusion, we think that the present calculations at the CBS limit are close to the experimental results. Consequently, we use the PECs determined by the MRCI+ Q approach and extrapolation to the CBS limit for the present spectroscopic calculations.

Table 1. Equilibrium parameters of 12Mg1H with different basis sets.
3.2. Vibrational energy levels

Based on the obtained PEC, we solve the one-dimensional Schrö dinger equation of nuclear motion with the LEVEL 8.0 program package. For brevity, we collect and list the lower 11 bound vibrational levels of the X2Σ + ground state but omit the rotational levels in Table  2. It is found that the present computed vibrational levels and rotational constants are both in agreement with the available experimental data in the literature.[3] The least difference is 1.80  cm− 1 (v = 6), the largest deviation is 348.43  cm− 1 (v = 10). The reason for this is probably the anharmonic vibration. When v increases, the anharmonic vibration becomes more obvious. But the average percent error of vibrational levels is only 0.43%, which implies that the predicted levels are reliable. This is a helpful reference for future theoretical or experimental investigations.

Table 2. Vibrational levels and rotational constants for the X2Σ + state of 12Mg1H (in units of cm− 1).
3.3. Analytical potential energy function and spectroscopic parameters

To make the PEC more convenient for further applications, we construct APEF for the ground state of MgH with the M– S potential. The fitted parameters and RMS are presented in Table  3, and the fitted PEC are plotted in Fig.  1. As seen in Table  3, the RMS is only 0.004519  eV, which implies that the fitting process is of high quality and the present APEF can accurately reproduce the interaction energy between Mg and H atoms. From Fig.  1, the satisfactory fitting results also suggest that the M– S potential can effectively reproduce the short-range PEC. At the same time, we calculate the spectroscopic parameters with the APEF, and the results are listed in Table  4. From Table  4, it is found that some of spectroscopic parameters obtained by M– S potential are closer to experimental value than other theoretical data except De, which again shows the accuracy of the present calculations. The value of Re is 1.7293  Å , which is very close to the experimental value of 1.7297  Å , and the relative error is only 0.023%. The dissociation energy De differs from the experimental value by 0.0597  eV. The error is a little bigger than the other theoretical value, which may be the reason for the basis set extrapolation and no consideration of the spin orbit coupling. The fitted ω e is 1496.63  cm− 1, which is closer to the experimental value 1495.20  cm− 1 than the other results, the difference is only 1.43  cm− 1. Both ω eχ e and Be accord with the experimental value, with the relative errors being 0.539% and 0.046%, respectively. This implies that the theoretical level MRCI + Q/Q5 + CV + DK can give accurate results for both the spectroscopic and potential energy properties of the MgH molecule.

Fig.  1. Fitted and calculated potential energy functions for X2Σ + state of 12Mg1H.

Table 3. M-S APEF parameters for the X2Σ + state of 12Mg1H and RMS.
Table 4. Comparisons between spectroscopic parameters and available experiment and other theoretical results for the X2Σ + state of 12Mg1H.
4. Conclusion

In this work, the PEC of X2Σ + state of the 12Mg1H molecule are obtained at an MRCI + Q/Q5 + CV + DK theoretical level. The vibrational levels and the spectroscopic parameters are determined. It is found that the computational vibrational levels for the X2Σ + state of the 12Mg1H molecule are in good agreement with the theoretical ones. In addition, most of the fitted spectroscopic parameters are in accordance with the experimental data. The M– S potential can accurately reproduce the present short-range PEC, which is important for understanding not only the significant chemical processes in molecular clouds in astrophysics but also the relation to the composition of the molecular dissociation process. The accurate APEF can be conveniently used for investigating the photo association transition or the construction of APEF for a polyatomic system.

Reference
1 Fowler A 1907 Mon. Not. R. Astron. Soc. 67 530 DOI:10.1093/mnras/67.8.530 [Cited within:1] [JCR: 5.521]
2 Skory S, Weck P F, Stancil P C and Kirby K 2003 Astrophys. J. Suppl. Series 148 599 DOI:10.1086/apjs.2003.148.issue-2 [Cited within:1] [JCR: 16.238]
3 Shayesteh A, Henderson R D E, Le Roy R J and Bernath P F 2007 J. Phys. Chem. A 111 12495 DOI:10.1021/jp075704a [Cited within:3] [JCR: 2.771]
4 Leopold K R, Zink L R, Evenson K M, Jennings D A and Mizushima M 1986 J. Chem. Phys. 84 1935 DOI:10.1063/1.450445 [Cited within:1] [JCR: 1.578]
5 Lemoine B, Demuynck K, Destombes J L and Davies P B 1988 J. Chem. Phys. 89 673 DOI:10.1063/1.455188 [Cited within:1] [JCR: 1.578]
6 Shayesteh A, Appadoo D R T, Gordon I, Le Roy R J and Bernath P F 2004 J. Chem. Phys. 120 10002 DOI:10.1063/1.1724821 [Cited within:1] [JCR: 1.578]
7 Bruna P J and Grein F 2003 Phys. Chem. Chem. Phys. 5 3140 DOI:10.1039/b303698g [Cited within:1] [JCR: 3.829]
8 Mestdagh J M, Pujo P, Soep B and Spiegelman F 2009 Chem. Phys. Lett. 471 22 DOI:10.1016/j.cplett.2009.01.078 [Cited within:1] [JCR: 2.145]
9 Mostafanejad M and Shayesteh A 2012 Chem. Phys. Lett. 551 13 DOI:10.1016/j.cplett.2012.08.056 [Cited within:1] [JCR: 2.145]
10 Henderson R D E, Shayesteh A, Tao J, Haugen C C, Bernath P F and Le Roy R J 2013 J. Phys. Chem. A 117 13373 DOI:10.1021/jp406680r [Cited within:1] [JCR: 2.771]
11 Cao Y B, Yang C L, Wang M S and Ma X G 2013 Chin. Phys. B 22 123401 DOI:10.1088/1674-1056/22/12/123401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
12 Liu X Y, Yang C L, Wang M S, Ma X G and Liu W W 2012 Comput. Theor. Chem. 979 44 DOI:10.1016/j.comptc.2011.10.013 [Cited within:1] [JCR: 1.139]
13 Shi D H, Zhang J P, Sun J F, Liu Y F, Zhu Z L, Ma H and Yang X D 2008 Chin. Phys. B 17 3678 DOI:10.1088/1674-1056/17/10/025 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
14 Wu D L, Cheng X L, Yang X D, Xie A D, Ruan W, Yu X G and Wan H J 2007 Chin. Phys. 16 1290 DOI:10.1088/1009-1963/16/5/021 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
15 Wu D L, Xie A D, Yu X G and Wan H J 2012 Chin. Phys. B 21 043103 DOI:10.1088/1674-1056/21/4/043103 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
16 Werner H J, Knowles P J, Lindh R, Manby F R, Schütz M, Celani P, Korona T, Mitrushenkov A, Rauhut G, Adler T B, Amos R D, Bernhardsson A, Berning A, Cooper D L, Deegan M J O, Dobbyn A J, Eckert F, Goll E, Hampel C, Hetzer G, Hrenar T, Knizia G, Köppl C, Liu Y, Lloyd A W, Mata R A, May A J, McNicholas S J, Meyer W, Mura M E, Nicklass A, Palmieri P, Pflüger K, Pitzer R, Reiher M, Schumann U, Stoll H, Stone A J, Tarroni R, Thorsteinsson T, Wang M and Wolf A 2010MOLPRO, version 20101, a package of ab initio programs [Cited within:1]
17 Werner H J and Knowles P J 1985 J. Chem. Phys. 82 5053 DOI:10.1063/1.448627 [Cited within:1] [JCR: 1.578]
18 Knowles P J and Werner H J 1985 Chem. Phys. Lett. 115 259 DOI:10.1016/0009-2614(85)80025-7 [Cited within:1] [JCR: 2.145]
19 Werner H J and Knowles P J 1988 J. Chem. Phys. 89 5803 DOI:10.1063/1.455556 [Cited within:1] [JCR: 1.578]
20 Knowles P J and Werner H J 1988 Chem. Phys. Lett. 145 514 DOI:10.1016/0009-2614(88)87412-8 [Cited within:1] [JCR: 2.145]
21 Langhoff S R and Davidson E R 1974 Int. J. Quantum Chem. 8 61 DOI:10.1002/(ISSN)1097-461X [Cited within:1] [JCR: 1.306]
22 Li R, Zhang X M, Jin M X, Yan B and Xu H F 2014 Phys. Lett. 594 6 [Cited within:1] [JCR: 3.794]
23 Shi D H, Liu Q L, Sun J F and Zhu Z L 2014 Mol. Biomol. Spectros. 122 571 DOI:10.1016/j.saa.2013.11.098 [Cited within:1]
24 Li R, Zhai Z, Zhang X M, Jin M X, Xu H F and Yan B 2014 Chem. Phys. Lett. 599 51 DOI:10.1016/j.cplett.2014.03.017 [Cited within:1] [JCR: 2.145]
25 Liao J W and Yang C L 2014 Chin. Phys. B 23 073401 DOI:10.1088/1674-1056/23/7/073401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
26 Liu H, Feng H Q, Sun J F, Shi D H, Li W T and Zhu Z L 2013 Acta Phys. Sin. 62 013105 DOI:10.7498/aps.62.013105(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
27 Woon D E and Dunning T H 1995 J. Chem. Phys. 103 4572 DOI:10.1063/1.470645 [Cited within:1] [JCR: 1.578]
28 Douglas M and Kroll N M 1974 Ann. Phys. 82 89 DOI:10.1016/0003-4916(74)90333-9 [Cited within:1] [JCR: 0.25]
29 Hess B A 1986 Phys. Rev. A 33 3742 DOI:10.1103/PhysRevA.33.3742 [Cited within:1] [JCR: 3.042]
30 Woon D E and Dunning T H 1993 J. Chem. Phys. 98 1358 DOI:10.1063/1.464303 [Cited within:1] [JCR: 1.578]
31 Wilson A K, Woon D E, Peterson K A and Dunning T H 1999 J. Chem. Phys. 110 7667 DOI:10.1063/1.478678 [Cited within:1] [JCR: 1.578]
32 Müller T 2006 NIC Series 31 19 [Cited within:1]
33 Le Roy R J 2007LEVEL 8. 0 [Cited within:1]
34 Murrell J N, Carter S, Farantos S C, Huxley P and Varand as J C 1984 Molecular Potential Energy Functions Chichester John Wiley & Sons [Cited within:1]
35 Yang X, Yan B, Xu H F, Zhu R H, Zhang M X and Ding D J 2013 Chem. Phys. Lett. 577 22 DOI:10.1016/j.cplett.2013.05.035 [Cited within:1] [JCR: 2.145]
36 Wang S, Yu J K, Ding D J and Sun C C 2007 Theor. Chem. Accounts 118 337 DOI:10.1007/s00214-007-0262-1 [Cited within:1] [JCR: 2.233]
37 Zhu Z H and Yu H G 1997 Molecular Structure and Potential Energy Function Beijing Science Press [Cited within:2]
38 Shayesteh A and Bernath P F 2011 J. Chem. Phys. 135 094308 DOI:10.1063/1.3631341 [Cited within:1] [JCR: 1.578]
39 Huber K P and Herzberg G 1979 Molecular Spectra and Molecular Structure IV New York Van Nostrand Reinhold Company [Cited within:1]
40 Saxon R P, Kirby K and Liu B 1978 J. Chem. Phys. 69 5301 [Cited within:1] [JCR: 1.578]
41 Guitou M, Spielfiedel A and Feautrier N 2010 Chem. Phys. Lett. 488 145 DOI:10.1016/j.cplett.2010.02.031 [Cited within:1] [JCR: 2.145]