In recent years, the terahertz (THz) wave emission from atoms in intense laser fields has attracted lots of interest owing to its potential as a unique analytical and imaging tool for nonlinear and time-domain spectroscopy, security screening, biology and medicine, remote sensing and information, and communication technology.^[1]

It was found that the interaction of strong femtosecond tabletop laser field with the gas medium is responsible for the high-energy THz radiation.^{[1– 4]} There are a large number of theoretical approaches to account for the THz emission. The fundamental mechanism is described as the “ four-wave mixing” (FWM)^[5] and the transient plasma current^{[6– 9]} process. When a fundamental and a second harmonic laser field are mixed, the explanation is usually on the basis of the transient plasma current process in plasma^{[9– 17]} and semiconductor, ^{[18– 22]} where the THz emissions are due to the subsequent electron dynamics following ionization induced by the incident laser field in the matter. Nevertheless, the four-wave mixing process was less possible as a result of the nonlinear susceptibility of the third-order (χ ³), ^{[5, 23]} which is too small to play a crucial role in gases. Therefore, it is usually assumed that the plasma current is the main mechanism of the THz emission^[24] in gases.

The three-step model^{[25, 26]} which is used to explain high-order harmonic generation (HHG) of atom gases exposed to intense laser field has a close relation to the model of plasma current. The difference between the plasma current model and the three-step model is the following: the high-order harmonics generated from the atom are radiated in the process of an ionized electron recombining with the parent ion, while the THz wave is emitted by the transition between the electronic energy levels in the high-excited bound states and the braking radiation of the electron movement in the continuum states.^[5] When a multiphoton ionization process of an atom in strong laser fields is involved, ^{[1, 27, 28]} transitions among many intermediate states can occur. It is hard to describe this type of nonlinear process as a result of the distortion of the time-dependent wave function. However, we have found that the field-free wave function can perfectly describe the time-dependent wave function by choosing a set of basis functions which have ideal orthogonality and normalization.

Previous studies have shown that the efficient emission of the THz wave occurs when gas is driven by two-color laser pulses, ^[12] therefore, in the present paper, we will investigate THz wave emission from a quantum mechanical viewpoint by solving the 1D time-dependent Schrö dinger equation (TDSE) in a two-color laser pulse with different laser intensities and phase differences. We not only report the THz wave emissions computed from the time-dependent functions of the atom in a laser field but also identify the discontinuous part of THz originated from the transition of bound– bound states by using the projection method.

The theory is given as follows, based on solving the one-dimensional time-dependent Schrö dinger equation (TDSE) with a two-color laser pulse (in atomic units, unless otherwise stated):

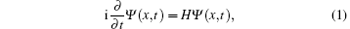
where H is the full Hamiltonian in dipole approximation,

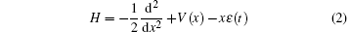
and V(x) is the model potential of the atom, a Guassian-enveloped laser pulse with 40-optical width, 106-fs full width at half maximum (FWHM) is used, and ε (t) is the laser fields composed of two colors:

where α is the ratio of the second harmonic laser amplitude to the fundamental one.

We used the split-operator method^{[5, 29, 30]} to compute the wave function from Eq.  (1). Once the wave function is obtained, the wave function in the velocity gauge can be easily determined by the mutual conversion of the wave function between coordinate and momentum space. The induced dipole moment in velocity form can be calculated as

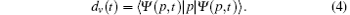
Numerical integrations are taken at time intervals of 0.1  a.u. and with a grid spacing of 0.1  a.u.

In order to analysis the emission of THz waves, the time-dependent solution Ψ (x, t) can be given in terms of expanding in a basis set

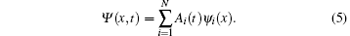
As suggested by Zhou et al., ^[31] the atomic eigenfunction in the field-free case, ψ _i can be expanded as follows:

where ϕ _n, constructed from the B-spline basis, is the bound state wave function of the field-free Hamiltonian, and the sine and cosine functions, and a truncated Fourier series that describes continuum states well is used in this basic set. The orthogonality and normalization of the basis functions ψ _i that are achieved by diagonalizing the field-free Hamiltonian are found to be satisfactory. Therefore, the probability amplitude of the i-th eigenstate, A_i(t), could be accurately obtained from the projection

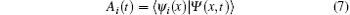
and the continuum functions, Ψ _c(x, t), are given as

The summation in Eq.  (8) is performed only for continuum eigenstates. Thus, the dipole moment including the continuum components can only be expressed as

where Ψ _c(p, t) is the continuum wave function in momentum space, obtained from Eq.  (8) by the Fourier transformation. The emission spectra of THz wave are computed by the fast-Fourier transformation of the time-dependent dipole moment:

Aiming to distinguish the relative contributions of the radiative transitions between the discontinuous and continuum parts in THz wave emissions, the time-dependent dipole moment is calculated by including only the continuum parts or discontinuous parts. For the continuum parts, the spectra are obtained

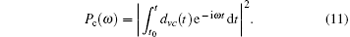
For the discontinuous parts, the spectra are obtained in a similar way, but the dipole moment only includes the bound– bound transitions.

In the simulation, we consider an argon atom exposed to the two-color laser field while the fundamental pulse has a central wavelength of 800  nm and the central wavelength of the second harmonic pulse is 400  nm. To illustrate the present numerical method we choose the soft Coulomb potential in Eq.  (2),

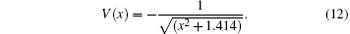
In our calculations, we typically take n₁ = 3, n₂ = 400 for x_max = 400 and an absorber of the form f_a(x) = cos[π (± x − 350)/2(x_max − 350)]^0.125 for the THz generation. To get an adequate frequency resolution in the THz range, we extended the propagation time to 4096 cycles.

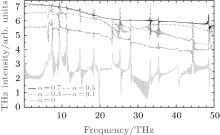
In Fig.  1 we show the THz spectra of an argon atom driven by a two-color laser pulse with an intensity of 1 × 10¹⁴  W/cm². It can be seen that the THz strength in a two-color field is enhanced by more than two orders compared to the single fundamental laser field. Our calculated results for different mixing of the fundamental laser field and the second harmonic field are also displayed in Fig.  1, in which the intensity of the second harmonic laser field is taken to be 0.1, 0.3, 0.5, and 0.7 times that of the fundamental one, while the intensity of the fundamental laser field is fixed. It is clear in Fig.  1 that the increase of the second harmonic field has a significant effect for the strength of THz emission. An important point in the figure is the appearance of a discontinuous THz wave besides the continuum background; however, all of the positions of those peaks with a different mixed laser field are at the same frequency. Thus the mixing laser fields have little effect on the position of these peaks for the same atomic system. In the following, we will separately study the characteristics of the continuum and the discontinuous parts of the THz emission.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. The THz emission spectra for the mixing laser fields with the fundamental intensity 1 × 1014 W/cm2 and α = 0, α = 0.1, α = 0.3, α = 0.5, α = 0.7, respectively and the phase difference φ = 0(all figures in this paper are log scale).

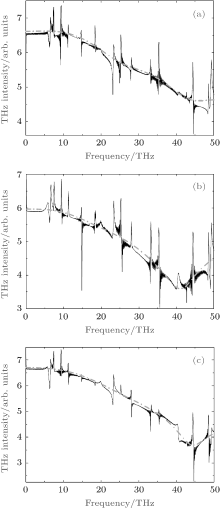
Firstly, we use Eq.  (9) to calculate the contribution to the THz emission for a continuum– continuum transition. The results that we have obtained are shown in Fig.  2. In order to understand the whole spectra, in the figure we also show some results with different intensities of the second harmonic field, as shown in Fig.  1. We can see from the figure that the transitions between the continuum– continuum parts play an important role in the THz emissions. The contour of the whole THz wave is determined by the continuum– continuum parts. In other words, the dominant contribution to the THz wave generation is given by the transitions among the continuum parts. This conclusion is the same as the transient current model.^[12] Because the THz wave emission in the current model comes from the transient current in air plasmas, while in our case the transition of the continuum– continuum states is the averaged moment of the photoelectron (see Eq.  (9)), which is proportional to the photoelectron current. Strictly speaking, both the bound states and the continuum states of an atom exposed to an intense laser field have no definition during the time propagation; however, because we expand the time-dependent wave function of an atom as a field-free basis function, the coefficients A_i(t) of the expansion functions in Eq.  (5) can still be understood as the amplitudes correspond to the continuum field-free states. Thus, we obtain consistent results for the continuum THz part with the whole time-dependent wavefunction (for instance, see Fig.  2). This suggests that we can use this method to analyze the sharp peaks of a THz wave, which are contributed by the transitions between the high excited bound states of an atom. More information about these will be presented later.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The THz emission spectra obtained from the whole wave function (solid line) and the continuum wave function only (dash– dotted line) for the fixing fundamental laser field with (a) α = 0, (b) α = 0.3, (c) α = 0.5, (d) α = 0.7, respectively, and phase difference φ = 0.

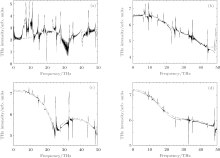
Next, we study the dependence of the THz emission on the phase difference between the fundamental and the second harmonic laser field. We calculate the THz emission which is based on the whole and continuum functions at different phase differences. The results are shown in Fig.  3. The results further confirm the concept that free– free transitions are the main process of THz emissions and the position of the maximum THz amplitude appeared at 0.8π , which is identical to the experimental results given by Lü et al.^[6] and Zhang et al.^[32] The reason for this can be explained by the symmetry breaking of the laser field.^{[12, 23]}

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The THz emission spectra obtained from the whole wave function (solid line) and the continuum wave function only (dash– dotted line) for the phase difference with (a) φ = 0, (b) φ = 0.5π , (c) φ = 0.8π , respectively and the ratio of the mixing laser amplitude α = 0.3.

The above results for the THz spectra shown in Figs.  1– 3 exhibit some sharp peaks besides continuum ones. It should be pointed out that the peaks originate from the highly excited bound– bound transition of an atom.^[5] We can analyze the origins of sharp peaks by using the same method applied to the continuum parts of a THz wave. Thus, the induced dipole for the bounds transition can be written as: d_e(t) = ⟨ Ψ _n(p, t)| p| Ψ _m(p, t)⟩ , where Ψ _n(p, t) and Ψ _m(p, t) represent the n-th and the m-th bound states, respectively. By using the same calculation method as the continuum part, we obtain the transition matrix elements between the different highly excited bound states. The matrix elements of the bound states are compared with the spectra from the whole wave functions. As shown in Fig.  4, the peaks position of the matrix elements can be matched with the peaks of the THz wave (the numerical results will be given in Table  1 below). Thus, each sharp line from 0  THz to 100  THz corresponding to the resonant transition between the specific high-lying Rydberg states can be identified accurately (note: n– m in Fig.  4 is the transition between the n-th and m-th states). Through our method, we can identify all of the sharp lines that are mainly produced from the transitions between the field-free bound states. From the figure, we can see that some peaks come from the transition between the adjacent Rydberg states and that some are from the separate Rydberg states with different parities. Our result for these sharp lines of THz wave have revealed that field-free wave functions can be used to accurately analyze the dynamic process of THz wave emission in a tunneling ionization regime, and even field-free states have no definition during the atom evolution in intense laser fields.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The emission spectra of the transition matrix element calculated from (a) the adjacent eigenstates and (b) the separate eigenstates for the laser field ε (t) = E0f(t)[cos(ω t) + 0.3cos(2ω t)].

In addition, in order to illustrate the accuracy of the transition matrix elements, the energy levels of the lowest 20 eigenstates given by diagonalizing the field-free Hamiltonian and the energy differences are shown in Table  1. The positions of these sharp peaks from the specific eigenstates transition are in good agreement with the corresponding energy differences that are highlighted by a bold slash in Table  1. It should be pointed out that a 1D model is often used to investigate the high-order harmonic generation of an atom in intense laser fields, and the 1D model results are in good agreement with those obtained from the three-dimensional model.^{[33, 34]} The process of THz emission is accompanied by the high harmonic generation [HHG], both THz and HHG are electromagnetic wave emissions. Thus, when studying the THz wave radiation we can employ the 1D model, which will greatly save on computing time.

Table 1.

Table 1.

Table 1. The energies (in unit a.u.) of the lowest 20 engenstates and the energy differences (in THz) between the different engenstates. En/a.u. (En– En− 1)/THz (En– En− 3)/THz (En– En− 5)/THz 0 – 0.57922462 1 – 0.2537544 2141.487 2 – 0.14264891 731.0374 3 – 0.08881415 354.2151 3226.739 4 – 0.0612313 181.4861 1266.738 5 – 0.04419508 112.0927 647.7938 3520.318 6 – 0.03369205 69.10647 362.6852 1447.938 7 – 0.02630525 48.60272 229.8019 765.5029 8 – 0.02125735 33.21352 150.9227 444.5014 9 – 0.01741749 25.26498 107.0812 288.2804 10 – 0.01461748 18.42317 76.90167 194.6108 11 – 0.01237358 14.76414 58.4523 140.2685 12 – 0.01066282 11.25624 44.44356 102.9221 13 – 0.00924005 9.361355 35.38174 79.06989 14 – 0.00811954 7.372531 27.99013 61.17744 15 – 0.00716069 6.308917 23.04282 49.06318 16 – 0.00637971 5.138616 18.82006 39.43766 17 – 0.00566237 4.719859 16.16739 32.90128 18 – 0.00498211 4.475893 14.33437 28.01582 19 – 0.00422076 5.009425 14.20518 25.65271

Table 1. The energies (in unit a.u.) of the lowest 20 engenstates and the energy differences (in THz) between the different engenstates.

The THz wave emission from a model argon atom has been investigated by solving the one-dimensional time-dependent Schrö dinger equation (TDSE). We calculated the spectra of THz wave emission of atom in intense laser field. Our results show that the THz spectra include both continuum and discontinuous parts. Based on the field-free basis functions that we have previously proposed, we studied the discontinuous part of the THz emission, as well as the continuum ones. Our results for continuum THz spectra are matched with those obtained from the total time-dependent wave function of the system. Furthermore, for the peaks of the discontinuous parts, we calculated the transition matrix elements between highly excited bound states in terms of our basis function. We found that the positions of all of the peaks obtained from the field-free states are in excellent agreement with those given by the total time-dependent wave function. Thus, our identification for the discontinuous part of the THz wave shows that field-free wave function can well describe the process of THz wave emission in a tunneling ionization regime.