†Corresponding author. E-mail: yangyj@jlu.edu.cn
*Project supported by the National Basic Research Program of China (Grant No. 2013CB922200), the National Natural Science Foundation of China (Grants Nos. 11274141, 11034003, 11304116, 11274001, and 11247024), and the Jilin Provincial Research Foundation for Basic Research, China (Grant No. 20140101168JC).
Using the time-dependent pseudo-spectral scheme, we solve the time-dependent Schrödinger equation of a hydrogen-like atom in a strong laser field in momentum space. The intensity-resolved photoelectron energy spectrum in above-threshold ionization is obtained and further analyzed. We find that with the increase of the laser intensity, the above-threshold ionization emission spectrum exhibits periodic resonance structure. By analyzing the population of atomic bound states, we find that it is the multi-photon excitation of bound state that leads to the occurrence of this phenomenon, which is in fairly good agreement with the experimental results.
With the rapid development of laser technology, the intensity of a laser field can be obtained to be close to or even larger than the intensity of the Coulomb field that the valence electrons in an atom can feel.[1] As the atoms and molecules interact with this intense laser pulse, the above-threshold ionization (ATI), high-order harmonic generation (HHG), non-sequential ionization, and other strong field phenomena can be observed.[2– 6] ATI is one of the typical unperturbed physical phenomena.
Recently, quite a few new phenomena have been found in research on ATI. With the development of the ultrashort laser technology, the carrier envelope phase (CEP) of the laser pulse plays a very important role in the process of ionization. In experiments, the ATI photoelectron spectrum can be used to measure the CEP of the laser pulse, [7, 8] and detect the internal structures of atoms and molecules.[9– 12] Utilizing the ultrashort intense infrared laser pulse[13, 14] to interact with atoms and molecules, new singular structures have been found in the low-energy part of ATI photoelectron spectrum, [15– 17] which is induced by the mid-infrared laser pulse and Coulomb long-range interaction.[18, 19] The development of the free electron laser and HHG technology provides a chance to study the interaction between high-frequency laser pulses. In the ATI photoelectron spectrum of the hydrogen atom under the action of high-frequency intense laser pulse it is found that with the increase of the intensity of the incident laser pulse, the peak shifts and a multi-peak structure occurs.[20, 21] This phenomenon can be attributed to the dynamic Stark effect and the interference between two electronic wave-packets.[22– 24] Li et al. discussed the resonance ionization via intensity-resolved ATI spectrum.[25] They used a quantum-trajectory Monte Carlo model to reproduce the measured photoelectron angular distribution of ATI.[26]
As the laser pulse interacts with the atom, the ground state electron may resonate with higher excited states, and a Freeman resonant peak can be observed in the low-energy region of photoelectron emission spectrum.[27, 28] Previous study has shown that this phenomenon is more sensitive to the CEP of the laser pulse, which can be used to detect the initial CEP of the laser pulse.[29, 30] This paper focuses on the study of the relationship between the resonance phenomenon, the structure of the ATI, and the population of the bound states of the system, which are observed within specific intensities.
To illuminate the above problems, according to the momentum space, we calculate the photoelectron spectra of hydrogen-like atom in different intensities by numerically solving the three-dimensional time-dependent Schrö dinger equation (TDSE), and find that with the increase of the intensity of incident laser pulse, the ATI peak structure changes from a single peak to a multi-peak and the resonant peak structure appears. However, if we further increase the intensity of the incident laser pulse, the ATI peak changes back to a single peak structure, and the resonant peak structure disappears, exhibiting a periodic resonance structure. By analyzing the population of the bound states, it is found that there exists a direct relation between the population of highly excited state and the resonance structure.
Atomic units are used throughout this paper unless otherwise indicated.
In order to investigate the photoelectron emission spectrum under the action of intense laser pulses through numerical simulation, we should first calculate the time-dependent wave-function of the electron in an intense laser field. In the coordinate space, the ionized electron will move to a zone which is far from the ions; therefore, in this case, larger computational space and more mesh grids are needed so as to make the results convergent. In this paper, based on the momentum space, the time-dependent pseudo-spectral scheme is used to solve the TDSE of the system, [31, 32] which can reduce the requirements for computational source on the promise of accurate calculation. In the velocity gauge, the coordinate space TDSE in the dipole approximation for an atom interacting with a laser field is given by
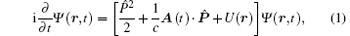
where c is the speed of light in vacuum, A(t) denotes the vector potential of the laser field, and U(r) represents the Coulomb potential of the atom. The momentum space wave function Φ (k, t) can be calculated from the Fourier transform of the coordinate space wave function Ψ (r, t) in the whole coordinate space as follows:
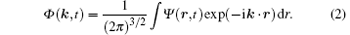
By applying Eq. (2) to Eq. (1), the TDSE in the momentum space can be obtained, which is an integro– differential equation given by
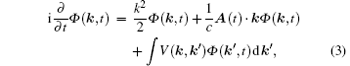
where V(k, k' ) is the momentum space Coulomb potential defined by
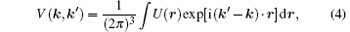
and for hydrogen-like system whose number of nuclear charge is Z, the above expression can be reduced to[33]

By utilizing the time-dependent pseudo-spectral scheme, we can solve Eq. (3) and obtain the time-dependent wave-function at any moment. Using the wave-function of the atom at the end of the laser pulse, and projecting it onto the eigen-state in the field-free case, we can calculate the excitation and ionization of the atom under the action of an intense laser pulse. After obtaining the final-state wave function of the system, we calculate the information about the ATI by utilizing the scheme proposed by Dionissopoulou et al.[34] At the end of the laser pulse, we can obtain the population of each state by projecting the eigen-state wave-function in the field-free case onto the final-state wave function. By projecting the scattered continuum state
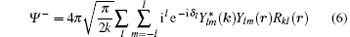
onto the wave function at the end of the laser pulse, if cl (ε , t) is the population amplitude of the normalized continuum state, the angular distribution of photoelectron can be obtained as
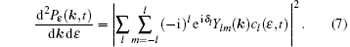
For the case of a linearly polarized laser pulse, it can be reduced to

and the corresponding single differential cross section is
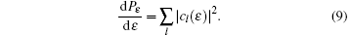
The laser pulse used in this paper is linearly polarized, whose incident direction is along the z axis, and whose electric field is

where A0 = E0/ω , E0 and ω are the peak amplitude and frequency of the laser electric field, respectively, and f(t) = sin2(ω t/2τ R) is the envelope of the laser’ s electric field, with τ R being the full width at half maximum (FWHM) of the laser pulse, which is selected as 10 optical cycles, and φ is the CEP, which is set to be 0. The wavelength of the incident laser pulse is 780 nm, and the ionization potential is 11.3 eV.
The intensity of the incident laser pulse changes from 2 TW/cm2 to 100 TW/cm2, and the variations of the total ionization and excitation with the intensity of the incident laser are investigated, and the results are shown in Fig. 1. It can be seen from the figure that with the increase of the incident intensity, the total ionization and excitation of atom increase on the whole; however, the peaked structures appear in some specific intensities. More importantly, for ionization and excitation, there exists a difference between their behaviors of peak structure: as for excitation, its peak structure is more obvious, and the intensities which the peak positions of the ionization and excitation correspond to are different, as shown by the arrow in the figure.
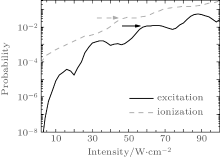 | Fig. 1. Variations of the total ionization and excitation probability with the intensity of the incident laser pulse. |
To further understand the change law of the ATI peak, we calculate the variation of the population of the bound state with the incident intensity, as shown in Fig. 2. In the figure, we present the variation of the probability of ionized electron with the incident intensity. It can be seen from the figure that the position where the peak of n photons disappears, calculated according to the formula, is in good agreement with that obtained from quantum calculation. More importantly, the disappearance of the ATI peaks continues the previous trend and extends to the negative energy area, and there is high population at the higher excited states as shown in the figure. We can also see from the figure that when population of the bound states is larger, the resonant multi-peak structure can be observed in the corresponding ATI peak, which is shown by the elliptic region in the figure. For the field strength at which the bound state of the atoms is resonance-enhanced, the population of the higher excited state is larger, and the corresponding total excitation of the atom is also enhanced, as shown in Fig. 1. For example, in Fig. 2, as the intensity changes between 60 TW/cm2 and 70 TW/cm2, the apparent multi-photon resonant excitation appears and the peak also appears in the corresponding product of total excitation, as shown by the solid black arrow in Fig. 1. It can be seen from Fig. 1 that the probability peak of the total excitation corresponds to the minimum of the total ionization. Therefore, we can deduce the cause which results in the difference between the intensities that the ionization and excitation peaks correspond to, i.e., as the higher excited states interact with the intense laser pulse, the energy level will move. Consequently, as the incident intensity meets the condition of multi-photon excitation, the excitation probability of an atom increases while the corresponding excitation probability is not that high. Therefore, as the incident intensity increases, it meets the condition of multi-photon ionization and the peaks will appear on the total ionization.
 | Fig. 2. Variations of population of continuous and bound states with the intensity of the incident laser. |
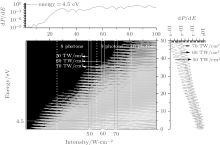
In order to make a comparison with the experimental results, the volume effect of laser pulse is taken into consideration in our calculation.[35] In Fig. 3(a), we present the ATI spectra as the intensities of the laser are 16 TW/cm2, 24 TW/cm2, and 40 TW/cm2, with the volume effect considered, which corresponds to the solid black curve, dash red curve, and dash– dot blue curve in Fig. 3(a), respectively. We can observe the change of ATI peak structure from the figure. When the intensity is 16 TW/cm2, the ATI peak structure has a single-peak. When the intensity is 24 TW/cm2, the ATI peak structure does not have a single-peak but changes into a multi-peak structure. If we further increase the incident intensity, the ATI peak structure changes back to a single-peak and the resonant structure disappears, indicating that this kind of resonant structure strongly depends on the intensity. In the experiments, we observe the ATI spectra of formic acid molecule whose ionization energy is 11.3 eV, [36] as shown in Fig. 3(b). The multi-peak structure is shown by the solid green arrow in Fig. 3(b). It can be seen from the figure that with the increase of the incident intensity, the ATI spectrum becomes identical to the theoretical result. By analyzing the population of the atomic bound state, we find that it is the multi-photon excitation of the bound state, leading to the occurrence of this multi-peak structure.
In order to understand the variations of the excitation and ionization probability with the intensity of the incident laser, we calculate the variation of the photoelectron spectrum with the intensity of the incident laser, as shown in Fig. 4. It can be seen from the figure that with the increase of the incident intensity, the cut-off position increases gradually. Since the influence of AC-STARK effect of laser field on the continuous state is large while that on the ground state is small, more energy is needed to make the atom ionized. The peak position of the ATI photoelectron emission spectrum is EATI = n × ω − Ip − Up, where Ip is the ionization potential of the atom, Up is the pondermotive energy, and n is the number of photons absorbed by the ground state electron. The Up increases linearly with the increase of the incident intensity. As a result, the ATI peak moves towards the low energy side. We present the position where the energy of the first ATI peak is zero as the number of photons absorbed by the ground state electron is n = 8– 10. With the increase of the intensity, the ATI peak exhibits the repetitive structures of single-peak and multi-peak, as shown in the panel on the right-hand side of Fig. 4.
 | Fig. 3. ATI spectra in different incident intensities, obtained from (a) the theoretical calculations and (b) the experimental measurements.[36] |
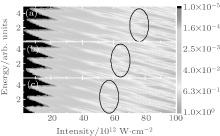
In addition, we investigate the photoelectron spectra of the atom for different wavelengths of the incident laser, as shown in Fig. 5. The wavelengths of the incident laser are selected to be 760 nm (Fig. 5(a)), 780 nm (Fig. 5(b)), and 800 nm (Fig. 5(c)), respectively. It can be seen from the figure that, within the same intensity and photoelectron energy range, different wavelengths show similar results: with the increase of the incident intensity, the ATI peaks move towards the low-energy side, the ATI peak that corresponds to intensity in which the first peak reaches zero energy starts to change from a single-peak structure to a multi-peak structure, as shown by the elliptic region in the figure, indicating that it gradually plays a dominant role in the process of multi-photon excitation of the high Rydberg state. The difference between the change laws of ATI peaks at different wavelengths lies in the fact that the slopes of the changes of ATI peaks with incident intensity are different, reflecting that, in the same intensity, different frequencies correspond to different values of Up.
In this study, based on the momentum space, we numerically solve the TDSE accurately, and systematically investigate the ATI emission spectra at different incident intensities. With the increase of the incident intensity, the ATI emission spectra exhibit periodic resonance structures of single-peak structure and multi-peak structure, respectively. By analyzing the change of the probability of the eigen-state at the end of the laser pulse with the incident intensity, the occurrence of the multi-peak structure can be attributed to the multi-photon excitation. With the volume effect considered: with the change of the incident intensity, the calculated ATI spectrum is identical to the experimental results.
We thank the High Performance Computing Center of Jilin University for supercomputer time.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|