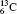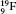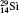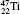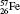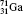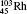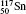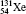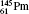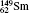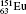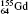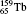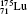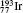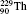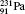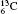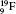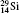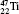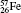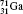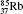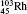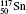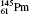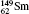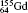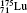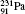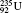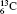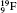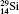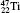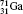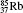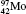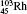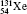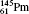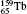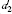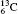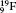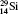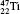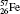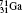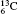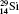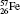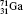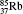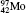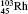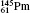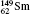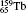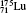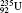†Corresponding author. E-mail: gediminas.gaigalas@tfai.vu.lt
‡Corresponding author. E-mail: Li_Jiguang@iapcm.ac.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11274254, 11147108, 10979007, U1331122, and U1332206) and in part by the National Basic Research Program of China (Grant No. 2013CB922200).
Weak- and hyperfine-interaction-induced 1s2s1S0 → 1s2 1S0 E1 transition rates for the isoelectronic sequence of He-like ions have been calculated using the multi-configuration Dirac–Hartree–Fock (MCDHF) and relativistic configuration interaction methods. The results should be helpful for the future experimental investigations of parity non-conservation effects.
Weak interaction effects in atomic physics play a very important role in searching for new physics beyond the standard model of elementary particles. There are a number of experimental and theoretical investigations of the parity-violation effects in heavy neutral atoms.[1, 2] However, correlation effects are the main source of uncertainty in theoretical results. Therefore, it looks promising to investigate relatively simple highly charged few-electrons ions in order to minimize the impact of correlation effects.
Gorshkov and Labzovskii̇ ̂ [3] and Labzowsky et al.[4] have proposed that the mixed hyperfine and weak-quenching can be used to test parity-violation effects. The one-photon transition 1s2s 1S0 → 1s2 1S0 of He-like ions is considered to be a good candidate for these tests and the relevant experiments will be carried out at GSI.[5] The transition is due to several competing processes (see Fig. 1). In the first process the 1s2s 1S0 state is mixed with 1s2p 3P0 due to the weak interaction between the electrons and the nucleus. The 1s2p 3P0 state, in turn, is mixed with 1s2p 3P1 and 1s2p 1P1 due to the off-diagonal hyperfine interaction opening the 1s2s 1S0 → 1s2 1S0 E1 transition. In the second process the 1s2s 1S0 and 1s2s 3S1 states are mixed due to the off-diagonal hyperfine interaction opening the 1s2s 1S0 → 1s2 1S0 M1 transition. The latter transition has recently been studied by Li et al.[6] The third and dominant 1s2s 1S0 → 1s2 1S0 decay channel is the two-photon 2E1 transition. Relevant data for the combined weak- and hyperfine interaction-induced 1s2s 1S0 → 1s2 1S0 E1 transition are however still insufficient and in response to this we have performed systematic calculations along the He-like iso-electronic sequence using the relativistic atomic structure package GRASP2K.
In the MCDHF method, the atomic state function (ASF) ψ (γ PJMJ) of a stationary state of an atom is expressed as a linear combination of symmetry-adapted configuration state functions (CSFs) Φ (γ pPJMJ), i.e.

where J is the total electronic angular momentum of the state, γ represents the electronic configuration and intermediate quantum numbers whereas P stands for the parity. The mixing coefficients cp and the one-electron radial wave functions, building the CSFs, are obtained in a self-consistent procedure by optimization of the energy functional based on the Dirac– Coulomb Hamiltonian (in atomic unit: a.u.)
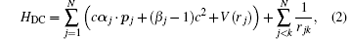
where V(rj) is the monopole part of the electron– nucleus interaction.[7, 8] The nuclear charge distribution is modeled by a two-component Fermi distribution. The MCDHF calculations were performed with the GRASP2K relativistic atomic structure package.[9, 10] In calculations of spin-angular parts of matrix elements the second quantization method in coupled tensorial form and the quasi-spin technique[11] were adopted.
In relativistic calculations the ASFs are given in j j-coupling. To adhere to the labeling conventions used by the experimentalists, the ASFs are transformed from j j-coupling to LS-coupling using the methods developed in Refs. [12] and [13]. The relativistic configuration interaction (RCI) method was also used to include the transverse Breit interaction and QED corrections: self-energy and vacuum polarization. The details of these corrections are discussed in Ref. [8]. In the presence of hyperfine interaction the coupled wave function of the total system of the electrons and the nucleus can be written as
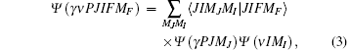
where the expansion coefficients are the Clebsch– Gordan coefficients, I is the nuclear spin, and F is the total angular momentum of the combined system. The wave function ψ (ν IMI) corresponds to the ground state of the nucleus. Taking the off-diagonal part of the hyperfine interaction into account, the total wave function of an atom can be expressed as
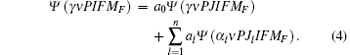
The off-diagonal hyperfine interaction is quite weak and the coefficient a0 of the dominant function can be set to 1 and expansion coefficients can be perturbatively approximated as
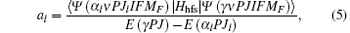
where Hhfs is the hyperfine interaction operator.[14] In this work we only include the nuclear magnetic dipole hyperfine interaction.
Due to the parity-violating exchange of neutral Z0 bosons between the electrons and nucleus, all atomic states are mixed with states of opposite parity. Spin-independent parity-nonconservating weak interaction between the electrons and nucleus is given by (in atomic unit: a.u.)[1, 2]
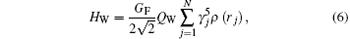
where GF is the Fermi constant, QW = Z(1 − 4sin2Θ W) − N the weak charge of the nucleus, γ 5 the Dirac matrix, and ρ (r) the normalized (to unity) Fermi nuclear density function. In our calculations we put sin2Θ W = 0.2312 for the Weinberg angle Θ W.[15] This interaction mixes parity of atomic states and also opens new decay channels. The total atomic wave function with mixed parity can be expressed as:
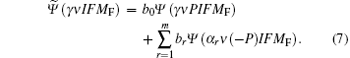
The parity non-conserving interaction, like the off-diagonal hyperfine interaction, is quite weak and the coefficient b0 of the dominant function can be set to 1 and expansion coefficients can also be perturbatively approximated as:
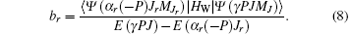
The rate of the spontaneous one-photon electric dipole (E1) transition between two atomic states with mixed parity is given by (in atomic unit a.u.):[16, 17]

where Q1 is the operator of the electric dipole transitions. Substituting Eqs. (4) and (7) into expression (9) and summing over the projections of the angular momenta gives
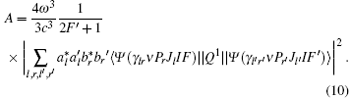
This expression can also be written (in unit s− 1) as:
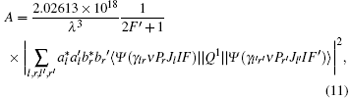
where λ is the wavelength in unit Ǻ for the transition. This perturbative formalism does not include the radiation-damping effects, which are important when the radiative line width is comparable to the separation between fine structure levels.[18]
The reduced matrix (submatrix) element of the electric dipole transition operator can be expressed as

The square of the absolute value of the last reduced matrix element is the line strength. Applying the Wigner– Eckart theorem, the matrix element of the weak interaction operator can be expressed as

where
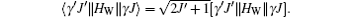
Using multi-configuration expansions, the reduced matrix elements of the general spherical tensor operator 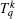

Reduced matrix elements of the one-electron operator between configuration state functions can be expressed as sums over elements involving single-particle orbitals
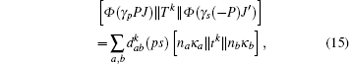
where 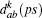

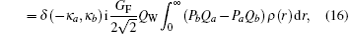
where 
For the generation of the MCDHF expansion (1) we used the active space approach. The energy functional on which the orbitals were optimized is defined according to an extended optimal level (EOL) scheme, where a linear combination of the seven lowest atomic states is used. The combination includes two even states with J = 0, one odd state with J = 0, two odd states with J = 1, one even state with J = 1 and one odd state with J = 2. CSFs are generated using active sets (AS) of orbitals. CSFs of the multi-configuration calculations include single and double substitutions from the 1s shell. The AS is labeled by an integer n and includes s, p, d, f, and g orbitals up to n. For example, the active set ASn = 4 contains s, p, d orbitals up to n = 4 and the 4f orbital. The active sets were extended to n = 6 for Z = 6− 61 and to n = 5 for Z = 62− 92 ions. At all steps, only new orbitals are optimized. For example, in the first calculation for the active set (AS2) all orbitals are optimized. In the next step the orbitals (1s 2s 2p) of AS2 are frozen and only the new orbitals (3s 3p 3d) from the active set AS3 are optimized.
Table 1 illustrates the convergence of the transition energies for the 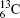
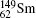
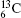
| Table 1. Transition energies in cm− 1 for 13C and 149Sm from calculations with increasing active sets including Breit interaction. Δ E1 = E (1s2 1S0) − E(1S2s 1S0), Δ E2 = E(1s2s 1S0) − E(1s2p 3P0), and Δ E3 = E(1s2p 3P1) − E(1s2p 3P0). QED corrections were calculated using active spaces of CSFs formed by the AS4. |
Also it should be mentioned that for ions with Z = 14, 26, 31, 37, 42, 45, 50, 54, 61– 63, 91, and 92, Coulomb and Breit interactions give incorrect positions of excited levels (comparing with data in Refs. [19] and [20]) and only when QED are introduced is the order correct. For ions Z = 6, 64, 65, 71, 77, and 90, the correct order of excited levels was obtained including the Breit interaction. Specific cases are ions with Z = 9 and 22. In the first case the energy levels are in the correct order when including the Coulomb interaction, but by adding the Breit interaction energies the order is incorrect. Including the QED effect we again get the correct energy spectrum. In the second case the correct order was obtained by including the Coloumb interaction and the Breit interaction; QED does not influence the order.
We also calculated the line strengths of the 1s2p 3P1 → 1s2 1S0 E1 transitions in the Coulomb gauge (Table 2):
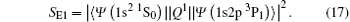
Line strengths are compared with data from Ref. [22] and the difference is at most 5.5%. This shows that wave functions are appropriate for weak and hyperfine interactions calculations.
| Table 2. The wavelengths λ in unit Å , for the 1s2s 1S0 → 1s2 1S0 E1 transition and line strengths SE1 Eq. (19) in atomic unit a.u. for the 1s2p 3P1 → 1s2 1S0 E1 transition of He-like ions. |
For the E1 transition 1s2s 1S0 → 1s2 1S0, as mentioned above, the important mixing of 1s2p 3P0 with 1s2p 3P1 is due to the off-diagonal hyperfine interaction and the mixing of 1s2s 1S0 with 1s2p 3P0 is due to the weak interaction. Mixing coefficients a1 and b of these interactions are given by
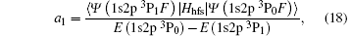
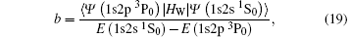
where F = I. The calculated off-diagonal hyperfine interaction matrix elements and corresponding mixing coefficients (a1), using obtained atomic wave functions, are presented in Table 3. Transition energies in the expressions above are calculated including the Breit interaction and QED effects. For elements 



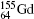
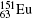
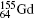
Table 3. Off-diagonal hyperfine interaction matrix elements 〈 | hhfs| 〉 1 (in atomic unit a.u.) and mixing coefficients (a1 and 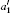 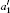 |
The calculated values of the weak interaction matrix element and corresponding mixing coefficients (b/i) are presented in Table 4. Due to the importance of the QED effects for the heavy ions, [23] transition energies are taken from accurate calculations by Plante et al.[19] and results of the Artemyev et al.[20] The first author included the QED effect of order (Zα )3 and some terms of (Zα )4, and the second author evaluated terms complete through order (Zα )4.
Table 4. The matrix element of the weak interaction operator (in 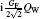 |
Compared with Plante et al.[19] and Artemyev et al.[20] our calculated QED contributions to the Δ E2 transition energies are too large. For example, the QED contribution for 
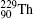

The values for the 

However, results with more accurate values of the energies[20] differ from the ones in Ref. [4]. In this table we also display the values of the weak- and hyperfine-interaction-induced 1s2s 1S0 → 1s2 1S0 E1 transitions rates

The agreement between our values (in the brackets) for the 
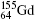
Due to the strong hyperfine-induced mixing between the 1s2p 3P0 and 1s2p 1P1 states for the low-Z ions[18] we also included the 1s2p 1P1 state in the calculations. Here is the given equation for mixing coefficients:
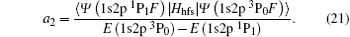
In Table 5 are given off-diagonal hyperfine interaction matrix elements 〈 | hhfs| 〉 2 (a.u.) and mixing coefficients (a2) between the 1s2p 3P0 and 1s2p 1P1 states. For the E (1s2p 3P0)– E (1s2p 1P1) transition energy QED effects are insignificant and the influence to the mixing coefficients a2 is less than 0.9%. Comparing transition rate (A1) (see Table 3) with A, it is clear that contributions of 1s2p 1P1 states are quite small (up to 3%).
Table 5. Off-diagonal hyperfine interaction matrix elements 〈 | hhfs| 〉 2 (in atomic unit a.u.) and mixing coefficients (a2 and 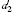  |
Table 6 given E1 1s2s 1S0 → 1s2 1S0 transition rates (A(WIT)) arising from weak and off-diagonal hyperfine interactions. A(WIT) are compared with transition rates of other 1s2s 1S0 → 1s2 1S0 decay channels: hyperfine-induced magnetic dipole transition rates M1 A(HIT) and rates of two-photon electric dipole decay 2E1 (A(HIT)). Figure 2 reflects the importance of the QED effect to the b/i mixing coefficients and transition rates A. Filled circles show results computed with QED and empty circles results without QED. Also there are results calculated using energies from Refs. [19] (square) and [20] (triangle). QED effects of order (Zα )4 for elements 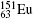

 | Fig. 2. Dependence of mixing coefficient b/i (absolute value) and transition rates A from number of neutrons (N). |
| Table 6. Comparison among hyperfine-induced M1 (A(HIT)), weak- and hyperfine-induced E1 (A(WIT)) and 2E1 (A(HIT)) 1s2s 1S0 → 1s2 1S0 transition rates (in unit s− 1). For the calculations of the transition rates of the weak and hyperfine-induced E1 transitions we used transition energies from Refs. [19] and [20]. |
To sum up, we have calculated weak- and hyperfine-interaction-induced 1s2s 1S0 → 1s2 1S0 E1 transition rates for the isoelectronic sequence of He-like ions using the multi-configuration Dirac– Hartree– Fock and relativistic configuration interaction methods. The comparison among our values and calculations of the transition rates of other 1s2s 1S0 → 1s2 1S0 decay channels are presented in Table 6. The calculated values differ from the previous calculations[4] for the 
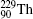
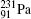
The authors are thankful for the high performance computing resources provided by the Information Technology Open Access Center of Vilnius University.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|