Cite this Article
Wei Zhao, Zhai Dong, Shao Xiao-Hong, Lu Yong, Zhang Ping. First-principles study of structural, elastic, and thermodynamic properties of ZrHf alloy* . Chinese Physics B, 2015, 24(4): 043102  
Permissions
First-principles study of structural, elastic, and thermodynamic properties of ZrHf alloy*
Wei Zhaoa), Zhai Donga), Shao Xiao-Honga)†, Lu Yongb), Zhang Pingb)‡
College of Science, Beijing University of Chemical Technology, Beijing 100029, China
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

†Corresponding author. E-mail: shaoxh@mail.buct.edu.cn

‡Corresponding author. E-mail: zhang_ping@iapcm.ac.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 51102009) and the Long-Term Subsidy Mechanism from the Ministry of Finance and the Ministry of Education of China.

Abstract

Structural parameters, elastic constants, and thermodynamic properties of ordered and disordered solid solutions of ZrHf alloys are investigated through first-principles calculations based on density-functional theory (DFT). The special quasi-random structure (SQS) method is used to model the disordered phase as a single unit cell, and two lamella structures are generated to model the ordered alloys. Small strains are applied to the unit cells to measure the elastic behavior and mechanical stability of ZrHf alloys and to obtain the independent elastic constants by the stress–strain relationship. Phonon dispersions and phonon density of states are presented to verify the thermodynamic stability of the considered phases. Our results show that both the ordered and disordered phases of ZrHf alloys are structurally stable. Based on the obtained phonon frequencies, thermodynamic properties, including Gibbs free energy, entropy, and heat capacity, are predicted within the quasi-harmonic approximation. It is verified that there are no obvious differences in energy between ordered and disordered phases over a wide temperature range.

Keyword: 31.15.A–; 62.20.–x; 63.20.–e; first-principles calculations; ZrHf alloys; disordered structure; special quasi-random structure; thermodynamic properties
1. Introduction

The group-IV transition metals, such as titanium (Ti), zirconium (Zr), hafnium (Hf), and alloys have attracted considerable interest for their extensive applications in many fields.[1] Zr, Hf, Zr-, and Hf-based alloys play a great role in the atomic energy industry and nuclear reactors due to their excellent hydrogen storage ability, their remarkable character of neutron control, and their strong resistance to corrosion.[2, 3] In previous work, phase diagrams and mechanical properties of Zr– H, Hf– H, and Zr– Hf– H systems have been thoroughly studied by experiments and theoretical calculations.[2, 4, 5] The Zr– C, Hf– C, and Zr– Hf– C hard refractory ceramic materials have also been investigated for their high melting points, decent refractory hardness and strong corrosion, and oxidation resistance.[6, 7] Within all this research, the Zr– Hf-based alloys are an interesting topic, where the Zr– Hf– X systems are mainly considered as ordered structures. Abriata et al.[8] discussed the phase diagram of Zr– Hf alloys at zero pressure and found two types of phases in the solid state, i.e., the hcp and bcc phases. A later calculation by Levy et al.[9] added a stable C32 structure of Zr2Hf when the Zr and Hf proportion is 2:1. However, there is no further information about this new phase, even about the lattice parameters. From another perspective, Bittermann et al.[6] investigated the crystallographic data of Zr and Hf metals and verified that Zr and Hf are completely soluble in one another, including the low-temperature hcp phase and high-temperature bcc phase. Therefore, a disordered phase should exist in Zr– Hf alloys.

In order to deal with the disordered phase, many approaches have been developed to model the solid solution alloys, such as the cluster expansion approach[10] and the special quasi-random structure (SQS) method.[11] Shin et al.[12] successfully calculated the enthalpy of mixed hcp-type Zr– Hf alloys using the SQS method, indicating that this method is suitable to deal with the disordered structure of Zr– Hf. Although the phase diagram and formation enthalpy of Zr– Hf alloys have been presented both by experimental and theoretical studies, the structure stability associated with elastic constants and phonon dispersion has seldom been addressed, which, as is fairly well known, is essential to the properties of these alloys. These conditions restrain science’ s understanding of Zr– Hf alloys deeply, and motivated us to investigate the SQS structure, elastic constants, phonon dispersion, and thermodynamic properties of Zr– Hf alloys in this paper, wherein we discuss the structural stability of the ordered and disordered phases thoroughly.

2. Theory and calculation methods

The first-principles calculations within density-functional theory (DFT) are carried out by the Vienna ab initio simulation package (VASP)[13] via the projector-augmented-wave (PAW) potential, and the generalized gradient approximation (GGA) in the Perdew– Burke– Erzerhof (PBE)[14] is used to describe the exchange and correlation effects. The cutoff energy is set to 500  eV to obtain the accurate total energy. The Brillouin zone (BZ) is sampled by 20 × 20 × 12 (2-atom cell), 10 × 20 × 12 (4-atom supercell), and 6 × 6 × 4 (16-atom cell) grids with Γ -centered k-point meshes, respectively. When the energy convergence becomes less than 1.0 × 10− 5  eV/atom, all the atoms are considered to be fully relaxed.

The elastic constants are calculated by means of a Taylor expansion of the total energy E(V, δ ), based on the following law:

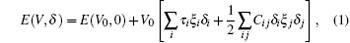
where E(V0, 0) and V0 are respectively the total energy and volume of the equilibrium cell with no strain, τ i is an element in the stress tensor, and ξ i is a Voigt factor.[15] The bulk modulus B of the alloys is obtained by the Voigt– Reuss– Hill (VRH) approximation[16]

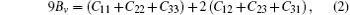
where Sij is an element of the inverse of the 6 × 6 matrix (Cij).

The Helmholtz free energy F(T, V) can be calculated by

where E(V) is the ground-state total energy at a given unit cell volume V, Fvib(T, V) is the vibrational energy of the lattice ions, and Fel(T, V) is the thermal electronic contribution to the free energy, which can be expressed by electronic entropy Sele(T, V) and energy due to the electron excitations Eele(T, V). Under quasi-harmonic approximation (QHA), [17– 21] the Fvib(T, V) can be calculated by

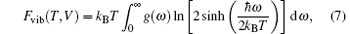
where ω is the phonon frequencies and g(ω ) is the phonon density of states (DOS). Finally, Sele(T, V) and Eele(T, V) can be measured by

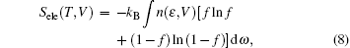
where n(ε , V) is the electronic DOS and f is the Fermi– Dirac distribution, and ε F in Eq.  (9) is the Fermi energy.

3. Results and discussion
3.1. Structure and elastic properties

Two lamella structures are employed to build the ordered structure of ZrHf alloys, as shown in Fig.  1. The visualizations of all the models are displayed by the VESTA code.[22] One of the two structures was frequently used in a previous study, [23, 24] and the other one is built in the same scheme. For Fig.  1(a), the Zr and Hf atoms are located at different positions in a “ standard hcp unit cell” , forming the layers along the C axis, and this structure can be called HCP-C. For Fig.  1(b), a 2 × 1 × 1 supercell of HCP-C is built and modified as the other unit cell of the ordered structure. These atoms can form a layer similar to HCP-C but along the A axis, and this structure is labeled HCP-A. To calculate the phonon dispersions of ZrHf alloys, we also prepared a 4 × 4 × 2 supercell for HCP-C and a 2 × 4 × 2 supercell for HCP-A. Each supercell of the two structures contains 64 atoms, as shown in Figs.  1(c) and 1(d), and the layers in the models can be clearly seen in these views.

Fig.  1. Schematics of ZrHf alloys for ordered structures in panels  (a) and (c) HCP-C structure and in panels  (b) and (d) HCP-A structure. The green balls are for Zr atoms and the brown are for Hf.

The special quasi-random structure (SQS) of ZrHf alloys is generated for the calculation of disordered structure. In general, eight-, sixteen- or thirty-two-atom models were used in the previous work of Zr-based alloys.[25] Using a Monte Carlo-based toolkit[26] provided by ATAT, the 8-atom, 16-atom, and 32-atom models are employed in our calculations. Since the core of the SQS model is the method of searching periodic cells based on clusters to replace the disordered structure through approaching the periodic cell correlation to the disordered structure correlation, all three structures are generated from the same clusters in this work, including all pairs shorter than 10  Å , triplets shorter than 6  Å , and quadruplets containing no pairs longer than 5.5  Å . Then, the energy minimizations of all the three structures are carried out. The minimized energy difference between the 16-atom and 32-atom models is about 1  meV per atom. Therefore, a 16-atom model is adopted in the following work, and its structure is shown in Fig.  2. To verify whether it satisfies the short-range statistics of an hcp random solution, the corresponding correlation function of the structure was also investigated, as listed in Table  1. As seen, the lattice vectors and correlation function of the structure are in agreement with the prior study.[12] The only difference between them is that some atoms of Zr and Hf exchange their positions. The energy calculated in this model differs only a little from the previously published one. After the investigation of the SQS model, a 2 × 2 × 1 supercell of this structure was prepared for the lattice vibration calculations, containing 64  atoms, like the lamella supercells.

Fig.  2. SQS of ZrHf alloys for the disordered structure with the green spheres for Zr atoms and the brown for Hf.

Table 1. Pair and multi-site correlation functions of the SQS. The degeneracy factor is listed in the square bracket next to Π k, m

The total energies of all the structures at different volumes are calculated and shown in Fig.  3. To avoid problems due to shear strain, all the models are relaxed according to a set of constant volumes before the calculations. All the curves almost overlap, so it is difficult to distinguish which structure is the most stable in terms of ground-state energy. Based on this, the calculated equilibrium structural parameters for all three models are listed in Table  2. For comparison, the calculated results of pure Zr and Hf are also listed in Table  2 along with the data reported in the literature. For the two pure elemental metals, the crystal constants and c/a ratios are all in agreement with the corresponding experimental results within a 1% error. Compared with the previous calculated results, the crystal constants of Zr in this work are much closer to the experimental data. Both the crystal constants of HCP-C and HCP-A are between the results of Zr and Hf, which obey “ Vegard’ s law.” [27] Considering that the SQS structure has a special unit cell, it is reasonable to compare the volumes rather than the lattice constants of these three structures. The calculated volume of SQS is 368.14  Å 3 in 16  atoms, and it equals 46.02  Å 3 in 2  atoms, which is in good agreement with the results of the two lamella structures of 46.00  Å 3, indicating that the ordered and disordered models are structurally similar.

Fig.  3. Calculated ground-state energy as a function of volume per formula unit cell.

The resistance and mechanical features of crystal under external stress or pressure can be measured through the elastic constants. In this work, we apply stress tensors with various small strains onto the optimized structures to calculate the elastic constants. The strain amplitude δ varies from − 0.03 to 0.03 with a step of 0.006. The results are presented in Table  2. As seen, all the elastic constants of the ordered and disordered models are between the values of pure Zr and Hf. The mechanical stability of all three structures can be obtained from restrictions based on the elastic constants data. Obviously, both the ordered HCP-C, HCP-A, and the disordered SQS are mechanically stable. In addition, the elastic constants and the bulk modulus B obtained from the VRH approximations[16] are shown in Table  2. Our calculated bulk modulus of pure Hf is in agreement with the previous theoretical study. Besides, the bulk modulus from VRH approximation of Zr is also very close to the experiment, indicating that our calculations of elastic constants and bulk modulus are reasonable. All the three bulk moduli B of ZrHf alloys are larger than the value of Zr and smaller than the result of Hf. This characteristic is like the elastic constants, and no significant difference is found among the three structures.

Table 2. Calculated lattice constants (a and c/a), elastic constants, and bulk modulus (B) of SQS, HCP-C, HCP-A, Zr, and Hf at no external pressure. For comparison, experimental results and other theoretical results are also listed.
3.2. Phonon dispersion and thermodynamic properties

The phonon curves and phonon DOS are measured by using density-functional perturbation theory (DFPT)[28] implemented in the PHONOPY code.[29] For the BZ integration, the 3 × 3 × 3 k-point meshes are used for the calculations of force constants. The pure metals use the same method as HCP-C to calculate the phonon curves and DOS for comparison and analysis. All the calculated results are shown in Fig.  4. Obviously, all three structures are stable at ground-state, and interaction between acoustic and optical branches exists among all the models, which is similar to TiZr alloys; [23] however, it differs in a way from the TiHf alloys, for which there is no interaction in alpha phase.[24] Compared with the phonon DOS of lamella structures and pure metals, the result of SQS is smoother, possibly resulting from the large cell (16 atoms in one cell) of the quasi-random model. Interestingly, the highest phonon frequency of Hf is about 4.7  THz, and the phonon dispersions of ZrHf alloys above this frequency are not empty. Consequently, it can be concluded that all the phonons at high frequency (> 4.7  THz) are provided by Zr, in accordance with the fact that ZrHf alloys can be regarded as an ideal solid solution.[6, 8, 30]

Fig.  4. Calculated phonon dispersions (left panel) and phonon DOS (right panel) of ZrHf alloys, Zr and Hf. Panels  (a)– (e) represent SQS, HCP-C, HCP-A, Zr, and Hf, respectively.

The thermodynamic properties, including the Gibbs free energy, the entropy, and the specific heat at constant volume (Cv) can be calculated by using QHA for all the structures, as shown in Fig.  5. Apparently, there is no crossing of Cv, entropy, and free energy of all the structures used in this work. Besides, the calculated Cv, entropy, and free energy of the three different alloys are almost identical. Compared with the properties of pure Zr and Hf, the thermodynamic properties of Zr– Hf alloys are between those of Zr and Hf, similar to the results of elastic properties, indicating that the ZrHf alloys are more like a mechanical mixture, regardless of whether the phase is ordered or disordered.

Fig.  5. Thermodynamic properties for HCP-C, HCP-A, SQS, Zr, and Hf as functions of temperature.

3.3. Stability analysis of ordered and disordered phases

Finally, we present in Fig.  6 the Gibbs free energy differences to analyze the stability of the three phases. The HCP-C is set to be zero for comparison. The difference values of free energy between all the phases are smaller than 0.5  meV/atom at the temperature of 0  K. With an increase of temperature, the curves of free energy difference become larger, with no indication that they will intersect at higher temperatures. Therefore, no spontaneous phase transition will occur among those three structures. When the temperature increases to 1000  K, the maximum difference of free energy reaches 5  meV. However, this energy is still so small that we propose that all of them can coexist in these alloys.

Fig.  6. Calculated Gibbs free energy differences of HCP-A and SQS with respect to HCP-C as a function of temperature by QHA at ambient pressure.

4. Conclusions

In summary, the structure, elasticity, phonon spectra, and thermodynamic properties of ZrHf alloys have been theoretically studied by the first-principles calculations. The volumes of SQS structure and ordered lamella structures are almost the same. The calculated elastic constants show that both ordered and disordered structures of the ZrHf alloys are mechanically stable. By comparing the elastic constants and bulk modulus, it is found that the compression resistances of these phases are nearly identical. The stable phonon dispersion curves indicate the thermodynamic stability of all the three structures of the ZrHf alloys. Based on the phonon frequencies, the thermodynamic properties, such as entropy, Gibbs free energy, and heat capacity of ordered and disordered phases have been theoretically calculated. Similar to the elastic behavior, the free energy, entropy, and heat capacity of the three different phases are almost identical, and the elastic and thermodynamic properties seem to be independent of atomic arrangements. No ordered– disordered phase transition can spontaneously occur within the temperature domain of phase stability, and the three phases can coexist in the alloys.

Reference
1 Spink D 1961 Ind. Eng. Chem. 53 97 DOI:10.1021/ie50614a019 [Cited within:1] [JCR: 2.206]
2 Dai Y, Yang L, Nie J, Fan K, Peng S, Long X, Zhou X, Bing W, Zu X and Gao F 2013 J. Alloys Compd. 581 404 DOI:10.1016/j.jallcom.2013.07.117 [Cited within:2] [JCR: 2.39]
3 Liu Y, Wang G, Wang J and Kang Z 2013 J. Alloys Compd. 555 381 DOI:10.1016/j.jallcom.2012.11.163 [Cited within:1] [JCR: 2.39]
4 Huang G, Long X, Peng S, Liang J and Yang B 2011 J. Fusion Energy 30 7 DOI:10.1007/s10894-010-9322-y [Cited within:1] [JCR: 1.0]
5 Zhou Y and Cheng Y S 2004 Health Phys. 86 155 DOI:10.1097/00004032-200402000-00006 [Cited within:1] [JCR: 1.017]
6 Bittermann H and Rogl P 2002 J. Phase Equilib. 23 218 DOI:10.1361/105497102770331703 [Cited within:3]
7 Lowther J E 2005 J. Phys. Chem. Solids 66 1064 DOI:10.1016/j.jpcs.2005.02.002 [Cited within:1] [JCR: 1.527]
8 Abriata J P, Bolcich J C and Peretti H A 1982 J. Phase Equilib. 3 29 DOI:10.1007/BF02873408 [Cited within:2]
9 Levy O, Hart G L and Curtarolo S 2010 Acta Mater. 58 2887 DOI:10.1016/j.actamat.2010.01.017 [Cited within:1] [JCR: 3.941]
10 Sanchez J M, Ducastelle F and Gratias D 1984 Physica A 128 334 DOI:10.1016/0378-4371(84)90096-7 [Cited within:1] [JCR: 1.676]
11 Zunger A, Wei S, Ferreira L G and Bernard J E 1990 Phys. Rev. Lett. 65 353 DOI:10.1103/PhysRevLett.65.353 [Cited within:1] [JCR: 7.943]
12 Shin D, Arr O Yave R, Liu Z and van de Walle A 2006 Phys. Rev. B 74 24204 DOI:10.1103/PhysRevB.74.024204 [Cited within:2]
13 Kresse G and Furthmüller J 1996 Phys. Rev. B 54 11169 DOI:10.1103/PhysRevB.54.11169 [Cited within:1]
14 Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 DOI:10.1103/PhysRevLett.77.3865 [Cited within:1] [JCR: 7.943]
15 Fast L, Wills J M, Johansson B and Eriksson O 1995 Phys. Rev. B 51 17431 DOI:10.1103/PhysRevB.51.17431 [Cited within:1]
16 Hill R 1952 Proc. Phys. Soc. Lond. Sect. A 65 349 DOI:10.1088/0370-1298/65/5/307 [Cited within:2]
17 Siegel A, Parlinski K and Wdowik U D 2006 Phys. Rev. B 74 104116 DOI:10.1103/PhysRevB.74.104116 [Cited within:1]
18 Sun X W, Zhang X Y, Zhang S H, Zhu Y, Wang L M, Zhang S L, Na M Z and Liu R P 2013 Chin. Phys. B 22 107105 DOI:10.1088/1674-1056/22/10/107105 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
19 Huang S, Zhang C H, Sun J and Shen J 2013 Chin. Phys. B 22 083401 DOI:10.1088/1674-1056/22/8/083401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
20 Wang J F, Chen W Z, Jiang Z Y, Zhang X D and Si L 2012 Chin. Phys. B 21 077102 DOI:10.1088/1674-1056/21/7/077102 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
21 Li Q, Huang D H, Cao Q L, Wang F H, Cai L C, Zhang X L and Jing F Q 2012 Chin. Phys. B 21 127102 DOI:10.1088/1674-1056/21/12/127102 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
22 Momma K and Izumi F 2011 J. Appl. Crystallogr. 44 1272 DOI:10.1107/S0021889811038970 [Cited within:1] [JCR: 3.343]
23 Wang B, Li W and Zhang P 2012 J. Nucl. Mater. 420 501 DOI:10.1016/j.jnucmat.2011.10.039 [Cited within:2] [JCR: 1.211]
24 Lu Y and Zhang P 2014 Comp. Mater. Sci. 82 5 DOI:10.1016/j.commatsci.2013.06.018 [Cited within:2] [JCR: 1.878]
25 Huang X, Zhang X, Zhang S, Zhu Y, Sa B, Ning J and Liu R 2014 Sci. Adv. Mater. 6 659 DOI:10.1166/sam.2014.1753 [Cited within:1] [JCR: 0.5]
26 van de Walle A, Tiwary P, de Jong M, Olmsted D L, Asta M, Dick A, Shin D, Wang Y, Chen L Q and Liu Z K 2013 Calphad 42 13 DOI:10.1016/j.calphad.2013.06.006 [Cited within:1] [JCR: 1.433]
27 Denton A R and Ashcroft N W 1991 Phys. Rev. A 43 3161 DOI:10.1103/PhysRevA.43.3161 [Cited within:1] [JCR: 3.042]
28 Gonze X and Lee C 1997 Phys. Rev. B 55 10355 DOI:10.1103/PhysRevB.55.10355 [Cited within:1]
29 Togo A, Oba F and Tanaka I 2008 Phys. Rev. B 78 134106 DOI:10.1103/PhysRevB.78.134106 [Cited within:1]
30 Thibon I, Ansel D and Gloriant T 2009 J. Alloys Compd. 470 127 DOI:10.1016/j.jallcom.2008.02.082 [Cited within:1] [JCR: 2.39]
31 Kittel C 1971 Introduction to Solid State Physics New York Wiley [Cited within:1]
32 Donohue J 1974 Structures of the Elements New York Wiley [Cited within:1]
33 Fisher E S and Renken C J 1964 Phys. Rev. 135 A482 DOI:10.1103/PhysRev.135.A482 [Cited within:1] [JCR: 6.583]
34 Zhang S, Zhu Y, Zhang X, Zhang S, Qi L and Liu R 2010 Comp. Mater. Sci. 50 179 DOI:10.1016/j.commatsci.2010.07.023 [Cited within:1] [JCR: 1.878]
35 Zhang S, Zhang X, Zhu Y, Zhang S, Qi L and Liu R 2012 Comp. Mater. Sci. 61 42 DOI:10.1016/j.commatsci.2012.03.057 [Cited within:1] [JCR: 1.878]
36 Brand es E A 1983 Smithells Metals Reference Book Stoneham Butterworth Publishers [Cited within:1]
37 Zhao Y, Zhang J, Pantea C, Qian J, Daemen L L, Rigg P A, Hixson R S, Gray G T, Yang Y, Wnag L, Wang Y and Uchida T 2005 Phys. Rev. B 71 184119 DOI:10.1103/PhysRevB.71.184119 [Cited within:1]