Cite this Article
Zhu Lin-Fan, Tian Hong-Chun, Liu Ya-Wei, Kang Xu, Liu Guo-Xing. Selection rules for electric multipole transition of diatomic molecule in scattering experiments* . Chinese Physics B, 2015, 24(4): 043101  
Permissions
Selection rules for electric multipole transition of diatomic molecule in scattering experiments*
Zhu Lin-Fana),b)†, Tian Hong-Chuna),b), Liu Ya-Weia),b), Kang Xua),b), Liu Guo-Xinga),b)
Hefei National Laboratory for Physical Sciences at Microscale and Department of Modern Physics, University of Science and Technology of China, Hefei 230026, China
Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei 230026, China

†Corresponding author. E-mail: lfzhu@ustc.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. U1332204, 11274291, and 11320101003).

Abstract

The knowledge of the energy level structures of atoms and molecules is mainly obtained by spectroscopic experiments. Both photoabsorption and photoemission spectra are subject to the electric dipole selection rules (also known as optical selection rules). However, the selection rules for atoms and molecules in the scattering experiments are not identical to those in the optical experiments. In this paper, based on the theory of the molecular point group, the selection rules are derived and summarized for the electric monopole, electric dipole, electric quadrupole, and electric octupole transitions of diatomic molecules under the first Born approximation in scattering experiments. Then based on the derived selection rules, the electron scattering spectra and x-ray scattering spectra of H2, N2, and CO at different momentum transfers are explained, and the discrepancies between the previous experimental results measured by different groups are elucidated.

Keyword: 31.10.+z; 34.50.–s; 31.15.xh; selection rule; molecular point group; electron scattering; x-ray scattering
1. Introduction

Energy level structures and dynamic parameters of atoms and molecules are the essential contents of the atomic and molecular physics. The energy level structures of atoms and molecules are almost entirely obtained by the spectroscopic experiments, either photoabsorption or photoemission spectroscopy. In spectroscopic experiments, the transition from the initial state to the final state in atom or molecule should obey the optical selection rules. For atoms and molecules the optical selection rules are described in detail in the corresponding textbook of the atomic and molecular physics.[1, 2] In fact, the selection rules in the spectroscopic experiments are the electric dipole selection rules, i.e., a transition can only occur between two states with a nonzero electric dipole moment:

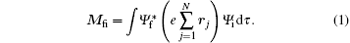
Shown in the spectroscopic experiments, the transitions have observerable strengths. In formula  (1), Ψ i and Ψ f are the wave functions of the initial and final states, respectively, rj is the position vector of the j-th electron in the atom or molecule, dτ represents the integration with respect to the position vectors and spins of all electrons, and 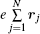is the operator of the electric dipole transition. In fact, in addition to the electric dipole transitions, there are magnetic dipole, electric quadrupole transitions, etc., but the probabilities of these transitions are very small in optical spectroscopy. So in the spectroscopic experiments about the neutral atom and molecule, they are difficult to observe.

Scattering experiment is another commonly used experimental method to study the energy level structures and dynamics of atoms and molecules. Compared with the spectroscopic method, the transition in scattering experiment does not need to follow the electric dipole selection rules. The reason is that in a scattering experiment the momentum and energy transferred from the incident particle to the atom or molecule are not one-to-one correspondence, i.e., for a definite energy state the energy transfer is fixed while the momentum transfer is determined by the scattering angle. Considering the fact that the photon momentum in the visible and VUV region is very small and can be regarded as zero, the exchanged momentum between photon and atom or molecule is near zero in the photoabsorption or photoemission process. Therefore, compared with the traditional optical experiment, the scattering experiment provides new information about the momentum transfer dependence behavior, i.e., the three-dimensional information about the excitation energy– momentum transfer– transition strength of atom and molecule. The scattering experiment has the unique advantages in detecting the optically forbidden transitions under the condition of the large momentum transfer, i.e., the electric monopole, electric quadrupole, and electric octupole transitions at the large scattering angles. Previous electron scattering[3– 6] and photon scattering[7– 10] experiments have confirmed this prediction. For the atom, its electric multipolarities can be elucidated easily.[1, 3– 5] However, for the diatomic molecule and linear triatomic molecules, we cannot find a comprehensive investigation about their selection rules for the electric multipolarities, and only fragmental discussions can be found in the literature.[11– 17] Because of the lack of the knowledge of the selection rules of electric multipole transitions of the diatomic molecule, some dipole-forbidden transitions were ignored inadvertently when analyzing the scattering spectra of diatomic molecules, which resulted in the inaccurate final results such as the discrepancies of the differential cross sections of C1 Π u of H2.[18] Actually, many previous experimental investigations[19, 20] ignored the contributions of the dipole-forbidden transitions of in H2.

From the above survey it can be learnt that the investigations about the selection rules for the electric multipole transitions, especially for the electric monopole, electric quadrupole, and electric octupole ones of diatomic molecules, are absent and unsystematic. Therefore, in this paper the selection rules for the electric multipole transitions of diatomic molecule are derived and summarized, and the valence-shell excitation spectra of H2, N2, and CO measured by the fast electron impact and inelastic x-ray scattering are explained.

2. Theoretical method

In this paper, we focus on the selection rules of electric multipole transitions in the fast electron scattering and inelastic x-ray scattering, in which the first-order Born approximation (FBA) is valid. Under the FBA, the corresponding transition probability between two states i and j is proportional to the square of the transition matrix element:[21]

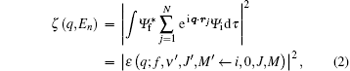
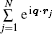
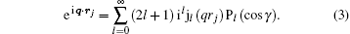
where ζ (q, En) is also called the inelastic squared form factor, En = Ei − Ef is the energy loss of the incident particle, which corresponds to the excitation energy of atom or molecule, q = ki − kf is the momentum transfer while ki and kf are the momenta of the incident and the scattering particles, respectively, and is the transition operator in the scattering process, which can be expanded as

Here, γ is the angle between q and rj, Pl (cos γ ) is the Legendre polynomial while jl (qrj) is the spherical Bessel function, and the terms of l = 0, 1, 2, and 3 correspond to the electric monopole, electric dipole, electric quadrupole, and electric octupole transitions, respectively. More higher-order electric multipole transitions can be determined easily with the recurrence relation. According to the Born– Oppenheimer approximation, the wave function of a molecule can be written as

Here, ψ e (r, R), ψ ν (R), and ψ JM (Θ , Φ ) are the electronic, vibrational and rotational wave functions, respectively, r is the electron’ s position vector whose coordinate system is fixed on the molecule, and the direction (Θ , Φ ) of the molecular axis refers to the laboratory coordinate system (X, Y, Z).

Herein we consider a molecular transition from the initial state (i, 0, J, M) to the final state (f, ν ′ , J′ , M′ ), where i and f represent the electronic states, while 0, J, and M are the vibrational and rotational quantum numbers of the initial state. For the neutral diatomic molecule at room temperature, generally the vibrational level of the initial state is ν = 0 and we write it directly as 0 here. ν ′ , J′ , and M′ are the vibrational and rotational quantum numbers of the final state. Substituting Eq.  (4) into Eq.  (2), the transition matrix element can be written as

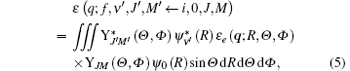
where ε e (q; R, Θ , Φ ) is the electronic transition matrix element and expressed as

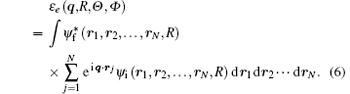
Since most scattering experiments cannot resolve the rotational states, averaging the population of rotational states and neglecting the weak dependence of ε e (q, R, Θ , Φ ) on different j, the transition matrix element can be written as

Here, ε e (q; R, Θ , Φ ) has the form of Eq.  (6). From Eq.  (3) we have

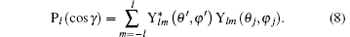
Here, (θ ′ , φ ′ ) and (θ j, φ j) are the directions of q and rj in the coordinate system fixed on the molecule. Since the spatial orientations of the molecules are random in most collision experiments, (θ ′ , φ ′ ) can take any values. It should be emphasized that (θ ′ , φ ′ ) can be converted into the laboratory coordinate system, and written as a function of (Θ , Φ ). Thus the squared form factor which represents the transition probability in a collision process can be written as

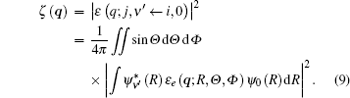
Here, the integration with respect to Θ and Φ means an average over the random orientation of the diatomic molecule. So the selection rules for a diatomic molecule in a collision process can be determined by the following transition matrix element:

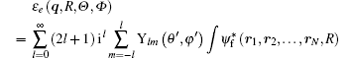
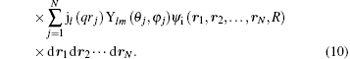
Herein Ylm(θ ′ , φ ′ ) comes from the random direction of q relative to the molecular axis as mentioned above. In Eq.  (10), the terms of l = 0, 1, 2, and 3 correspond to the electric monopole, electric dipole, electric quadrupole, and electric octupole transitions, respectively. For the higher order electric multipole transitions, it can be easily determined.

Although the integration in Eq.  (10) is very difficult to calculate, it is simple to judge whether the integral value is zero based on the knowledge of the group theory. Because the radial integration with respect to rj is not zero, we just need to judge the integration with respect to (θ j, φ j). For convenience, we rewrite the spherical harmonic functions Ylm(θ j, φ j) shown in Eq.  (10) as the real spherical harmonic functions which are commonly used in quantum chemistry[22] and shown in Table  1.

Table 1. Angular parts of the transition operators of the electric multipole transitions of the diatomic molecule as well as their irreducible representations.

The advantage in using the real spherical harmonic functions is that the transition operator belongs to the definite irreducible representation of the molecular point group. For example, Y00 or s is the totally symmetric irreducible representation for any point group, and Y10 or pz is Σ + irreducible representation in the C∞ v point group. Diatomic molecules belong to C∞ v or D∞ h point group. The corresponding irreducible representations of the transition operators are also listed in Table  1.[22] Considering that the initial and final electronic states of diatomic molecule correspond to definite irreducible representation, according to Eq.  (10), if the direct product of the irreducible representation that the initial and final electronic states and the transition operator belong to contain the totally symmetric irreducible representation, the electronic transition matrix element shown in Eq.  (10) is not zero. In mathematical formula, it is

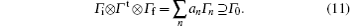
Here, Γ i and Γ f are the irreducible representations of the initial and final electronic wave functions respectively, Γ t is the irreducible representation of the transition operator, Γ n is an irreducible representation of the corresponding point group, the summation means the decomposition of the direct product with an being the expansion coefficients, and Γ 0 is the totally symmetric irreducible representation of the corresponding point group. Since the direct product of the molecular point group and decomposition of reducible representation can be found in the textbook of group theory or quantum chemistry, [23] herein we do not give the detailed description.

3. Results and discussion

The diatomic molecules with a center of symmetry, such as H2 and N2, belong to the point group D∞ h, while the diatomic molecules without a center of symmetry, such as CO and NO, belong to the point group C∞ v. According to Eqs.  (10), (11), and Table  1, we can determine the electric multipolarity of a transition between any two electronic states of diatomic molecules, and the corresponding selection rules for different electric multipolarities are listed in Table  2 and Table  3. It should be emphasized that the transitions should also obey the selection rule of the spin, i.e., the spin does not change in the scattering process.

Table 2. Transition selection rules of diatomic molecule belonging to point group C∞ v. The selection rules for the electric monopole, electric dipole, electric quadrupole, and electric octupole transitions are shown from left to right. X indicates the transition that is allowed while O represents the transition that is forbidden.
Table 3. The same as Table  2 but for the diatomic molecules belong to point group D∞ h.

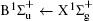
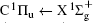
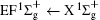
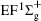
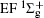
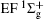
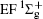
Figure  1 shows an inelastic x-ray scattering spectrum of H2 that is measured at SPring-8 by our group, and the experimental conditions are indicated in the figure’ s caption. The scattering angle of 18° corresponds to a squared momentum transfer of 0.35  a.u. (a.u. is the atomic unit), so the measured spectrum includes both the electric dipole-allowed transitions of and and the dipole-forbidden transition of . According to Table  3, besides the electric dipole component, and C 1Π u also contain the electric octupole components. From the spectrum unfolding it can be noticed that although is electric dipole-forbidden transition (i.e., electric monopole and quadrupole are allowed), its strength is not weak at q2 = 0.35  a.u. It can also be seen from Fig.  1 that the transitions in the energy loss spectrum overlap severely. Due to the complex energy level structures of a diatomic molecule, i.e., the electronic and vibrational states, it is very easy to ignore some transitions in the spectra analysis when lacking the systematic knowledge of selection rules, especially for the collision experiment where the energy resolution is not very good and the dipole-forbidden transitions are accessible. For example, in Fig.  1 the energy level interval between and C 1Π u is very small. So even if the is not taken into account in the spectrum unfolding process, the fitting results still reproduce the observed spectra very well. But ignoring the transition will result in the obtained strength of each vibronic level of C 1Π u being larger than its true value. Recently, Kato et al. measured the differential cross sections of the valence-shell excitations of H2, [18] and their experimental results of accord with the previous ones very well.[24, 25] But the differential cross sections of C 1Π u are significantly larger than the previous ones.[25] The reason for this discrepancy may be that in their data analysis they did not consider the contribution of the dipole-forbidden transition of , while in Ref.  [25] the contribution of was considered. Similarly, in some previous investigations[19, 20] the contributions of were also ignored.

Fig.  1. Inelastic x-ray scattering spectrum of H2 at an incident photon energy of about 9900  eV and a scattering angle of 18° . The unit 1  atm, = 1.01325× 105  Pa.

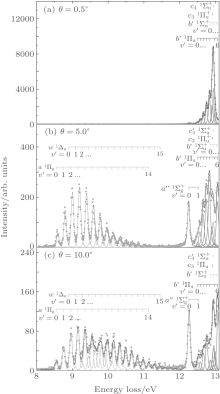
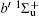
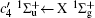
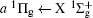
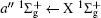
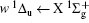
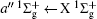
Figure  2 shows the electron energy loss spectra of N2 measured at an incident electron energy of 1500  eV and scattering angles of 0.5° , 5° , and 10° . Since the squared momentum transfer of 0.014  a.u. at 0.5° is very small, the optical approximation is approached. So the experimental spectrum at 0.5° only consists of the electric dipole-allowed transitions of b1Π u, , c31Π u, and in a range of 12.4  eV– 13.1  eV, while electric dipole-forbidden transitions of , , and are absent although they are observed clearly at larger momentum transfers as shown in Figs.  2(b) and 2(c). The relative intensities of , , and become larger and larger with increasing the scattering angle. It is clear in Fig.  2(c) that at a scattering angle of 10° , i.e., q2= 3.342  a.u., the strength of the electric dipole-forbidden transition is higher than those of most of the allowed ones, which is consistent with the tendency of dipole-allowed and dipole-forbidden transitions along the momentum transfer increasing.

Fig.  2. Electron energy loss spectra of N2, measured at an incident electron energy of 1500  eV and the scattering angles of 0.5° , 5° , and 10° , respectively. The corresponding squared momentum transfers at 0.5° , 5° , and 10° are 0.014  a.u., 0.841  a.u., and 3.342  a.u., respectively.

For heteronuclear diatomic molecule, the behaviors are similar. For example, 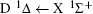of CO is an electric dipole-forbidden transition, but it is the electric quadrupole- and octupole-allowed ones. In the fast electron energy loss spectrum of CO at a large scattering angle of 7° is observed, [26] while it is absent at 0° .[27] This is in accordance with the theoretical predictions.

4. Conclusions

In the scattering experiment, the momentum transfer and energy transfer of the incident particle to the target are not one-to-one correspondence, so the electric dipole-forbidden transition can be observed at the large scattering angles. However, the selection rules about the dipole-forbidden transitions, i.e., the electric monopole, electric quadrupole, and electric octupole transitions, are fragmental and unsystematic. So in this paper, we deduce and summarize the selection rules for electric multipole transitions of diatomic molecules based on the knowledge of the molecular point group, and the results are summarized into Tables  2 and 3. On this basis, the inelastic x-ray scattering spectrum of H2 and the electron energy loss spectra of N2 are analyzed, and the electric multipolarities of the valence-shell excitations of H2 and N2 are elucidated. Furthermore, the discrepancies between the previous experimental results of H2 measured by different groups are elucidated.

Reference
1 Cowan R D The Theory of Atomic Structure and Spectra Berkeley University of California PressChaps.  4, 5, 6 [Cited within:2]
2 Herzberg G 1950 Molecular Spectra and Molecular Structure: Spectra of Diatomic Molecules New York Van Nostrand 138 [Cited within:1]
3 Cheng H D, Zhu L F, Liu X J, Yuan Z S, Li W B and Xu K Z 2005 Phys. Rev. A 71 032714 DOI:10.1103/PhysRevA.71.032714 [Cited within:2] [JCR: 3.042]
4 Zhu L F, Cheng H D, Yuan Z S, Liu X J, Sun J M and Xu K Z 2006 Phys. Rev. A 73 042703 DOI:10.1103/PhysRevA.73.042703 [Cited within:1] [JCR: 3.042]
5 Zhu L F, Yuan H, Jiang W C, Zhang F X, Yuan Z S, Cheng H D and Xu K Z 2007 Phys. Rev. A 75 032701 DOI:10.1103/PhysRevA.75.032701 [Cited within:1] [JCR: 3.042]
6 Suzuki T Y, Suzuki H, Ohtani S, Takayanagi T and Okada K 2007 Phys. Rev. A 75 032705 DOI:10.1103/PhysRevA.75.032705 [Cited within:1] [JCR: 3.042]
7 Xie B P, Zhu L F, Yang K, Zhou B, Hiraoka N, Cai Y Q, Yao Y, Wu C Q, Wang E L and Feng D L 2010 Phys. Rev. A 82 032501 DOI:10.1103/PhysRevA.82.032501 [Cited within:1] [JCR: 3.042]
8 Zhu L F, Xu W Q, Yang K, Jiang Z, Kang X, Xie B P, Feng D L, Hiraoka H and Tsuei K D 2012 Phys. Rev. A 85 030501 DOI:10.1103/PhysRevA.85.030501 [Cited within:1] [JCR: 3.042]
9 Kang X, Yang K, Liu Y W, Xu W Q, Hiraoka N, Tsuei K D, Zhang P F and Zhu L F 2012 Phys. Rev. A 86 022509 DOI:10.1103/PhysRevA.86.022509 [Cited within:1] [JCR: 3.042]
10 Peng Y G, Kang X, Yang K, Zhao X L, Liu Y W, Mei X X, Xu W Q, Hiraoka N, Tsuei K D and Zhu L F 2014 Phys. Rev. A 89 032512 DOI:10.1103/PhysRevA.89.032512 [Cited within:1] [JCR: 3.042]
11 Dunn G H 1962 Phys. Rev. Lett. 8 62 DOI:10.1103/PhysRevLett.8.62 [Cited within:1] [JCR: 7.943]
12 Goddard W AIII, Huestis D L, Cartwright D C and Trajmar S 1971 Chem. Phys. Lett. 11 329 DOI:10.1016/0009-2614(71)80499-2 [Cited within:1] [JCR: 2.145]
13 Wakiya K 1978 J. Phys. B: At. Mol. Opt. Phys. 11 3931 DOI:10.1088/0022-3700/11/22/020 [Cited within:1] [JCR: 2.031]
14 Cartwright D C, Trajmar S, Williams W and Huestis D L 1971 Phys. Rev. Lett. 27 704 DOI:10.1103/PhysRevLett.27.704 [Cited within:1] [JCR: 7.943]
15 Xu W Q, Sun J M, Wang Y Y and Zhu L F 2010 Phys. Rev. A 82 042716 DOI:10.1103/PhysRevA.82.042716 [Cited within:1] [JCR: 3.042]
16 Zhu L F, Xu W Q, Sun J M and Zhang W Y 2010 Chin. Phys. Lett. 27 113301 DOI:10.1088/0256-307X/27/11/113301 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
17 Wang Y Y, Sun J M and Zhu L F 2010 J. Chem. Phys. 132 124301 DOI:10.1063/1.3360311 [Cited within:1] [JCR: 1.578]
18 Kato H, Kawahara H, Hoshino M, Tanaka H, Campbell L and Brunger M J 2008 Phys. Rev. A 77 062708 DOI:10.1103/PhysRevA.77.062708 [Cited within:2]
19 Geiger J 1964 Z. Physik 181 413 DOI:10.1007/BF01380873 [Cited within:2] [JCR: 1.407]
20 Zhong Z P, Xu K Z, Feng R F, Zhang X J, Zhu L F and Liu X J 1998 J. Electron. Spectrosc. Relat. Phenom. 94 127 DOI:10.1016/S0368-2048(97)00106-0 [Cited within:2]
21 Inokuti M 1971 Rev. Mod. Phys. 43 297 DOI:10.1103/RevModPhys.43.297 [Cited within:1] [JCR: 44.982]
22 Achim Gelessus, Walter Thiel and Wolfgang Weber 1995 J. Chem. Educ. 72 505 DOI:10.1021/ed072p505 [Cited within:2] [JCR: 0.817]
23 Cotton F A 1990 Chemical Applications of Group Theory3rd edn. New York Wiley-Interscience PublicationChap.  4 [Cited within:1]
24 Srivastava S K and Jensen S 1977 J. Phys. B: At. Mol. Opt. Phys. 10 3341 DOI:10.1088/0022-3700/10/16/027 [Cited within:1] [JCR: 2.031]
25 Khakoo M A and Trajmar S 1986 Phys. Rev. A 34 146 DOI:10.1103/PhysRevA.34.146 [Cited within:3]
26 Zhu L F, Ren H F, Liu X J, Yuan Z S, Wu Y and Xu K Z 2005 J. Chem. Phys. 122 224303 DOI:10.1063/1.1927530 [Cited within:1] [JCR: 1.578]
27 Zhong Z P, Feng R F, Xu K Z, Wu S L, Zhu L F, Zhang X J, Ji Q and Shi Q C 1997 Phys. Rev. A 55 1799 DOI:10.1103/PhysRevA.55.1799 [Cited within:1] [JCR: 3.042]