The particle transport phenomenon induced by unbiased nonequilibrium fluctuations plays a crucial role in many physical and biological systems such as molecular motors, ^[1] nanoscale frictions, ^[1] surface smoothing, ^[2] optical ratchets, ^[3] particle separation, ^{[4, 5]} and artificial micro- and nanopores.^{[1, 6]} Most studies have been carried out with the consideration of the energetic barriers where the directed Brownian motion of particles is generated by unbiased nonequilibrium noise in the absence of any net macroscopic force and potential gradients, deterministic and random alike, together with spatial or temporal symmetry breaking. The energetic barrier depends on the variation of the thermodynamic potential, which plays an important role in the particle transport mechanism in solid-condensed systems. However, entropic barrier systems should be considered to explain the particle transport mechanism in some soft-condensed and biological systems since the presence of irregularities in the geometry of the boundaries may induce particle transport. Therefore, recently, there has been increasing interest in the transport properties of entropic barrier systems because of potential applications.

In order to reveal the physical mechanism of transportation in a barrier system, the energetics of this system have been investigated in a few seminal theoretical studies. Firstly, Magnasco^[7] showed that a Brownian particle, which is subjected to external fluctuations, can undergo a nonzero drift while moving under the influence of an asymmetric potential. The basic idea of Magnasco is that the efficiency can be optimized at a finite temperature. Based on an energetic analysis of Magnasco, energy conversion and particle current for energetic ratchet and entropic barrier systems have been investigated in detail.^{[8– 13]} Reguera et al.^{[14– 16]} used mesoscopic nonequilibrium thermodynamic theory to derive the general kinetic equation of a system. They also analyzed in detail the case of diffusion in a domain having an irregular geometry, in which the boundaries induce entropic barriers by coarsening the description of the dynamics. Ai and Liu^[17] showed that the convenient coupling of thermal noise and asymmetry in the boundaries of a tube can lead to a net current under asymmetric unbiased forces and in the presence of symmetric unbiased periodic force accompanied with a low external load such as friction.^[18]

The previous studies on efficiency and current are commonly based on the consideration of the energetic barriers under temporal forces. However, zero mean oscillating forces in entropic barrier systems may also induce the efficiency and current in which Brownian particles can be rectified by thermal noise and temporal forces. Oscillating forces have been used in the analyses of some entropic barrier systems. For example, it was shown that by exerting a sinusoidal force onto a carrier liquid, small particles can be separated from the large ones inside entropic barriers, which consist of asymmetric shaped pores.^{[4, 6]} Several groups^{[1, 19, 20]} prepared nanofluidic diodes by constructing conical nanopores and patterning them with asymmetric surface charges. They showed that these diodes can rectify diffusing ions having different polarities and their rectification powers are high. These are simple examples for the transports of Brownian particles in the entropic barrier profiles under unbiased oscillating forces. The transports in entropic barriers under oscillating forces may also appear in physical and biological systems as well as in the present examples.

Burada et al.^[21] showed that sinusoidal forces can lead to entropic stochastic resonance in barriers defined by quartic double well function, where the Brownian particles are driven by a sinusoidal force in the longitudinal direction and by a constant force in the transversal direction. In such entropic barriers in an optimized regime, cross-correlation between additive noise (i.e., intrinsic thermal fluctuation) and multiplicative noise (i.e., external environmental force) can lead to stochastic resonance.^{[22, 23]} Cross-correlation between two noises facilitates the particle transport and increases the efficiency in optimizing the amplitude and frequency of the driving force and temperature.^[23] A practical application of cross-correlated noises can be a Brownian motor constructed by two heat reservoirs and run under a sawtooth potential.^[24] It is shown that efficiency of this Brownian motor can be optimized by manipulating the amplitude of the driving force compatible with the temperature difference between hot and cold reservoirs.

In summary, understanding the particle transport under zero mean oscillating force in the entropic barriers may be important in order to reveal the transport properties of these systems. The present work is an extended study of efficiency and current in the case of entropic barriers under unbiased zero-mean oscillating forces. In this study we numerically show that an unbiased oscillating force in an entropic barrier can also lead to a net particle current and efficiency. Additionally, we find that the efficiency under an oscillating force is higher than that under a temporal force with the same amplitude in an optimized load, temperature and amplitude interval.

The rest of the present paper is organized as follows. Foremost, a theoretical background of stochastic dynamics accompanied with current and efficiency calculations under time varying forces are presented in Section 2. In Section 3, we present the change of current and efficiency with respect to load, temperature and amplitude of the force. We also discuss the optimized load, temperature and amplitude regions in this section. The conclusions and a summary of the results are given in Section 4.

The shape of the tube forming the entropic barriers can be defined as in Ref. [18]

where a is the amplitude of the barrier, b determines the half width at the bottleneck of the tube, L is the length of one period of the tube, and Δ is a parameter which defines the asymmetry of the tube. Here ω (x) defines the half width of the tube and it is a periodic function of x.

The equation of a Brownian particle moving along the axis of a three-dimensional tube is described by Reguera and Rubi^[14] and Reguera et al.^[15] as follows:

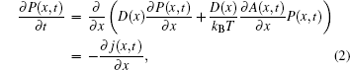
where A(x, t) is the free energy defined by A(x, t) = E – TS, here E = fx – F(t)x being the energy, S = k_B ln h(x) being the entropy, f being the constant load in the Brownian system, and F(t) being the external driving force, h(x) = π (ω (x)/L)² corresponding to the dimensionless width of the tube in three dimensions; P(x, t) is the probability density for the particle at position x, time t; j(x, t) is the probability current density; D(x) is the effective diffusion coefficient in three dimensions given as

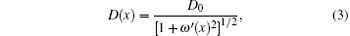
with D₀ = k_BT/γ , ω ′ (x) being the derivative of the shape of the entropic barrier that forms a tube structure defined by Eq. (1) and γ being the friction coefficient between particles and the carrier fluid.

It is assumed that in the stationary state the density P(x) = lim_{t→ ∞} P(x, t) and the probability current j = lim_{t → ∞} j(x, t) become constants of the transport. The explicit solution of Eq. (2) regarding the stationary state limit is presented in Refs. [16] and [18] by

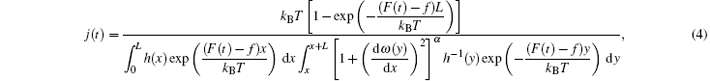
where α is equal to 1/2 in three dimensions. This solution is valid for an ensemble of Brownian particles at time t. At this point it is important to mention that here we have used the Fick– Jacobs approximation, which is invalid under strong forcing or wrinkled barriers. Moreover, the Fick– Jacobs approximation relies on the assumption of faster equilibration in the transverse direction than in the longitudinal transport direction.^[16] In our work we check the validity of the Fick– Jacobs description by comparing scaling parameter f = AL/k_BT, where A is the amplitude of the driving force, with the critical force value given by^[16]

Above this critical force, the Fick– Jacobs description will fail. Analytical expression of the f_c for the entropic barrier shape given by Eq. (1) is as follows:

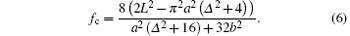
For the selected barrrier parameters given in Section 4, the critical force value is found to be f_c = 275.8, which is adequately higher than the scaling parameter f = 18.9 calculated by taking A = 1.5, L = 2π , k_B = 1, and T = 0.5.

The mean average current of all Brownian particles in the entropic barriers can be computed from

We note that P(x, t) and J(x, t) satisfy periodic boundary conditions as P(x, t + τ ) = P(x, t) and J(x + L, t) = J(x, t).

On the other hand, energy conversion efficiency η of Brownian particles is given in terms of the mean average work 〈 W〉 and the mean input energy 〈 E_in〉 by η = 〈 W〉 /〈 E_in〉 . According to the stochastic energetics, the heat δ Q = δ E_in − δ W is released to the heat bath during the period τ . For the transport process in the entropic barrier, the average input energy 〈 E_in〉 is given as^{[8, 9, 25]}

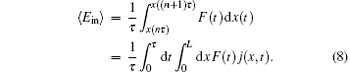
The entropic barrier under input energy rectifies the motion of Brownian particles in the time period τ . On the other hand, average work 〈 W〉 extracted from the input energy E_in during the period τ is given by^{[8, 25, 26]}

where V(x, t) is the periodic potential of the system defined by the shape of the entropic barrier. Except for the transient time, the potential satisfies the periodic boundary conditions as V(x, t + τ ) = V(x, t) and V(x + L, t) = V(x, t). In our study V only depends on the x axis. Finally, the efficiency can be given as^[8]

The average current in Eq. (7) and the efficiency in Eq. (10) can be simplified for a temporal force. However, in the case of an oscillating force, the solutions of these equations can be obtained numerically by using suitable integration methods.

In this study, we consider an entropic barrier, which has a shape given by Eq. (1). We compute the average currents and efficiencies of the Brownian particles in an entropic barrier for the temporarily symmetric unbiased force, sinusoidal force, amplitude modulated sinusoidal and cosinusoidal forces. These forces are given below respectively

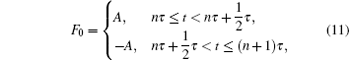
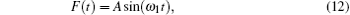
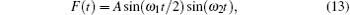
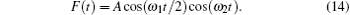
where A is an arbitrary constant, which defines the amplitude of the applied external force in the time interval [0, τ ] onto Brownian particles in the barrier. These forces are unbiased forces and they are symmetric under improper rotation. In other words, they preserve their forms after a mirror reflection along the vertical axis at t = τ /2 and a mirror reflection along the horizontal axis satisfying y = 0. The fundamental property of unbiased forces is that they have zero mean over one period as 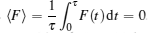. 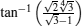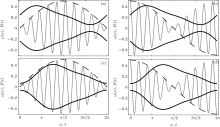From an experimental point of view, unbiased sinusoidal and modulated external forces can be obtained by ultrasonic perturbations or oscillating electric field in fluid system. Modulated oscillating function can be selected in order to mimic spatially varying isotropic frictional forces along the x axis inside the tube. However, when equation (1) is used for defining the entropic barrier, a phase difference appears between the applied force and the barrier periodicity as seen in Figs. 1(a) and 1(b). This causes an initial biased force in the barrier when an external force is applied, although the forces given in Eqs. (11)– (14) are unbiased. Therefore, we need to match the spatial periodicity of the barrier shape with the temporal periodicity of the applied force. In order to match the force and the barrier periodicity, the x value of at the extremum point of the barrier shape ω (x) given in Eq. (1) is subtracted from the argument x of the ω (x). This spatial translation in the barrier shape removes the phase difference between the force and the barrier periodicity. Hence spatial and temporal variables are matched on the same scale for L = 2π and τ = 2π as seen in Figs. 1(c) and 1(d), which guarantees that the force is initially unbiased throughout the spatial period of the entropic barriers. On the other hand, the angular frequency is ω ₁ = 1 when the period of the force is selected to be τ = 2π .

In order to show the relation between modulated forces and the shape of the barrier, the modulated one-period sine and cosine functions are plotted with the entropic tube in Figs. 1(c) and 1(d), respectively. In Fig. 1 the envelopes of the oscillating forces, which are depicted by dashed lines, are given in order to clarify the amplitude variations. When the shape of the tube described by Eq. (1) and amplitude modulation of the sinusoidal force are considered together, this system resembles a tube where the friction is high at the bottlenecks but low in the middle region. Consequently, the amplitude of the fluctuating force decreases at the bottleneck but increases in the middle region of the tube. Similarly in Fig. 1(d) one period of a modulated cosine function is plotted. On the other hand, the amplitude modulation of the cosinusoidal force resembles a tube where the friction is high in the middle region, so the amplitude of the fluctuating force decreases but in this case the friction is low at the bottleneck so the amplitude increases.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Plots of the one period of the entropic barrier (solid curve), coupled with the time-varying zero-mean modulated oscillating external force (dotted curve). Dashed curves show the amplitude variations. Total simulation time is selected as one period τ = 2π . Panels (a) and (c) are for F(t) = A sin(t/2) sin(10t); panels (b) and (d) are for F(t) = A cos(t/2) cos(10t). Panels (a) and (b) show the phase shifts between the force and the barrier; panels (c) and (d) show the shifted barrier profiles.

We set a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , k_B = 1, and γ = 1 to determine the entropic barrier geometry and diffusion constant. We carry out a study in three dimensions and set α to be 1/2. Using Simpson’ s integration method, ^[27] we numerically compute the average current given in Eq. (7) and efficiency in Eq. (10) of the Brownian particles under unbiased forces, which are given by Eqs. (11)– (14) in the entropic tube. Time averages are calculated within the interval from t = 0 to t = 2π .

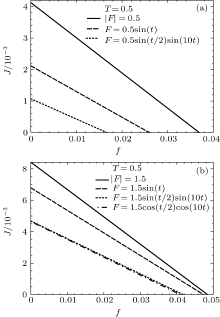
The curves of average current 〈 J〉 versus load f at a constant temperature are plotted for different forces, which are given in Eqs. (11)– (14) with low amplitude A = 0.5 and high amplitude A = 1.5 in Figs. 2(a) and 2(b), respectively. It can be seen from Fig. 2 that the average current at the zero load f = 0 has a maximum value, however it decreases linearly with increasing load f in different force forms. At the critical load value, the current reaches zero, which indicates that the current does not appear in the entropic barrier. Figure 2 clearly also shows that the current in the entropic barrier, which is caused by a temporal force, is bigger than those caused by the oscillating forces. The amplitude of unbiased force plays an important role in the current and critical load values in the entropic barrier at constant temperatures. One can see that the current and critical load values for the high amplitude case (A = 1.5) in Fig. 2(b) have higher values for all types of external unbiased forces than for the low amplitude case (A = 0.5) in Fig. 2(a).

The curves of efficiency η versus load f at constant temperature are plotted for different types of the unbiased forces with low amplitude A = 0.5 and high amplitude A = 1.5 as seen in Figs. 3(a) and 3(b), respectively. It can be seen from Fig. 3 that the efficiency has quite different behavior from the current behavior of Brownian particles in the entropic barrier. At zero load, the efficiencies for all different kinds of forces are all zero. However, the efficiency increases to a maximum value until reaching to the first critical load value and then it smoothly decreases and reaches zero at the second critical load for different forces given in Eqs. (11)– (14) at constant temperatures. This figure clearly shows that there is no direct correlation between current and efficiency for the entropic barrier. It can be seen from Figs. 3(a) and 3(b) that the efficiency behaves differently for the selected different amplitude values. For the low amplitude case in Fig. 3(a), the efficiency takes a maximum value for all different forces and their first and second critical load values are distinct. However, for the high amplitude case in Fig. 3(b), the maximum efficiency of temporal force is lower than that of the oscillating force. Unlike in Fig. 3(a), it can be seen from Fig. 3(b) that for the high amplitude case, the first and second critical load values are almost coincident with each other.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Plots of average particle current J versus load f for A = 0.5 (a), and 1.5 (b) under various types of oscillating forces (low and high amplitude cases). Selected parameters are α = 1/2, a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , and T = 0.5.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Plots of efficiency J versus load f for A = 0.5 (a), and 1.5 (b) under various types of oscillating forces (low and high amplitude case). Selected parameters are α = 1/2, a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , and T = 0.5.

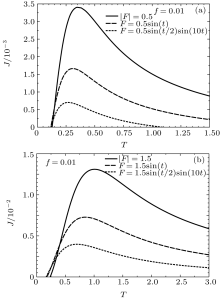
In Figs. 4(a) and 4(b), the curves of average current 〈 J〉 versus temperature at constant load value are plotted for different forces given in Eqs. (11)– (14) for the cases of low amplitude A = 0.5 and high amplitude A = 1.5 respectively. It can be seen from these figures that the current curves have similar characteristic behaviors for different amplitude values. The average positive current under a constant load value appears at a critical temperature value. The current rapidly increases, up to a maximum value as the temperature increases. These maxima due to the dependence on other parameters appear at the second critical temperature value. The current curves smoothly decrease with increasing the temperature. One can obtain higher current values by applying forces with high amplitudes than with low amplitudes. These figures also show that the current caused by an unbiased temporal force is higher than that by oscillating forces. In both figures, average currents are computed for a small load value.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Temperature dependences of the average particle current J for various types of oscillating forces at A = 0.5 (a) and 1.5 (b) (low and high amplitude cases). Selected parameters are α = 1/2, a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , and load f = 0.01.

Temperature dependences of the efficiency are given in Figs. 5(a) and 5(b) for different forces given in Eqs. (11)– (14) with low amplitude A = 0.5 and high amplitude A = 1.5, respectively. The efficiencies of Brownian particles in the entropic tube have the same characteristic behaviors for different amplitude values. Like current, efficiency also appears at the first critical temperature and it rapidly goes to a maximum at the second critical temperature value. Furthermore, these figures show that for the high amplitude case, efficiency takes a higher value above a high temperature value. On the other hand, for the high amplitude case as can be seen from Fig. 5(b), the efficiencies caused by oscillating forces are higher than that caused by a temporal force. This different behavior can also be predicted by considering Fig. 3(b).

In the above figures, we investigated the current and efficiency each as a function of load and temperature. We see that the current and efficiency clearly depend on all parameters of the barrier model and type of unbiased force. However, these figures do not show a certain interval of parameters where current and efficiency are maximum or minimum, instead, they indicate that the amplitudes of all unbiased forces play an important role in the directional transport of Brownian particles in the entropic barrier. Therefore, in order to investigate the effects of the amplitude on the current and efficiency, we study the dependences of the current and efficiency on the amplitude variation under unbiased forces at constant temperature and load values. Amplitude dependences of current and efficiency are given in Figs. 6(a) and 6(b) for different forces. It can be seen from Fig. 6(a) that the current caused by an unbiased temporal force increases up to A = 0.5 and then decreases sharply above A > 0.5. On the contrary, the unbiased oscillating forces are more efficient on the current for the amplitudes in a range of A > 1.0. Here the negative currents in Fig. 6(a) show that the current becomes reversed in the entropic barrier for the chosen parameters.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Temperature dependences of the efficiency η for various types of oscillating forces at A = 0.5 (a) and 1.5 (b) (low and high amplitude cases). Selected parameters are α = 1/2, a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , and load f = 0.01.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Effects of the amplitude of the zero-mean force on the average particle current J (a) and efficiency η (b) for various types of oscillating forces. Selected parameters are α = 1/2, a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , f = 0.01, and T = 0.2.

On the other hand, the efficiencies in Fig. 6(b) also show interesting behaviors similar to the currents in Fig. 6(a), depending on the amplitudes of the forces. It can be seen from Fig. 6(b) that the efficiencies of Brownian particles appear at the first critical A values and they rapidly increase up to other critical A values for all types of unbiased forces. We roughly say that efficiencies have maximum values in an approximately A < 0.5 region. However, in a certain A region, which corresponds to approximately A > 0.5, the efficiencies caused by unbiased oscillating forces take higher values than the efficiency caused by temporal force. Moreover, in the limit of high amplitude, the efficiencies approach to zero under all types of forces. As a result, Figs. 6(a) and 6(b) obviously show that amplitude plays a key role in determining the current and efficiency.

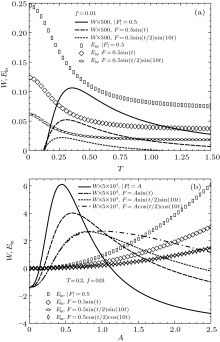
Finally in order to understand efficiency, the variations of average useful work 〈 W〉 in Eq. (8) and mean input energy 〈 E_in〉 in Eq. (9) with temperature and amplitude are given in Figs. 7(a) and 7(b), respectively. As can be seen from Fig. 7(a) that the values of 〈 E_in〉 almost exponentially decay with the increase of temperature for different types of forces at constant load. On the other hand, the values of useful work 〈 W〉 start to increase from the critical temperature T up to maxima for different types of forces at constant load f and then they smoothly decrease with the increase of temperature. This figure clearly shows that the increasing of temperature reduces the energy and increases the useful work of the Brownian particle in a certain temperature interval. In these calculations, 〈 W〉 and 〈 E_in〉 values are calculated for one period of the entropic barrier. The useful work and input energy per unit length can be calculated by dividing them with L = 2π . In Figs. 7(a) and 7(b), 〈 W〉 is scaled by a factor of 500 and 5 × 10⁴, respectively in order to compare it easily with 〈 E_in〉 . The values of input energy 〈 E_in〉 in Fig. 7(b) slowly increase with the increase of amplitude for different types of forces at constant load f and temperature T. The average useful work 〈 W〉 increases with the increase of amplitude, however, it decreases with the increase of the amplitude after passing through the maxima for different types of forces at constant load f and temperature T. The interesting behavior of useful work is that the rates of increase and decrease in the neighborhood of critical amplitude are different.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Variations of useful work 〈 W〉 and input energy 〈 Ein〉 with temperature (a) and amplitude (b) for various types of forces. Selected parameters are α = 1/2, a = 1/2π , b = 1.5/2π , Δ = 1.0, L = 2π , and f = 0.01.

The numerical results given in the above figures support the fact that there is an optimal region in the parameter interval to obtain efficient transportation of the Brownian particles in the entropic barrier under unbiased forces. On the other hand, these results indicate that the current and efficiency under the temporal and different oscillating forces depend on all parameters of the barrier and the applied unbiased forces. One can draw a conclusion that by adjusting the parameters of entropic barrier and the type of force, the intended current or efficiency can be obtained.

In this study, we numerically compute the average currents and efficiencies of the Brownian particles under the temporarily symmetric unbiased force and different forms of sine and cosine forces in an entropic barrier. We show that the current and efficiency of particles appear in an optimal parameter interval. These quantities closely depend on the parameters of the barrier shape and the applied forces. Under a static barrier shape, we see that different force forms give rise to different current and efficiency profiles due to the chosen parameters. The obtained results show that the currents and efficiencies caused by temporal forces take higher values for small amplitudes than by the oscillating forces. However, within an optimal load and temperature interval, the higher efficiencies are obtained under oscillating forces with high amplitudes than under the temporal forces. In addition, we can emphasize that under an oscillating force or a temporal force, higher current does not always correspond to higher efficiency in the presence of an entropic barrier. Mainly this study indicates that an oscillating force can also be used as well as a temporal force in order to produce the current and efficiency for the Brownian particles in a suitable entropic tube profile. Finally it can be concluded that by adjusting the parameters of entropic barriers and applied force, the current or efficiency can be controlled dynamically.