†Corresponding author. E-mail: m-mirzaee@araku.ac.ir
In this paper, we present a structure for obtaining the exact eigenfunctions and eigenvalues of the Jaynes–Cummings model (JCM) without the rotating wave approximation (RWA). We study the evolution of the system in the strong coupling region using the time evolution operator without RWA. The entanglement of the system without RWA is investigated using the Von Neumann entropy as an entanglement measure. It is interesting that in the weak coupling regime, the population of the atomic levels and Von Neumann entropy without RWA model shows a good agreement with the RWA whereas in strong coupling domain, the results of these two models are quite different.
The interaction between a two-level atom and a quantized single mode electromagnetic field is described by the Jaynes– Cummings model (JCM).[1] The JCM is a fascinating model in quantum optics so that it is a solvable model specially with the rotating wave approximation (RWA).[2] The rotating wave approximation is usually employed in the near resonance and in relatively weak atom– cavity coupling.[3] Recently, it has been found applications in quantum information theory, [4– 8] supersymmetric model, [9, 10] some solid state systems, [11– 15] and the LC resonator inductively coupled to a superconducting qubit.[16– 21] However, recent theoretical results indicate that the RWA is essentially challenged within some regions. Therefore the JCM without RWA is the focus of current research interests.[22– 26, 30– 32]
In recent years, several solutions for JCM without RWA have been proposed, such as the Dick model, [25] the Zeno effect, [27, 28] and the tunable extended bosonic coherent states.[29] On the other hand the time evolution of the atomic (field) quantum entropy denotes the degree of the atom– field entanglement so that the higher entropy means the greater entanglement. In this point of view, some authors have investigated the evolution of the entanglement in the JCM without RWA.[33, 34]
In this work we propose a direct solution for the JCM without RWA, then we study the atom– field entanglement using the Von Neumann entropy. The structure of this paper is arranged as follows: In Section 2 we obtain the exact eigenfunctions and eigenvalues of JCM without RWA, then we plot the ground state energy as a function of the atom– cavity coupling constant. In Section 3 the time evolution operator is obtained and the wave function of the system at t > 0 is calculated. Finally, in Section 4 we investigate the time evolution of the Von Neumann entropy as a criterion of entanglement.
In the following, we consider a quantum optical model where a single two-level atom interacts with a single quantized cavity mode of the radiation field. The usual Hamiltonian of the JCM without RWA can be defined as follows (ħ = 1):

where a† and a are the field creation and annihilation operators respectively, ω A and ω F are the frequencies of the atom and cavity, g is the atom– cavity coupling constant and σ k (k = x, y, z) is the Pauli matrix of a two-level atom. For convenience we can write a transformed Hamiltonian with a rotation around the y axis by an angle π /2 as the following form
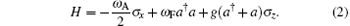
Considering this Hamiltonian, there is a commutative conserved parity Π with Hamiltonian such that [H, Π ] = 0, which is given by
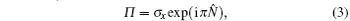
where 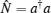
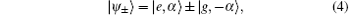
where | e〉 and | g〉 denote the excited and the ground states of the atom respectively, and α is the coherent state of field,

Since [H, Π ] = 0 the vectors in Eq. (4) are eigenfunctions of Hamiltonian (2) too. For measuring the eigenvalues of Eq. (2), if we can substitute Eq. (2) into the Schrö dinger equation H| ψ ± 〉 = E± | ψ ± 〉 , we obtain

Multiplying both sides of Eq. (5) by 〈 α | ⊗ , we can write
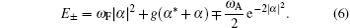
Now we try to obtain the ground state energy (GSE) by using equation
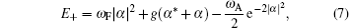
which is smaller than other energy E− in Eq. (6) as a function of g. To carry out this, we find the minimum value of the energy E+ as follows: After differentiating with respect to α and equating zero, one can obtain g value as follows:
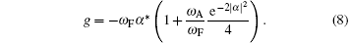
By solving Eq. (8) for α relative to g and substituting it into Eq. (7) we can plot GSE for different ratios of ω A/ω F relative to g in Fig. 1.
It is interesting that the GSE shows similar behavior in different ratios of ω A/ω F but with increasing the ratio of ω A/ω F the GSE becomes more negative in g = 0, so that for ω A/ω F = 0.5, 1, 1.5, the GSE values start approximately from − 0.28, − 0.5, and − 0.76 respectively. It is interesting that the obtained results of these diagrams are identical with those of Ref. [29].
In the interaction picture the Hamiltonian (1) takes the form

where Δ is the atom– field detuning parameter (Δ = ω A − ω F). Now the Hamiltonian Eq. (9) in the atomic basis can be given as follows:
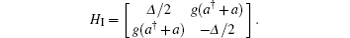
Using the relation 
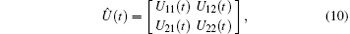
where
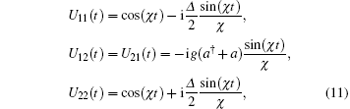
and
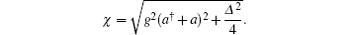
In the following discussion, we consider a quantum optical model where a single two-level atom interacts with a single quantized cavity mode of the radiation field. In the case that if the atom is initially in the excited state | e〉 and the field is also in the pure state | ψ F(0)〉 , the initial atom– field total system is given by
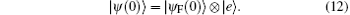
At t = 0 the field– atom system is in a pure state, thus the initial density operator of the system is described by ρ (0) which is given by ρ (0) = | ψ F(0)〉 〈 ψ F(0)| ⊗ | e〉 〈 e| . Now we obtain the time evolution of the wave function (12) at t > 0 as
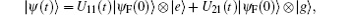
where the operators Uij(t) are given by Eq. (11). So for the resonance case (i.e., for Δ = 0) we obtain
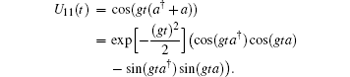
If the cavity field is initially prepared in the coherent state | ψ F(0)〉 = | α 〉 , we have
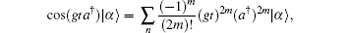
where
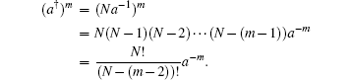
Also using the following relations
we can get the time evolution of the wave function as
In Eq. (13) coefficients are given by

It is well known that the total density matrix ρ (t) = | ψ (t)〉 〈 ψ (t)| has all information about the system. On the other hand the atomic reduced density matrix ρ A(t) for the wave function (13) can be written via the relation

where
and
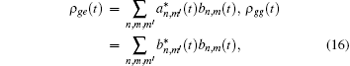
which coefficients ai, bj are given in Eqs. (14).
The Von Neumann entropy is a very useful measure of the purity of the quantum mechanical state and also is a degree of the entanglement of the atom– field interaction. The Von Neumann entropy of a quantum mechanical system can be defined as
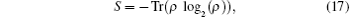
where ρ is the density operator of the quantum system. In a pure state the Von Neumann entropy is equal to zero and for a mixed state S > 0. Quantum entropies of the field and the atomic subsystems are defined through the corresponding reduced density operators
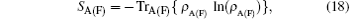
the reduced density operators ρ A(F) are defined by ρ A(F) = TrF(A)ρ . On the other hand, using the diagonal form of the density operator, entropy may be written as
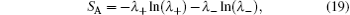
where λ ± are the eigenvalues of the atomic reduced density operator ρ A.
Figures. 2(a)– 2(c) show the time evolution of the entropy (19) for initial state | ψ F(0)〉 = | α 〉 ⊗ | e〉 for g = 0.01, 0.1, and 1 respectively. It is interesting that in the small values of g for example g = 0.01 the diagram of the case without the RWA model is approximately similar to that with the RWA model, see Fig. 3(a), so that for small values of g the RWA can be employed. With increasing value of g, for example in g = 0.1 we observe some different behavior. According to Fig. 3(b) for JCM with the RWA model, entanglement increases at t > 10 whereas it remains constant according to the case without the RWA model (Fig. 2(b)). In g = 1 the diagrams in comparison with both models (Fig. 2(c) and Fig. 3(c)) are obviously different. In Fig. 3(c) around times t = 0, 15, 31, and 47 s entropy has value 0.5 and shows more fluctuation between these times, but in Fig. 2(c) entropy has less oscillations around these times and takes a constant value ‘ 0.5’ in these time durations.
 | Fig. 2. The Von Neumann entropy as a function of time for JCM without RWA for (a) g = 0.01, (b) 0.1, and (c) 1. |
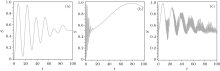 | Fig. 3. The Von Neumann entropy as a function of time for JCM with RWA for (a) g = 0.01, (b) 0.1, and (c) 1. |
Figures 4(a)– 4(c) show the population inversion of atomic levels for the case without the RWA model and figures 5(a)– 5(c) show the results of the population inversion with the RWA model, for various values of g. Looking carefully at these figures we discover that figure (4(a) is similar to Fig. 5(a), as Figs. 2(a) and 3(a), for lower values of g (g = 0.01), the cases without the RWA model and with the RWA model show similar behavior for low duration of time, but their behavior for larger times becomes calmly different, figure 6 shows this comparison.
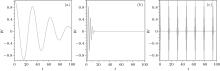 | Fig. 4. The population inversion of atomic levels (W = ρ ee– ρ gg) as a function of time for JCM without RWA for (a) g = 0.01, (b) 0.1, and (c) 1. |
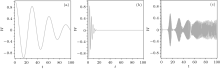 | Fig. 5. The plot of the population inversion of atomic levels (W = ρ ee– ρ gg) versus time for JCM with RWA (a) g = 0.01, (b) g = 0.1, and (c) 1. |
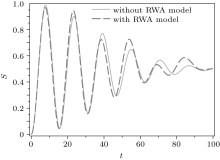 | Fig. 6. The comparison of the Von Neumann entropy with and without RWA as a function of time at g = 0.01. |
This is due to the fact that the entropy and the population inversion depend on the product of g and t, so that for lower values of g and t this product is low and the two models show similar behavior but at larger times the product (gt) becomes large and their behavior is different, this result is also exhibited in the case of the population inversion (Fig. 7).
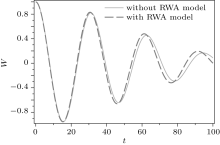 | Fig. 7. The comparison of the population inversion for the cases with the RWA model and without the RWA model as a function of time at g = 0.01. |
In Figs. 4(b) and 5(b) the population inversion up to t = 20 s shows fluctuation behavior but for t > 20 s it remains constant W = 0. As we know, the population inversion of atomic levels in coherent state shows the collapse– revival behavior and it is clear that the case without the RWA model shows this behavior better than that with the RWA model. On the other hand for lower values of g there is not enough time to observe this phenomenon. From the above discussion, it follows that for lower values of g, we can employ the RWA, but with increasing values of g, this approximation cannot be employed.
In summary, we have solved the Hamiltonian of the JCM without RWA and obtained exact eigenfunctions and eigenvalues. The GSE reduces with increasing g and the behavior of this decreasing is in good agreement with Ref. [29]. Based on the time evolution operator, we are able to calculate exactly the entanglement evolution of the JCM system (atom– field) without RWA. The results are essentially different from RWA cases in the strong coupling regime. Also we have investigated the atom– field entanglement without RWA using the Von Neumann entropy. It was observed that for small values of g, the results of entanglement without RWA model are very similar to that of entanglement with RWA. The behavior of the atom– field entanglement without RWA was completly different from entanglement with RWA in larger values of g.
We wish to thank Dr. A. Zendehnam for his careful reading the article and for his constructive commends.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|



