Quantum state transfer (QST) between two remote parties is an essential ingredient of scalable quantum information processing. Quantum channels enabling universal operations between two physically separated registers have been proposed in a variety of quantum systems, including superconducting transmission lines, ^[1] Coulomb coupling trapped ions, ^[2] and optical photons.^{[3, 4]} Multi-mode entangled photon states, which are useful for quantum networks, can be generated efficiently using an integrated photonic circuit.^[5] In particular, coupled quantum spin systems have attracted much attention for short distance quantum communication in recent decades.^{[6– 16]} Such coupled-spin quantum channels provide an interesting alternative to direct register interactions and interfacing with photonic flying qubits. For this reason, most of the feasible proposals have been proposed for perfect QST, in which the quantum channels commonly rely upon engineered couplings entailing suitable dispersion relations, ^{[17– 20]} weak couplings undergoing an effective Rabi oscillation or a ballistic regime, ^{[21– 24]} and dynamical manipulation.^{[25– 28]}

In contrast to two-dimensional quantum systems, high-dimensional quantum systems serving as qudits have been extensively studied due to their key advantages in large capacity and high security. While such advantages have been explored in quantum communications ranging from quantum key distribution to quantum teleportation, ^{[29– 39]} qudit systems are also candidates for quantum computation ranging from universal quantum simulations and asymptotically optimal quantum circuits to one-way quantum computation and fault-tolerant quantum computation.^{[40– 53]} Indeed, several high-dimensional QST protocols have been presented in coupled-spin chains.^{[54– 57]}

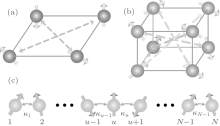
Similar to classical supercomputers involving parallel processing, ^[58] hypercube topology can potentially allow diverse applications in QST, ^{[17, 59– 61]} quantum random walks^{[62– 65]} and quantum search algorithms.^{[66– 69]} A hypercube is a generalization from a three-dimensional cube to a high-dimensional configuration, and it possesses many appealing topological features, e.g., node-symmetry, good balance between nodes and edges.^[58] Prior state transfer schemes in hypercubes have focused on qubits using either spins, ^[17] single-photons, ^[60] or multiphoton states.^[61] In this article, we propose an efficient high-dimensional QST in XX coupling spin hypercube networks. The hypercubes are multiple Cartesian products of a chain of either two or three spins, which works as building blocks of these topologies.^[70] Upon performing free spin wave approximation, unitary evolution for a specific time results in a perfect high-dimensional swap gate and evolution time is independent of either the distance between two registers or the dimension of the sent state.^[61] It require neither weak coupling nor projective measurement nor external modulation nor coupling engineering. In addition, utilizing the Schwinger picture yields a perfect mirror high-dimensional swap operation in a coupled-spin chain of arbitrary length. Numerical results confirm that the spin-wave interaction leads to the leakage of quantum information, and under the free spin wave approximation, the perfect high-dimensional QST is achieved.

The proposed efficient high-dimensional QST occurs in a closed quantum channel. However, a quantum channel can rarely be isolated from its surrounding environment, especially the spin bath. Thus it is necessary to discuss the decoherence effects on such protocols. The considered decoherence is characterized by a pure dephasing model for quantum channels coupled to an antiferromagnetic (AFM) spin bath via a typical Ising interaction, ^{[71– 76]} allowing for the conservation of channel energy. In a low temperature regime, unitary evolution analytically gives a swap gate experiencing decoherence. To be specific, we perform numerical simulations when the spin bath is in a thermal equilibrium state. We find that while increasing either the spin bath temperature or the bath-channel coupling enhances the irreversible leakage of quantum information into the spin bath, strong intrachannel coupling can depress the decoherence effects to ensure the high fidelity of state transfer. Observing these can help us to understand the decoherence effects on quantum communication in coupled quantum spin systems.

The rest of this paper is organized as follows. In Section 2, we calculate the Hamiltonian and the operator evolution under free spin wave approximation. In Section 3, we study the high-dimensional QST in hypercubes and chains, respectively. In Section 4, specifically, the decoherence of the spin bath in the thermal equilibrium state is studied. The last section is devoted to a summary.

The composite system under consideration consists of a quantum spin-S₀ network which acts as a quantum channel, and an AFM spin-S bath whose lattice is divided into two identical sublattices a and b. The network Hamiltonian with spins coupled to their nearest neighbors on a finite lattice of site N₀ is of XX coupling

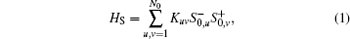
where K is an N₀ × N₀ coupling matrix and K_uv represents the coupling strength between sites u and v, S^± = S^x ± iS^y are two ladder operators and S^μ (μ = x, y, z) is the μ component of a spin operator S. The AFM spin bath Hamiltonian is described by a Heisenberg model

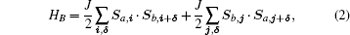
where J > 0 is the exchange interaction, δ is a vector joining a site to its nearest neighbor, S_a and S_b are spin operators in the sublattices a and b, respectively. The interaction Hamiltonian between the network and the spin bath is characterized by a typical Ising model^[73]

with the coupling strength J₀ and the number of spins N in each magnetic sublattice. The dynamics of a composite system is governed by the total Hamiltonian H = H_S + H_B + H_I, and upon introducing the Holstein– Primakoff (HP) transformation, ^[77] we have

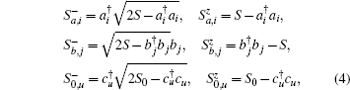
the total Hamiltonian can be expressed in terms of boson operators, wherein the conservation of total spin z projection of channel, , becomes conservation of the boson number, .

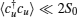
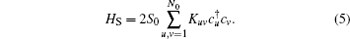
The network is initialized to a simple ferromagnetic order with spins aligning in a parallel way. The low-lying level states of a sender, ranging from |0〉 to |d – 1〉 , are employed to encode quantum information as an input state, and we assume that the dimension d of the sent state is much smaller than 2S₀, d ≪ 2S₀. The conservation law ensures that , and the HP transformation is simplified into , which leads to

The subsequent diagonalization of this tight-binding Hamiltonian is realized through an orthogonal transformation Q, such that Λ = QKQ^† with Λ _qq′ = λ _qδ _qq′ . This transformation results in 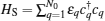, where and ε _q = 2S₀λ _q.

The spin bath surrounding the quantum channel is in the low-temperature and low-excitation limit such that the spin operators can be approximated as and .^[78] Working with Fourier transformation and Bogoliubov transformation yields

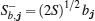
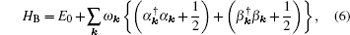
where α _k and β _k are two degenerate AFM mangnon branches, and E₀ = – z₀JNS(S + 1). The spin-wave elementary excitation spectrum (EES) is

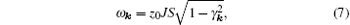
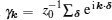
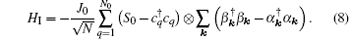
wherein z₀ is the number of the nearest neighbors, and is the structure factor. In the low-energy regime, corresponding to long wavelengths, k ≪ l, the EES is linear: ω _k = (2z₀)^1/2JSkl, with the lattice constant l. The interaction Hamiltonian is likewise transformed to

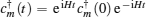
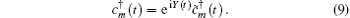
The Heisenberg equation drives an operator evolution in the Heisenberg picture, . By using this equation and the commutation relation [H_I, H] = 0, we have

Here, the quantum noise operator Y (t) reads

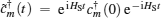
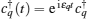
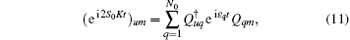
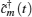
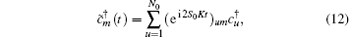
which arises from the AFM spin bath, and is the free evolution of the network. Owing to , and

turns out to be

and the free evolution of the network is determined by its coupling matrix.

In this section, high-dimensional QST protocols with high fidelity in hypercubes and chains are proposed, respectively. We begin with the case of hypercubes, which are multiple Cartesian products of either two-spin chain G₁ or three-spin chain G₂ working as basic building blocks to build such coupled-spin hypercubes. The coupling matrix of a hypercube network G in Eq. (1) is K = κ A (G), and κ is the coupling strength between two spins in the network, which is characterized by its adjacency matrix A (G).^[70]

After g-fold Cartesian products of either of the two simple chains, A (G) is given by

where I is an identity matrix, and A (G_θ ) is an adjacency matrix of G_θ for θ = 1, 2. As a consequence,

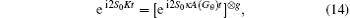
and it results in

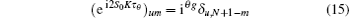
at the following evolution time

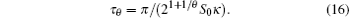
Substituting Eq. (15) into Eq. (12) leads to

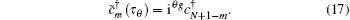
Upon absorbing a phase factor of i^{θ _g} into , unitary evolution under H_S for a time τ _θ results in , which allows the realization of a swap operation between two spins m and N + 1 – m. It is determined by the natural dynamics of the Hamiltonian and requires neither external modulation nor inter-spin coupling strength engineering. Moreover, the evolution time is independent of the distance between the two remote spins, and the speedup of perfect high-dimensional QST is possible. For simplicity, we take the square and cube networks for example, as shown in Figs. 1(a) and 1(b), which are the two-fold and three-fold Cartesian products of G₁, respectively; the time evolution builds a swap gate between two spins along each main diagonal at the optimal time.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Schematic configurations for two-fold (a) and three-fold (b) Cartesian products of a two-spin chain with uniform coupling strength κ . Unitary evolution for a time τ 1 = π /(4S0κ ) results in a high-dimensional swap operation between two spins along each main diagonal. In a coupled-spin chain of length N (c), unitary evolution for a time τ ′ = π /(2S0g0) enables a mirror-like high-dimensional swap operation with respect to its center through engineering inter-spin coupling strengths .

While the case of a multi-dimensional hypercube has been chosen to focus on, we extend such results to a one-dimensional coupled-spin system. By choosing

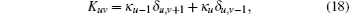
in the Hamiltonian of Eq. (1), such that it provides a Hamiltonian of a coupled-spin chain with coupling strengths κ _u between two spins u and u + 1 as shown in Fig. 1(c). The coupling matrix is identical to a pseudo Hamiltonian H′ = g₀L_x, where L_x is the x component of a fictitious spin L = (N₀ – 1)/2, and g₀ is a coupling parameter. In the Schwinger picture, L_x can be rewritten in terms of two boson operators as^[79]

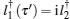
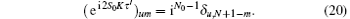
and hence, H′ is the Hamiltonian governing two bosons with coupling strength g₀/2. Unitary evolution under 2S₀H′ for a time τ ′ = π /(2S₀g₀) gives and , yielding

Therefore, is evaluated to be

Upon absorbing a factor of i^{N₀ − 1} into as desired, it enables a swap operation between spins m and N₀ + 1 – m, , and a mirror inversion of quantum states with respect to the center of the chain is implemented.

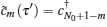
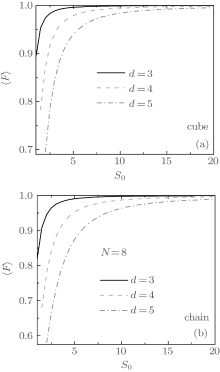
To confirm the perfect high-dimensional QST, we perform a numerical calculation, as shown in Fig. 2. The initial state of the network is assumed to be

where

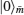
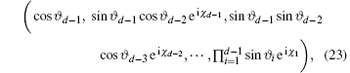
is the sent state at the spin m, and represents that all spins are in the vacuum state apart from just one spin at the site m. The normalized coefficients C_ν can be measured by the Hurwitz parametrization with d – 1 polar angles χ _p and d – 1 azimuthal angles ϑ _p as^{[80, 81]}

where 0 ≤ ϑ _p ≤ π /2 and 0 ≤ χ _p < 2π for p = 1, 2, … , d – 1. The average fidelity over the whole manifold of such states is

Here, F (t) is defined as F (t) = ₁ 〈 φ | ρ m (t) | φ 〉 ₁ with ρ m (t) being the reduced density matrix of spin m at the evolution time t. The volume element on the generalized Bloch sphere of Eq. (23) in the complex space CP^{d– 1} is

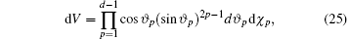
and the total volume of the 2(d – 1)-dimensional manifold of pure states is V_d = π ^{d – 1}/(d – 1).

The average fidelity varies with spin number S₀ as shown in Fig. 2. The infidelity, ε = 1 – 〈 F〉 , results from the leakage of quantum information into the spin wave interaction found in nonlinear terms of HP transformation. In such a regime 2S₀ ∼ d, the evolution of the quantum channel is dominated by the spin wave interaction suppressing the average fidelity. By ensuring 2S₀/d ≪ 1, the spin wave interaction is negligible and the evolution is governed by the free spin wave found in linear terms of HP transformation, enabling a perfect high-dimensional QST.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Variations of average fidelity 〈 F〉 with quantum spin number for either d = 3 (solid lines), d = 4 (dashed lines), or d = 5 (dotted– dashed lines). (a) Coupled-spin cube; (b) coupled-spin chain of length N = 8. Here, the evolution time is the optimal time for the two different configurations.

To be specific, we consider a spin bath in a thermal equilibrium state, wherein its variables are distributed in an uncorrelated thermal equilibrium mixture of states, and the density matrix satisfies the Boltzmann distribution

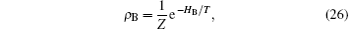
where Z = Tr(e^{− H_B/T}) is a partial function and T represents the temperature. The combination of Eq. (26) and Eq. (22) yields the initial state of the composite system, including quantum channel and spin bath, as a direct product

Evolution for time τ ′ drives the state to

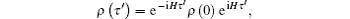
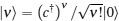
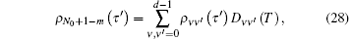
and the reduced density matrix of the quantum channel is ρ S (τ ′ ) = Tr_B [ρ (τ ′ )]. Without loss of generality, we choose a couple-spin chain, which is directly analogous to the hypercube quantum channel. Upon utilizing and e^{− iHτ ′} c^† (0) e^{iHτ ′} = c^† (− τ ′ ), the finial state of spin N₀ + 1 – m is calculated as

with 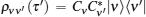, and a decoherence factor D_vv′ (T) given by

which turns out to be . Therein,

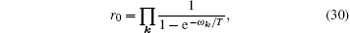
and

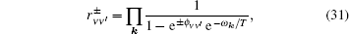
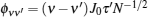
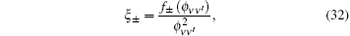
where . Upon introducing quantities

and

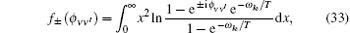
with x = kl, the decoherence factor is transformed to

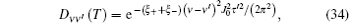
where the summation over k has been replaced by an integral

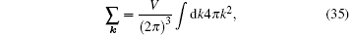
with N = V/l³. In the thermodynamic limit, N → ∞ , which leads to ξ ₀ = ξ ± , and

Thus the decoherence factor becomes

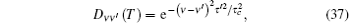
with a decoherence time

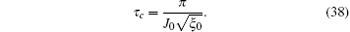
The combination of the fidelities of spins m and N₀ + 1 – m is

To illustrate the decoherence effects of spin bath on the quantum channels, we perform the numerical simulation as shown in Fig. 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Decoherence effects on the high-dimensional QST proposal in a coupled-spin chain with either d = 3 (solid lines), or d = 5 (dotted– dashed lines). The average fidelity as functions of (a) J0 with g0 = J and T = 0.05TN, (b) T with g0 = J and S = 1/2, and (c) g0 with J0 = 5000J and S = 1/2.

Under the random phase approximation, the Né el temperature of an AFM system reads^[78]

with ζ = N^{− 1}∑ _k(1 − γ _k)^{− 1}. The summation over k is restricted in the first Brillouin zone of the sublattice, such that it has half the volume of an atomic Brillouin zone, yielding ζ = 1.51638 for a simple cubic lattice and ζ = 1.39320 for a body-center cubic lattice. Owing to the validity of spin wave theory only in the low temperature regime, the spin bath temperature is restricted below 0.1T_N, T ≤ 0.1T_N. The average fidelity varies with either coupling strength, J₀, or spin bath temperature, T, as shown in Figs. 3(a) and 3(b). The infidelity, ε , results from the leakage of quantum information into the spin bath. Increasing either J₀ or T enhances such an irreversible process. Figure 3(c) shows the variations of average fidelity with coupling parameter, g₀. A strong coupling parameter can partly counteract the thermal effects to prevent the quantum information from leaking into the spin bath and ensure the high fidelity.

In this paper, we study a high-dimensional QST protocol in spin networks of either hypercubes or chains coupled to an antiferromagentic spin bath. Under the free spin wave approximation and in ideal conditions without decoherence, the time evolution presents a perfect high-dimensional QST between two registers of arbitrary distance for both of the two configurations, requiring neither weak coupling nor external modulation nor projective measurement. The essence of our method is that a perfect swap operation is allowable for a chain of either two or three bosons. One of its direct applications is that it can potentially provide the high-dimensional entanglement distribution for quantum computation. Moreover, the state transfer independent of either the distance between two registers or the dimension of sent state enables the enhancement of computational efficiency. In the low temperature regime and thermodynamic limit, the decoherence induced by the AFM spin bath is also investigated in this work. Increasing either the spin bath temperature or the channel-bath coupling, the decoherence becomes more serious. However, strong intrachannel coupling can partly counteract the decoherence effects, and ensure the high fidelity to demonstrate robustness against external noise. Observing these will deepen our understanding of the decoherence effects on quantum communication in the coupled quantum spin systems.

While we have focused on the specific case of a hypercube topology, the conceptual framework can be used in a wide range of topologies by means of the free spin wave approximation to yield the tight-binding Hamiltonian described in Eq. (5). By ensuring (e^i2S₀Kτ )um = δ _{u, N0+ 1− m} for a specific evolution time τ , the achievement of a perfect high-dimensional QST is possible.